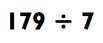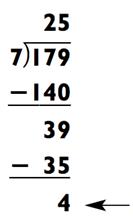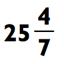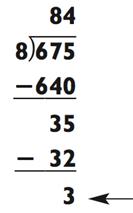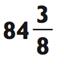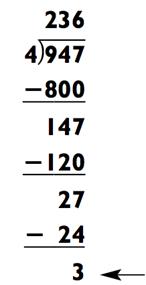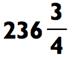Деление в уме - чрезвычайно полезный навык, как для бизнеса, так и для быта. Сколько раз в неделю вы сталкиваетесь с ситуациями, которые требуют от вас равного разделения чего-либо, например, счёта в ресторане? Точно такой же навык бывает весьма кстати, когда вы хотите выяснить стоимость за одну упаковку корма для собак или поделить выигрыш во время игры в покер, или узнать, сколько литров бензина вы можете купить на $20. Способность делить в уме может спасти вас от неудобства в виде постоянного обращения к калькулятору, когда вам нужно посчитать что-либо.
В рамках устного деления, метод вычисления слева направо вступает в свои права. Это тот самый метод, которому нас учили в школе, так что вы будете заниматься естественным для вас делом. Я помню, будучи ребёнком, что думал, будто этот метод деления слева направо олицетворяет то, какой арифметика должна быть в принципе. Я часто размышлял о том, что если бы в школе нашли способ преподавать и деление справа налево, они, вероятно, так бы и сделали!
Деление чисел, состоящих из одной цифры
|
Чтобы решить 179 ÷ 7, мы пытаемся найти число Q, такое, что 7 раз по Q будет 179. Сейчас, так как 179 находится между 7 х 10 = 70 и 7 х 100 = 700, Q должно находиться между 10 и 100. Это означает, что наш ответ является двузначным числом. Зная это, мы сперва определяем наибольшее кратное 10, которое может быть умножено на 7 и в итоге быть меньше 179. Нам известно, что 7 х 20 = 140 и 7 х 30 = 210, значит наш ответ где-то в районе 20>. Отталкиваясь от этого, мы уже можем реально проговорить число «20», так как это будет часть нашего ответа, которая определённо не изменится. Далее мы вычитаем 179 - 140 =
39. Наша задача только что была сведена к задачке на деление 39 ÷ 7. Так как 7 х 5 = 35, что на 4 дальше 39, у нас появилась вторая часть ответа под названием «5» с остатком 4, или, если вы предпочитаете, 25 и 4/7 Вот как выглядит данный процесс:
|
|
Давайте попробуем решить похожую задачку на деление, используя такие же расчёты:
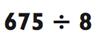
Как и прежде, раз уж 675 находится между 8 х 10 = 80 и 8 х 100 = 800, то ваш ответ должен быть меньше 100 и, следовательно, двузначным числом. Чтобы произвести деление, учтите, что 8 х 80 = 640 и 8 х 90 = 720. Отсюда, ваш ответ в районе 80 «с хвостиком». Но каким хвостиком? Чтобы это узнать, вычтите 640 из 675 для получения остатка в размере 35. После произнесения вами «80», наша задача была сведена к 35 ÷ 8. Так как 8 х 4 = 32, итоговый ответ будет 84 с остатком 3 или 84 и 3/8. Проиллюстрируем данный пример следующим образом:
|
|
Как и большинство устных вычислений, деление может рассматриваться как процесс упрощения. Чем больше вы подсчитываете, тем проще проблема становится. То, что начиналось как 675/8 было сведено к меньшей задаче 35 ÷ 8.
Теперь давайте апробируем задачку, решение которой выльется в трёхзначный ответ:
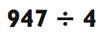
На этот раз, ваш ответ будет содержать три цифры, потому что 947 находится между 4 х 100 = 400 и 4 х 1000 = 4000. С тех пор как нам надо отыскать наибольшее кратное 100, которое может быть сжато до размера 947. Так как 4 х 200 = 800, наш ответ определённо будет 200>, так что вперёд, произнесите это! Вычитание 800 из 947 преподносит нам новую задачку на деление 147 ÷ 4. Так как 4 х 30 = 120, мы можем теперь уже произнести «30». После вычитания 120 из 147, мы рассчитываем 27 ÷ 4 для получения остальной части ответа: 6 с остатком 3. В совокупности мы имеем 236 с остатком 3 или 2363/4.
|
|
Процесс деления четырёхзначного числа на одну цифру такой же простой, как и в следующем примере:
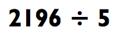
Здесь ответ будет исчисляться сотнями, потому что 2196
находится между 5 х 100 = 500 и 5 х 1000 = 5000. После вычитания 5 х
400 = 2000, мы можем произнести «400», и наша задача будет уменьшена до 196 ÷ 5, что может быть решено по мотивам прошлых примеров.
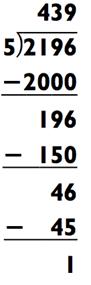
ОТВЕТ: 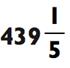
На самом деле, существует куда более лёгкий способ решения последней задачи. Мы можем упростить её путём удвоения обоих чисел. Так как 2196 х 2 = 4392, то мы имеем 2196 ÷ 5 = 4392 ÷ 10 = 439,2 или 439 и 2/10. Мы рассмотрим больше возможностей «срезать» при делении в следующем разделе.
Дата: 2018-12-21, просмотров: 379.