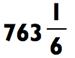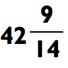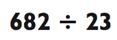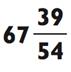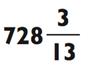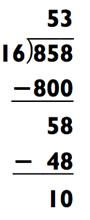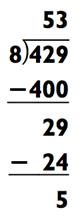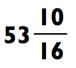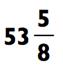
Правило большого пальца
Когда вы делите в уме, а не на бумаге, то вам может показаться сложным запоминание частей ответа, в то время как вы продолжаете вычислять. Один из вариантов, как вы видели ранее, проговаривать ответ вслух по ходу решения. Но для большего драматизма вы можете предпочесть, как и я, удерживать ответ в памяти с помощью пальцев и произносить его целиком в самом конце. В таком случае, вы можете столкнуться с проблемой при запоминании чисел, которые больше пяти, ведь, как и большинство из нас, вы располагаете лишь пятью пальцами на каждой руке. Решением является специальная техника, в основе которой язык жестов. Я называю её «Правило большого пальца». Она наиболее эффективна для запопинания чисел, состоящих из трёх и более цифр. Эта техника полезна не только в данной Главе, но также пригодиться и в последующих, где придётся иметь дело с задачками побольше и с числами подлиннее.
Вы уже знаете, что для представления чисел от 0 до 5, всё, что вам нужно сделать, это поднять эквивалентное количество пальцев на руке. Когда ваш большой палец вовлечён в процесс, лёгким становится представление чисел от 6 до 9. Вот список правил большого пальца:
Чтобы задать 6, разместите большой палец на верхней части вашего мизинца.
Чтобы задать 7, поместите большой палец на верхней части безымянного пальца.
Чтобы задать 8, поместите большой палец на верхней части среднего пальца.
Чтобы задать 9, поместите большой палец на верхней части указательного пальца.
При работе с трёхзначным числом, задайте цифры для сотен на левой руке и цифры для десятков на правой. Когда дело дойдёт до одной цифры, вы достигните конечной точки решения (за исключением возможного остатка). Теперь произнесите число на вашей левой руке, число на вашей правой руке, последнюю цифру, которую только что посчитали, и остаток (что у вас в голове). Вуаля - вы произнесли ответ!
В целях практики попробуйте решить следующую задачку на деление четырёхзначного числа:
|
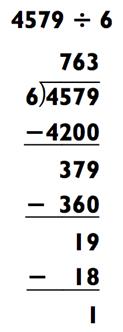
Используя правило большого пальца для запоминания ответа, вы зададите 7 на вашей левой руке, путём соединения большого пальца с безымянным, и зададите 6 на вашей правой руке с помощью соединения большого пальца с мизинцем. Как только вы вычислите последнюю цифру (которая равна 3) и остаток (который равен 1), вы
можете «зачитать» итоговый ответ с ваших рук слева направо: «семь…
шесть…три с остатком один, или одна шестая.»
Некоторые задачи на деление четырёхзначных цифр дают четырёхзначный ответ. В таком случае, раз уж у вас только две руки, вы будете вынуждены вслух произнести цифру для тысячи и использовать правило большого пальца для запоминания остального ответа. Например:
|
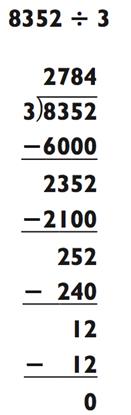
Для решения этой задачи, вы делите 8 на 3, чтобы получить цифру для тысячи в виде 2; произносите «две тысячи» вслух, затем делите 2352 на 3 привычным способом.
Деление на двузначные числа
К данному разделу мы подходим с предположением, что вы уже освоили искусство деления на одну цифру. Естественно, задачи на деление становятся сложнее с увеличением делителя. К счастью, я припас немного магии в рукаве, чтобы сделать вашу жизнь легче.
Давайте начнем с относительно легкой задачи:
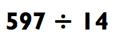
Так как 597 находится между 14 х 10 и 14 х 100, ответ (так же называемый как «частное») будет находится между 10 и 100. Чтобы определить ответ, вам в первую очередь нужно задаться вопросом:
«Сколько раз по 14 даст в сумме 590?» Потому что 14 х 40 = 560, вы будете знать, что ответ находится в районе 40>, так что вы можете произнести «сорок» вслух.
Далее, вычитаем 560 из 597, что даёт нам 37 и сводит задачу к делению 37 на 14. Так как 14 х 2 = 28, ваш ответ 42. Вычитая 28 из 37, мы получаем остаток 9. Процесс выведения решения задачи может быть показан на рисунке следующим образом:
|
|
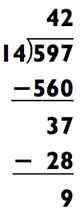
В данном примере ответ будет двузначным числом, так как 682 находится между 23 х 10 = 230 и 23 х 100 = 2300. Чтобы найти цифру для десятка двузначного числа, вам нужно спросить себя: «Сколько раз по 23 даст в сумме 680?» Если вы попробуете 30, то увидите, что это слегка перебор, так как 23 х 30 = 690. Теперь вы в курсе, что ответ находится в районе 20>, и вы можете произнести это. После вычтите 23 х 20 = 460 из 682 для получения 222. Так как 23 х 9 = 207, ответ
будет 29 с остатком 222 - 207 = 15.
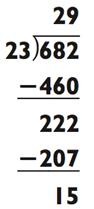
ОТВЕТ: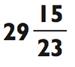 
Теперь рассмотрим:
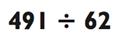
Так как 491 меньше, чем 62 х 10 = 620, ваш ответ будет просто цифрой с остатком. Вы можете попробовать угадать 8, но 62 х 8 = 496,
а это немножко больше. Так как 62 х 7 = 434, ответ будет 7 с остатком
491 - 434 = 57 или 7 и 57/62. 
ОТВЕТ: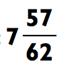 
В действительности, есть отличный трюк, который может облегчить решение таких задач. Помните, как вы сначала пытались перемножить 62 х 8, но обнаружили, что это больше, чем нужно? Ну, это было не напрасно. Помимо информации о том, что ответ будет 7, вы также можете сразу определить остаток. Так как 496 на 5 больше, чем 491, остаток будет на 5 меньше, чем 62, делитель. Раз уж 62 - 5 = 57, то ваш ответ 7 и 57/62. Причина, по которой данный трикс работает, в том, что 491 = (62 х 8) - 5 = 62 х (7 + 1) - 5 = (62 х 7 + 62) - 5 = (62 х 7) + (62 - 5) = 62 х 7 + 57.
Теперь попробуйте посчитать 380 ÷ 39, используя «срезку»,
которую только что выучили. Итак, 39 х 10 = 390, что больше на
10. Следовательно, ответ будет 9 с остатком 39 - 10 = 29.
Следующий вызов для вас - деление четырёхзначного числа на двузначное:
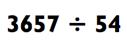
Так как 54 х 100 = 5400, вы знаете, что ваш ответ будет двузначным числом. Чтобы получить первую цифру ответа, вам необходимо выяснить, сколько раз по 54 даст в сумме 3657. Так как 54 х 70 = 3789 (это немножко больше), вы будете знать, что ответ где-то в районе 60>.
Далее, умножьте 54 х 60 = 3240 и вычтите 3657 - 3240 = 417.
Как только вы произнесёте 60, ваша задача будет упрощена до
417 ÷ 54. Раз уж 54 х 8 = 432 (что тоже слегка больше), ваша последняя цифра будет 7 с остатком 54 - 15 = 39.
|
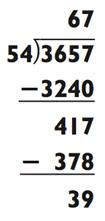
Теперь попробуйте свои силы на задачке с трёхзначным частным:
|
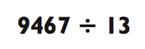
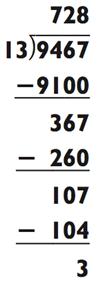
Упрощае м задачи на деление
Если к этому моменты вы страдаете мозгового перенапряжения, расслабьтесь. Как и было обещано, я хочу поделиться с вами несколькими приёмами для упрощения определённых задач на деление в уме. Эти приёмы основаны на принципе деления обоих частей задачи на общий множитель. Если оба числа в задаче чётные, вы можете вдвойне упростить проблему путём деления каждого числа на 2 перед тем как начать. Например, 858 ÷ 16 содержит два чётных числа, и деление их на 2 ведёт к значительно более простой задаче 429 ÷ 8:
|
|
|
|
Как вы сами видите, остатки 10 и 5 отличаются; но если вы запишите остаток в форме дроби, то получите 10/16, что и есть 5/8. Следовательно, используя данный метод, вы всегда должны выражать ответ в форме дроби.
Мы проделали оба типа вычислений для того, чтобы вы увидели, насколько это легче. Теперь ваша очередь практиковаться:
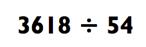
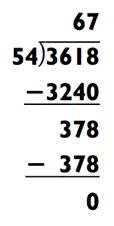РАЗДЕЛИМ НА 2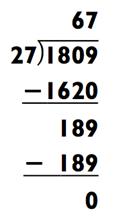 
ОТВЕТ: 67
Пример справа намного легче решить в уме. Если вы очень встревожены, то можете разделить обе части исходной задачи на 18 для получения ещё более простой задачи: 201 ÷ 3 = 67.
Выжидайте задачки, которые можно подвергнуть делению на 2
дважды, такие как:
Мне всегда кажется, что проще дважды разделить проблему на 2, чем делить каждое из чисел на 4. А теперь, когда оба числа оканчиваются на 0, вы можете разделить каждое на 10:
|
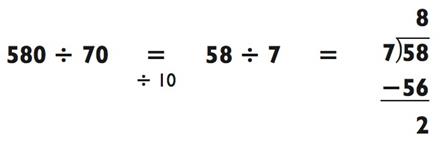
Если оба числа заканчиваются на 5, удвойте их, а затем разделите на 10 для упрощения задачи. Например:
|
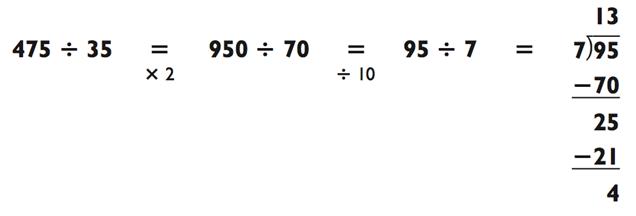
Наконец, если делитель оканчивается на 5, а делимое на 0, то умножьте оба на 2, а затем разделите на 10, прямо как мы делали выше:
|
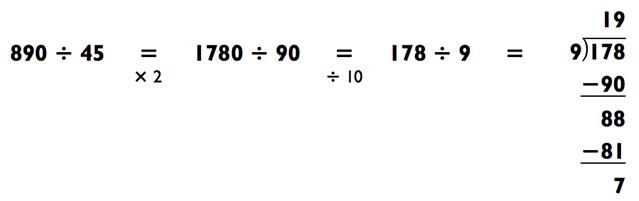
Дата: 2018-12-21, просмотров: 243.
