Вы можете использовать почти такие же техники, чтобы приблизительно оценивать свои ответы в задачах на умножение. Например,

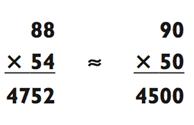
Округление до ближайшего кратного 10 значительно упрощает задачу, но ответ всё ещё отклоняется на 252, или около 5%. Вы можете улучшить ситуацию, если округлите оба числа на одинаковую величину, но в разных направлениях. То есть, если вы округлите 88 до 90, то вам так же следует уменьшить 54 на 2:

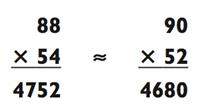
Вместо задачи типа «2-на-2» вы теперь имеете дело с умножением типа «2-на-1», что должно быть достаточно легко для вас. Ваша приближённая оценка отклоняется всего на 1,5%.

Когда ваш приближённый ответ для задачи на  умножение получен путём округления большего из чисел в большую сторону и меньшего - в меньшую, то ваш приближённый ответ будет немного занижен. Если вы округлите большее из чисел в меньшую сторону и меньшее - в большую (тогда числа станут достаточно близки), то ваш приближённый ответ будет слегка завышен. Чем больше величина, на которую вы округляете в ту или иную сторону, тем большее отклонение будет иметь ваша приближённая оценка. Например:

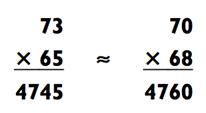
Так как числа стали близки к друг другу после вашего округления, приближённая оценка получилась немного завышенной.

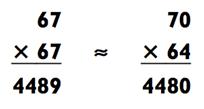
Так как числа находятся далеко друг от друга, приближённая оценка ответа занижена, однако, не намного. Вы можете заметить, что метод приближённой оценки работает весьма хорошо для примеров на умножение. Также обратите внимание на то, что данная задача есть

всего лишь 672  и что наша прикидка всего лишь первый шаг из техники возведения в квадрат. Давайте взглянем на ещё один пример:

Заметим, что аппроксимация является наиболее точной, когда исходные числа находятся близко друг к другу. Попробуйте прикинуть ответ для задачи типа «3-на-2»:

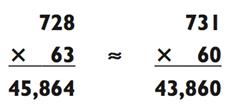
Путём округления 63 до 60 и 728 до 731 вы создаёте задачу типа

«3-на-1», что помещает вашу приближённую оценку в районе 2004 от точного ответа, ошибка размером 4,3%.

Теперь попробуйте дать приблизительную оценку следующей задачке «3-на-3»:

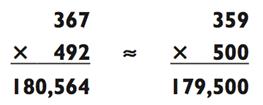
Вы заметите, что, хотя вы и округлили оба числа на 8 в разные стороны,  ваш  приближённый  ответ  будет  отклонятся  более  чем  на

1000. Это потому, что данная задача на умножение больше, и число, на которое вы округляете, больше. Так что получившаяся в результате оценка будет отклонятся на большую величину. Но относительная погрешность всё ещё будет меньше 1%.

Как далеко можно зайти с данной системой приближённой оценки для задачек на умножение? Как вам угодно. Просто  нужно знать названия больших чисел. Тысяча тысяч - миллион, тысяча миллионов - миллиард. Зная эти названия и числа, попробуйте задачку такого размера:

Как и ранее, задача состоит в округлении чисел, чтобы они стали простыми числами, такими как 29 000 000 и 14 000. Отбросив на

сейчас все 0, получим простую задачу «2-на-2»: 29 х 14 = 406 (29 х 14 =

29 х 7 х 2 = 203 х 2 = 406). Следовательно, ответ будет приблизительно

406 миллиардов, так как тысяча миллионов - это миллиард.