
Что за дверью номер 1?
Математическая банальность 1991 года, которая сделала всех вне себя от ярости, была статьёй Мэрилин Вос Савант (женщина, зарегистрированная Книгой Рекордов Гиннесса как человек с самым высоким в мире IQ) в журнале
«Parade». Данный парадокс стали известен как « проблема Монти Холла », и он выглядит следующим образом .
Вы участник « Давайте совершать сделки » (Let’s Make a Deal). Монти Холл даёт вам возможность выбрать одну из трёх дверей : за одной из этих дверей большой приз , за двумя другими - козы . Вы выбираете Дверь № 2. Но прежде чем Монти показывает приз , который вы выбрали , он показывает вам то , что вы не выбрали за Дверью № 3. Это коза . Теперь , в своей дразнящей манере , Монти предоставляет вам другой выбор : вы хотите продолжить с Дверью № 2 или вымхотите рискнуть шансом увидеть , что находится за дверью № 1? Что вам следует сделать ? Если предположить , что Монти собирается показать место , где отсутствует главный приз , то он все г да будет открывать одну из « утешительных дверей ». Это оставляет нас с двумя дверями : одна с большим призом , а другая с утешением . Сейчас шансы 50-50 для вашего выбора , не так ли ?
Неверно ! Шансы , что вы правильно выбрали в первый раз остаются 1 к 3. Вероятность того , что большой приз стоит за другой двери увеличивается до 2 к 3, потому что вероятности в сумме должны давать 1.
Таким образом , путем изменения дверей , вы удвоите шансы на выигрыш ! ( задача предполагает , что Монти всегда будет давать игроку возможность сделать это , что он всегда будет показывать « невыигрышную » дверь и что , когда ваш первый выбор является правильным , он будет выбирать
« невыигрышную » дверь наугад ) Поразмышляйте об игре с десятью дверями . И после вашего выбора он раскрывает восемь других « невыигрышных » дверей . Здесь ваши инстинкты , скорее всего , подскажут вам поменять дверь . Люди путают эту проблему с вариантами : если Монти Холл не знает , где главный приз , и раскрывает Дверь № 3, которая , как оказалось , содержит козу ( хотя это мог бы быть и приз ), то Дверь № 1 будет иметь 50- ти процентный шанс быть правильной . Данный результат настоль ко противоречит здравому смыслу , что Мэрилин Вос Савант получила груды писем ( многие от ученых и даже математиков ), в которых говорилось , что ей не следовало писать о математике . Все они были неправы .
Возведение в куб
Мы закончим эту главу новым методом для возведения в куб двузначных чисел. (Воскресите в памяти тот факт, что куб числа - это число, умноженное на себя дважды. Например, 5 в кубе - обозначаемое 53 — будет равно 5 х 5 х 5 = 125) Как вы убедитесь сами, это не намного труднее, чем умножение двузначных чисел. Метод основан на алгебраическом наблюдении, которое выявило, что
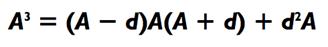
где d - любое число. Как и при возведении в квадрат двузначных чисел, я выбираю в качестве d так, чтобы оно было как можно ближе к кратному десяти. Например, когда возвожу в квадрат 13, то d = 3, а результате чего:
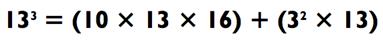
имеем
Так как 13 х 16 = 13 х 4 х 4 = 52 х 4 = 208, и 9 х 13 = 117, то мы
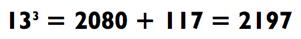
Как на счёт куба 35? Задавая d = 5, мы получаем
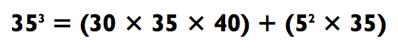
Так как 30 х 35 х 40 = 30 х 1400 = 42 000 и 35 х 5 х 5 = 175 х 5 =
875, мы получаем
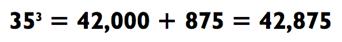
По ходу возведения 49 в куб, мы задаём d = 1 с целью округления до 50. Вот:
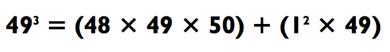
Мы можем решить 48 х 49 с использованием метода факторинга, но для задач такого типа я предпочитаю использовать метод
«совместной близости», который будет описан в Главе 8. (Можете забежать вперёд и взглянуть на него уже сейчас, если хотите!) Используя этот метод, мы получаем 48 х 49 = (50 х 47) + (1 х 2) = 2352. Умножив это число на 50, мы получаем 117 600 и вследствие этого
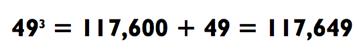
А вот задачка покрупнее. Попробуйте возвести в куб 92.
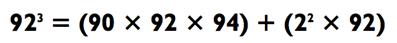
Если вы можете быстро возводить в квадрат двузначные числа, значит вы сможете решить 92 х 94 = 932 - 1 = 8648, или вы могли бы использовать метод «совмесной близости», следствие которого 92 х 94
= (90 х 96) + (2 х 4) = 8648. Умножив это число на 9 (как описано в
начале Главы 8), мы получим 9 х (8600 + 48) = 77 400 + 432 = 77 832, и,
следовательно, 90 х 92 х 94 = 778 320. Так как 4 х 92 = 368, то мы получаем
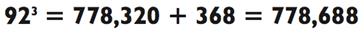
Отметим, что при использовании метода «совместной близости» для задач на умножение, возникающих при возведении в куб трёхзначного числа, малое произведение, которое нужно прибавить (в
зависимоти от того, равняется ли d = 1, 2, 3, 4, или 5), будет 1 х 2 = 2, 2
х 4 = 8, 3 х 6 = 18, 4 х 8 = 32 либо 5 х 10 = 50. Давайте закончим с кубом
96.
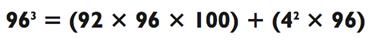
Произведение 92 х 96 = 8832 может быть посчитано множеством разных способов. Дабы отпраздновать окончание данной Главы, давайте используем некоторые из них. Я начну с самого сложного, на мой взгляд, а закончу наилегчайшим. По результатам метода сложения (90 + 2) х 96 = 8640 + 192 = 8832; по результатам метода вычитания 92 х
(100 - 4) = 9200 - 368 = 8832; по результатам метода факторинга 92 х 6 х
4 х 4 = 552 х 4 х 4 = 2208 х 4 = 8832; по результатам возведения в
квадрат 942 - 22 = 8836 - 4 = 8832; по результатам метода совмесной
близости с основой в виде 90, (90 х 98) + (2 х 6) = 8820 + 12 = 8832; и по результатам метода совмесной близости с основой в виде 100, (100 х 88) + (-8 х -4) = 8800 + 32 = 8832.
Произведение 42 х 96 = 1536 может быть так же посчитано несколькими способами, такими как 96 х 4 х 4 = 384 х 4 = 1536 или 16 х (100 -
4) = 1600 - 64 = 1536. И наконец, так как 8832 х 100 = 883 200, мы имеем
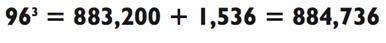
Дата: 2018-12-21, просмотров: 432.