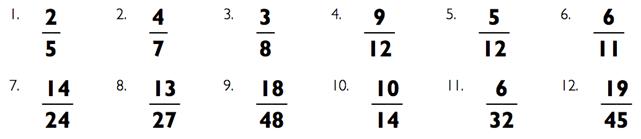
Чтобы решить следующие задачи, не забудьте использовать полученные знания о десятичном виде различных «одноцифровых» дробей. Везде, где это целесообразно, упрощайте дроби, прежде чем преобразовать их в десятичные.

Тестирование на делимость

В последнем разделе мы увидели, как задачки на деление могут быть упрощены, если оба числа поделить на общий множитель. Мы закончим эту главу кратким обсуждением того, как  определить, является ли одно число множитилем другого. Возможность определить множитель числа помогает нам упростить задачу на деление и может ускорить процесс решение многих задач на умножение. Это также будет очень полезным инструментом, когда мы доберёмся до продвинутого умножения, где вы частенько будете искать способы разложить на множители двух-, трех-, или даже пятизначный числа посреди решения задачки на умножение. Способность быстро разлагать эти числа будет весьма полезна. И кроме того, я думаю, что некоторые из правил просто сами по себе прекрасны.

Легко проверить, делится ли число на 2. Всё, что вам нужно сделать, это проверить, является ли последняя цифра чётной. Если последняя цифра 2, 4, 6, 8, или 0, то и число целиком делится на 2.

Чтобы протестировать число на способность делится на 4, проверьте, делится ли последняя цифра двузначного числа на 4. Число 57 852 кратно 4, потому что 52 = 13 х 4. Число 69 346 не кратно 4, поскольку 46 не кратно 4. Причина, по которой это работает, состоит в том, что 4 делит равномерно делит 100 и, следовательно, в любое кратное 100 число. Отсюда, так как 4 равномерно делит в 57 800, и 52

делится на 4, мы знаем, что 4 равномерно поделит их сумму, 57 852.

По такому же принципу, так как 1000 делится на 8, для теста на делимость 8, проверьте последние три цифры числа. Число 14 918 делится на 8 как 918. Но раз уж такое действие завещает нам остаток (918 ÷ 8 = 114 6/8), то это число не делится на 8. Вы также могли наблюдать это, если заметили, что 18 (последние две цифры 14 918) не

делится на 4, а так как 14 918 не делится на 4, оно не может делиться и на 8.

Когда дело доходит до делимости на 3, предлагаю вам воспользоваться классным правилом, которое легко запомнить: число делится на 3 тогда, и только тогда, когда сумма  составляющих  его цифр делятся на 3 (независимо от того, сколько цифр в числе). Для проверки того, делится ли 57 852 на 3, просто сложите 5 + 7 + 8 + 5 + 2

= 27. Так как 27 кратно 3, то мы теперь знаем, что 57 852 кратно 3. Такое же удивительное правило справедливо для делимости на 9. Число делится на 9 тогда, и только тогда, когда сумма составляющих его цифр кратна 9. Следовательно, 57 852 кратно 9 , тогда как число 31 416, которое в сумме даёт 15, вовсе нет. Причина, по которой это работает, основана на том, что числа 1, 10, 100, 1000, 10000, и так далее, всегда на единицу больше, чем кратное 9.

Число делится на 6 тогда, и только тогда, когда оно чётное и делится на 3. Так что легко провести тест на делимость на 6.

Установить, делится ли число на 5, ещё проще. Любое число, независимо от своей величины, кратно 5 тогда, и только тогда, когда оно оканчивается на 5 или 0.

Установление делимости на 11 почти такое же простое, как определение делимости на 3 или 9. Число делится на 11 тогда,  и только тогда, когда вы придёте либо в 0, либо к кратному 11 в результате попеременного вычитания и сложения  составляющих число цифр. Например, 73 958 не делится на 11 , так как 7 - 3 + 9 - 5 + 8

= 16. Однако числа 8492 и 73 194 кратны 11, так как 8 - 4 + 9 - 2 = 11 и 7

- 3 + 1 - 9 + 4 = 0. Причина, по которой это работает, основана, как и правило для 3 и 9, на том, что числа 1, 100, 10 000, 1 000 000 на

единицу больше, чем один кратное 11, в то время как числа 10, 1000, 100 000, и так далее на единицу меньше величины, кратной 11.

Тестирование делимости на 7 немного сложнее. Если вы прибавляете (вычитаете) число, которое кратно 7, к (из) числу(а), которое вы тестируете, и полученное число делится на 7, то результат теста положительный. Я всегда выбираю, чтобы прибавляемое или вычитаемое кратное 7, было таким, что в результате сумма или разность заканчивалась бы на 0. Например, для проверки числа 5292, я вычитаю 42 (кратное 7), чтобы получить 5250. Далее, я избавляюсь от 0 на конце (так как деление на десять не влияет проверку делимости на семь), получая в итоге 525. Затем я повторяю процесс, прибавляя 35 (кратное 7), что дает мне 560. Когда я удаляю 0, то остаюсь с числом 56, которое, как мне известно, кратно 7. Таким  образом,  исходное число 5292 является делимым на 7.

Этот метод работает не только для 7, но и для любого нечетного числа, которое не оканчивается на 5. Например, чтобы проверить, делится ли 8792 на 13, вычитаем 4 х 13 = 52 из 8792 для получения

8740. Опуская 0, имеем следствием 874. Затем прибавляем 2 х 13 = 26, чтобы получить 900. Удаление двух 0 оставляет вас с числом 9, которое, очевидно, не кратно 13. Таким образом, 8792 не кратно 13.