Теперь, когда вы умеете решать задачи типа «2-на-1» в уме, умножение трёхзначных чисел на состоящие из одной цифры не покажется вам более сложным. Вы можете начать со следующего примера типа «3-на-1» (который на самом деле представляет собой замаскированный «2-на-1»):

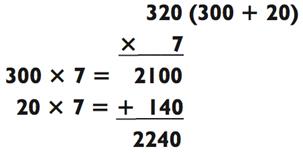
Было ли это легко? (если данный пример доставил трудностей, вам должно быть следует пересмотреть материал по сложению в Главе

1) Давайте попробуем решить ещё один пример «3-на-1», подобный тому, который вы только что посчитали, но уже заменим 0 на 6, чтобы у вас появилось ещё одно действие для выполнения:

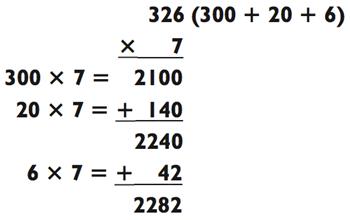
В  данном  случае,  вы  просто  прибавляете  результат  от  6  х  7,

который уже известен как 42, к первой сумме 2240. Так как вам не

нужно запоминать никакие числа, то будет легко сложить 42 с 2240 и получить в итоге 2282.

При решении данной и других задач типа «3-на-1» камнем преткновения может стать удержание в памяти первой суммы (в этом примере - 2240), в то время как вы заняты умножением (здесь - 6 х 7). Не существует какого-либо магического секрета для запоминания первого числа, но я гарантирую, что с практикой вы улучшите свою концентрацию, и удержание чисел в памяти параллельно с другими операциями станет легче.

Давайте решим ещё одну задачу:

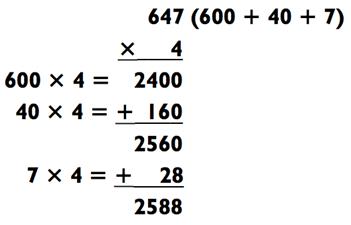
Даже если числа большие, сам процесс прост. Например:

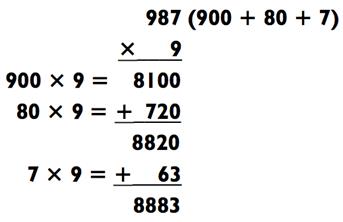
Когда вы впервые решаете такие задачки, то должно быть поглядываете на записи, дабы напомнить себе, какое было изначальное условие. По-началу это нормально. Но попытайтесь избавиться от данной привычки, чтобы со временем научиться удерживать задачу целиком в памяти.

В прошлом разделе об умножении типа «2-на-1» мы увидели, что примеры, включающие в себя числа с пятёркой на конце, особенно лёгкие в решении. Это же верно и для задач типа «3-на-1»:

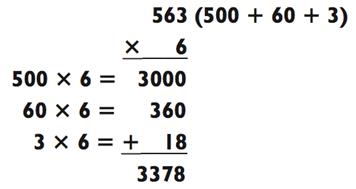
Обратите внимание, что всякий раз, когда первый результат умножения получается кратным 1000, следующая проблема сложения уже вовсе не проблема. Это потому, что вам не нужно запоминать никакие числа и порядковый номер тысячи не меняется. Если бы вы решали эту задачу (см. выше) перед кем-то, то могли бы сказать вслух

«три тысячи…» с абсолютной уверенностью в том, что число в уме не превратит ответ в 4000. (В качестве дополнительного бонуса, называя первые цифры, вы создаёте иллюзию, будто мгновенно вычислили ответ!) Но даже если вы тренируетесь в одиночестве, проговаривание первых результатов вслух освобождает часть оперативной памяти, пока вы продолжаете работу над оставшимися действиями задачи типа «2-на-1», результаты решения котороый вы так же можете произнести вслух, например, «…триста семьдесят восемь.»

Попробуйте такой подход при решении  следующей  проблемы, где множителем выступает 5:

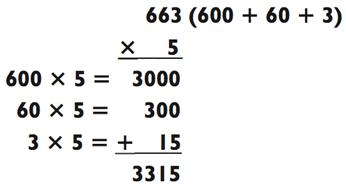
Так как первые две цифры трёхзначного числа одинаковые, вы можете произносить ответ паралелльно с вычислениями даже без необходимости складывать что-либо! Разве вам не хотелось бы, чтобы все задачки на умножение были такими лёгкими?

Давайте поднимемся на новый уровень сложности и попробуем решить пару примеров, которые требуют от нас держать в уме числа.

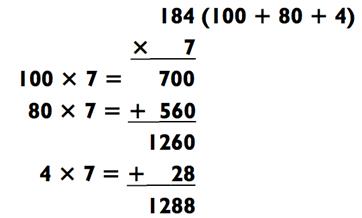
В следующих двух примерах вам нужно держать числа в уме на последнем этапе решения, а не в его начале:

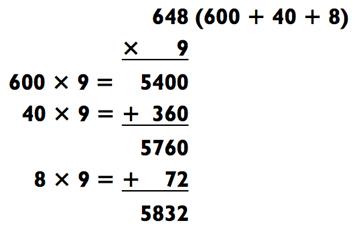
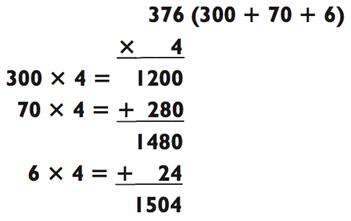
Первое действие для каждой задачи легко произвести в уме. Сложности наступают, когда необходимо удержать в памяти предварительный ответ, параллельно вычисляя итоговый. В случае с первой задачей, легко сложить 5400 + 360 = 5760. Но вы будете вынуждены повторять «5760» самому себе несколько раз, пока умножаете 8 х 9 = 72. Затем складываем 5760 + 72. Иногда, на этой стадии, я начинаю проговаривать ответы вслух ещё до завершения. Так как я знаю, что нужно будет держать числа в уме, когда я буду складывать 60 + 72, то я также знаю, что 5700 станет 5800. Я говорю:

«пятьдесят восем сотен (пять тысяч восемь сот)…» Затем я приостанавливаюсь для сложения 60 = 72 = 132. Потому что я уже держу  числа  в  уме,  я  произношу  только  последние  две  цифры:

«… тридцать два!» А вот и ответ: 5832.

Обе следующие задачи требуют от вас держать два числа в уме, так что их решение может занять больше времени, чем ранее. Но с практикой вы станете быстрее:

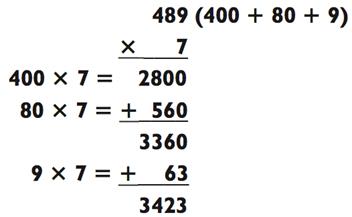
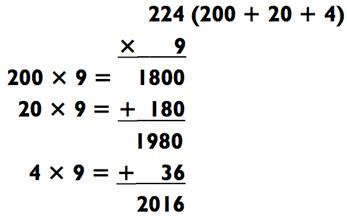
Когда вы впервые принимаетесь за решение таких примеров, повторяйте ответ для каждого действия вслух, параллельно вычисляя остальное. В первой задаче, например, начните с: «Двести восемьдесят (двадцать восем сотен) плюс пятьсот шестьдесят (пять сотен шестьдесят)», проговорив пару раз всё это вслух, тем самым закрепив два числа в памяти, пока складываете их. Повторите ответ -

«три тысячи триста тридцать (тридцать три сотни шестьдесят)» - несколько раз, пока умножаете 9 х 7 = 63. После повторяйте «три тысячи триста тридцать (тридцать три сотни шестьдесят) плюс шестьдесят три» вслух до тех пор, пока не вычислите итоговый ответ 3423. Если вы достаточно быстро соображаете, чтобы распознать то, что сложение 60 + 63 потребует от вас удержать в уме 1, тогда вы в состоянии озвучить итоговый ответ на долю секунды быстрее,  чем сами это осознаете - «три тысячи четыреста (тридцать четыре сотни) и… двадцать три!»

Давайте завершим раздел с задачами на умножение типа «3- на-1» рядом особых примеров, которые вы можете мгновенно решить, так как они требуют лишь одного действия на сложение, вместо двух:

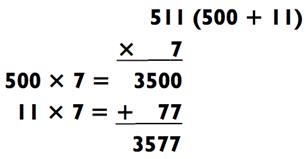
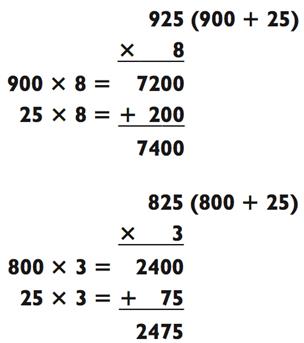
В общем случае, если результат умножения последних двух цифр первого числа на его множитель известен вам и без подсчётов (например, вы можете знать, что 25 х 8 = 200, так как 8 четвертаков равны $2,00), то вы сможете получить итоговый ответ намного быстрее. Например, если вам без расчётов известно, что 75 х 4 = 300, то легко будет посчитать 975 х 4:

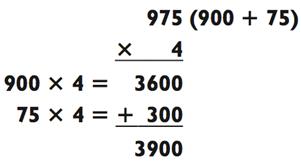
Чтобы закрепить только что пройденное, решите следующие задачки на умножение типа «3-на-1» в уме; затем проверьте свои вычисления и ответы, используя наши (в конце книги). Я могу вас уверить из собственного опыта в том, что устные вычисления сродни катанию на велосипеде или печатанию. Это может казаться невозможным по-началу, но как только вы всё освоите, то уже никогда не забудете как это делается.