

Возведение в квадрат двузначных чисел
Возводить числа в квадрат в уме (умножать число само на себя) одно из наиболее лёгких, но в то же время, и одно из наиболее впечатляющих ловкачеств из арсенала устных вычислений. Я до сих пор помню, где я находился, когда открыл для себя это. Мне было тринадцать. Я сидел в автобусе, который вёз меня навестить отца на работе в центр Кливленда. Это была привычная поезка для меня,
поэтому мысли начали блуждать. Я не помню почему, но я начал думать о числах, которые в сумме дают 20. И я задумался о том, каким большим может быть результат действий с этими числами?
Я начал с середины, 10 х 10 (или 102 ), результатом чего является
100. Затем, я умножил 9 х 11 = 99, 8 х 12 = 96, 7 х 13 = 91, 6 х 14 = 84,
5 х 15 = 75, 4 х 16 = 64, и так далее. Я обратил внимание на то, что результат каждый раз уменьшается. И разница между ним и 100 была 1,4,9,16,25,36, . . . или 12, 22, 32, 42, 52, 62, . . . (смотри таблицу ниже)
Числа, дающие в сумме 20
Мне данный паттерн представился удивительным. Затем я опробовал числа, дающие в сумме 26, и результаты были похожими. Первым делом я прорешал примеры 132 = 169, затем 12 х 14 = 168, 11 х
15 = 165, 10 х 16 = 160, 9 х 17 = 153, и так далее. Как и прежде,
расстояния этих произведений от 169 равнялись 12, 22, 32, 42, и так далее (смотри таблицу ниже).
На самом деле, существует простое алгебраичиское объяснение данного феномена (смотри «Почему эти приёмы работают»). Но в то время, я не разбирался в алгебре достаточно хорошо, чтобы доказать
постоянство появления данного паттерна, но я провёл достаточное количество экспериментов с подобными примерами, чтобы убедиться в его существовании.
Затем я осознал, что данный шаблон может помочь мне сделать возведение чисел в квадрат намного легче. Предположим, я хотел возвести в квадрат 13. Вместо того, чтобы умножать 13 х 13,
|
Числа, дающие в сумме 26 | Расстояние от 13 | Их произведение | Расстояние их произведения от 169 | |
| 13 | 13 | 0 | 169 | 0 |
| 12 | 14 | 1 | 168 | 1 |
| 11 | 15 | 2 | 165 | 4 |
| 10 | 16 | 3 | 160 | 9 |
| 9 | 17 | 4 | 153 | 16 |
| 8 | 18 | 5 | 144 | 25 |
почему бы не получить приближённый ответ, используя два числа, которые легче перемножить, но которые также дают в сумме 26? Я выбрал 10 х 16 = 160. Чтобы получить итоговый ответ, я просто прибавил 32 = 9 (так как 10 и 16 находятся на расстоянии 3 от 13).
Таким образом, 132 = 160 + 9 = 169. Всё чётко!
Данный метод схематически можно представить так:
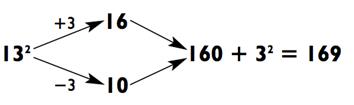
А теперь давайте посмотрим, как это работает с квадратом другого числа:
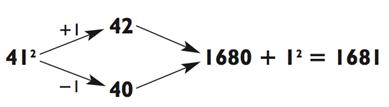
Чтобы возвести в квадрат 41, вычтем 1 для получения 40 и добавим 2 для получения 42. Далее умножаем 40 х 42. Без паники! Это простое умножение типа «2-на-1» под прикрытием (4 х 42, в частности). Так как 4 х 42 = 168, 40 х 42 = 1680. Почти всё! Вам необходимо лишь прибавить квадрат 1 (числа, на величину которого вы уменьшали и увеличивали 41), чтобы получить 1680 + 1 = 1681.
Способно ли возведение в квадрат двузначных чисел быть таким лёгким? Да, с использованием этого метода и небольшим количеством практики, может. И это работает в независимости от того, округляете ли вы исходное число в большую или меньшую сторону.
Например, давайте проверим 772, округлив его во время решения в обе стороны:
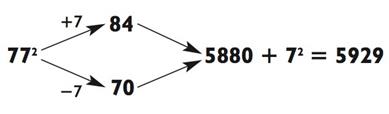
ИЛИ
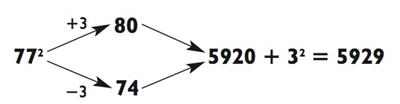
В данном примере преимущество округления в большую сторону состоит в том, что вы практически уже получили решение, осталось лишь просто прибавить 9 к числу с 0 на конце!
По сути, я всегда округляю по принципу большей близости к 10. Так, если возводимое в квадрат число оканчивается на 6, 7, 8, или 9, то округление в большую сторону. И если возводимое в квадрат число оканчивается на 1, 2, 3, или 4, то округление в меньшую сторону. (если число оканчивается на 5, то сразу оба!) Придерживаясь данной стратегии, вы ограничитесь лишь прибавлением чисел 1, 4, 9, 16 или 25 к результатам первой калькуляции.
Давайте рассмотрим другой пример. Вычислите 562 в уме самостоятельно, прежде чем смотреть на наше решение ниже:
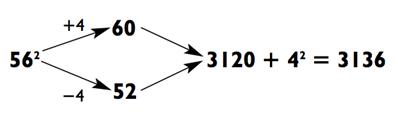
Возведение в квадрат чисел, оканчивающихся на 5 ещё легче. Так как вы каждый раз будете округлять в любую из сторон на величину 5; числа, которые нужно будет перемножить, будут кратны
10. Следовательно, умножение и сложение покажутся особенно простыми. Ниже представлены решения для 852 и 352:
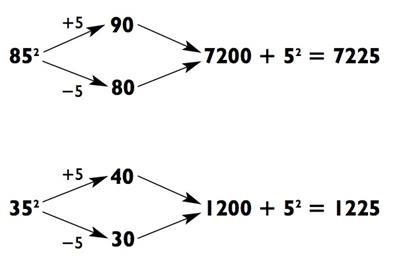
Как вы можете знать из Главы 0, когда происходит возведение в квадрат чисел, оканчивающихся на 5, округление в большую и меньшую стороны позволяет вам немедленно «выпаливать» первую часть ответа, а потом заканчивать его числом 25. Например, когда вы хотите посчитать 752, округление до 80 и 70 даст вам: «пятьсот шестьдесят (пятьдесят шесть сотен) и… двадцать пять!»
Что касается чисел, оканчивающихся на 5, у вас не должно возникнуть проблем с разгромом кого-либо с калькулятором в руке. А после небольшого количества практики с другими примерами на возведение в квадрат, момент, когда вы сможете победить калькулятор в борьбе по возведению в квадрат, не заставит себя долго ждать. Вы даже не испугаетесь больших чисел. Вы можете попросить кого-нибудь загадать вам действительно большое двузначное число, что-нибудь на подобие 90>, и это будет выглядеть, будто вы взяли на себя непосильную задачу.
Но на самом деле это ещё легче, потому что у вас будет возможность округлить до 100.
Давайте представим, что ваша аудитория задала вам 962.
Сначала попробуйте сами, а уже потом смотрите на наше решение:
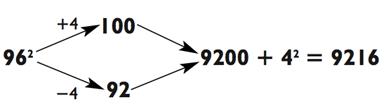
Не было ли это легко? Вам следовало округлить с помощью 4 до 100 и округлить с помощью 4 до 92, а затем умножить 100 х 92 для получения 9200. В этот момент вы можете проговорить вслух: «Девять
тысяч двести (девяносто две сотни)…» и после закончив, используя
«шестнадцать». И наслаждаться аплодисментами.
Дата: 2018-12-21, просмотров: 590.