Этот раздел представлен для учителей, студентов, любителей математики и всех любопытствующих по поводу того, почему этот метод работает. Некоторые из вас найдут теоретическую сторону вопроса не менее интересной, чем практическую. К счастью, вам не нужно разбираться в том, почему данный метод работает, чтобы разобраться в том, как его применять. За всеми магическими трюками скрывается рациональное объяснение. И математические трюки не исключение. И вот, прямо сейчас, матемаг раскрывает свои самые сокровенные тайны!
В этой главе, посвящённой задачкам на умножение, это был распределительный закон, который позволял нам разбивать примеры на части. Данный закон гласит, что для любых чисел a, b и c:
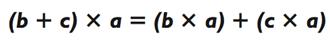
То есть, число за скобками распределяется, или по отдельности применяется, к каждому из чисел в скобках, b и c. Например, в нашей первой задачке на умножение 42 х 7 мы добрались до итогового ответа с помощью представления 42 в виде 40 + 2, а затем распределили 7 следующим образом:
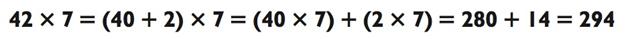
Вы можете задаться вопросом «Почему распределительный закон в принципе работает?» Для интуитивного осознания этого, представьте, что у вас 7 сумок, в каждой по 42 монеты, 40 из которых золотые и 2 серебряные. Сколько всего у вас монет? Существует 2 способа получить ответ. Сперва, исходя из самого определения
умножения, у вас 42 х 7 монет. С другой стороны, всего 40 х 7 золотых и 2 х 7 серебряных монет. Следовательно, мы имеем (40 х 7) + (2 х 7) монет вместе. Отвечая на наш вопрос двумя способами, получим 42 х 7
= (40 х 7) + (2 х 7). Обратите внимание, что числа 7, 40, и 2 могут быть заменены любым другим (a, b или c) с сохранением общего логического принципа. Вот почему распределительный метод работает!
Используя схожую аргументацию про золотые, серебряные и медные монеты, мы получаем:
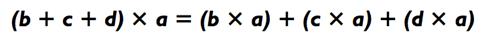
Следовательно, чтобы решить пример 326 х 7, мы разбиваем 326
как 300 + 20 + 6. Затем распределяем 7 следующим образом: 326 х 7 =
(300 + 20 + 6) х 7 = (300 х 7) + (20 х 7) + (6 х 7), а потом складываем полученное для получения ответа.
Что касается возведения в квадрат, ниже представленный алгебраический закон оправдывает мой метод. (A и d - любые числа)
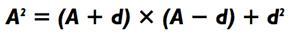
Здесь, А - число, которое возводится в квадрат; d - любое число, но я выбрал в качестве такого числа отдалённое от А на величину ближайшего кратного 10. Поэтому для 772 я установил d = 3, и наша формула подсказывает, что 772 = (77 + 3) х (77 - 3) + 32 = (80 х 74) + 9
= 5929. Алгебраические отношения следующего вида также объясняют мой метод возведения в квадрат:
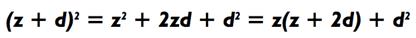
Следовательно, чтобы возвести в квадрат 41, мы зададим z = 40
и d = 1, чтобы получить:
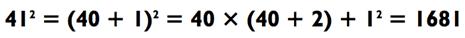
Схожим образом,
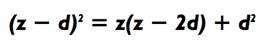
чтобы найти 772 w когда z = 80 и d = 3,
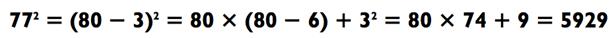
|
Дата: 2018-12-21, просмотров: 380.
