Матемагия действительно становится захватывающей, когда вы выступаете перед аудиторией. Мой первый опыт публичных выступлений пришёлся на восьмой класс, в довольно «преклонном возрасте» тринадцати лет. Многие матемаги начинали ещё раньше. Зера Колберн (1804-1839), например, как сообщается, мог производить молниеносные расчёты, ещё до того, как научился читать и писать, и он уже развлекал зрителей в возрасте шести лет! Когда мне было тринадцать, мой учитель алгебры записал на доске задачку, ответом для которой было 1082. Не намереваясь на этом останавливаться, я выпалил: «Квадрат 108 всего лишь 11 664!»

Учитель сделал расчет на доске и получил такой же ответ. Глядя немного напуганно, она произнесла: «Да, верно. Как ты это сделал?» Ну я ей и рассказал: «Я округлил 108 до 100 и увеличил 108 до 116. После я перемножил 116 х 100, получил 11 600, а потом просто

прибавил квадрат 8, чтобы получить 11 664.»

Она никогда раньше не сталкивалась с таким методом. Я был взволнован. Мысли о «Теореме Бенджамина» приходили мне в голову. Я на самом деле верил в то, что открыл нечто новое. Когда я в конце концов наткнулся на данный метод спустя несколько лет в книге Мартина Гарднера по рекреационной математике «Математический крнавал» (1965), мой день был испорчен! Хотя тот факт, что я сам пришёл к этому, был очень воодушевляющим.

Вы тоже можете произвести впечатление на своих друзей (или учителей), используя некоторые из довольно удивительных расчётов на умножение. В конце прошлой Главы вы узнали, как умножить двузначное  число  само  на  себя.  В  этой  главе  вы  узнаете,  как

перемножить два разных двузначных числа - сложное, но ещё более творческое задание. Затем вы попробуете приложить свою руку (или, точнее, ваш мозг) к возведению трёхзначных чисел в квадрат. Вам нет необходимости знать, как решать задачи на умножение двух двузначных чисел, чтобы решать задачи по возведению в квадрат трёхзначных, так что вы можете начать изучение с любого из навыков.

Задачи на умножение типа «2-на-2»

Когда вы возводите в квадрат двузначное число, метод всегда одинаковый. Однако, когда вы перемножаете двузначные числа, то вы можете использовать множество разных методов, которые  приведут вас к одному и тому же ответу. Лично для меня, здесь и начинается самое весёлое.

Метод сложения

Чтобы использовать метод сложения для перемножения двух двузначных чисел, вам всего лишь необходимо решить две задачки на умножение типа «2-на-1» и сложить результаты. Например:

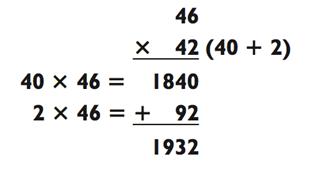
Здесь вы разбиваете 42 на 40 и 2: два числа, на которые легко потом умножать. После вы умножаете 40 х 46, а это всего лишь 4 х 46 с добавочным 0, или 1840. Затем вы умножаете 2 х 46 = 92. Наконец, вы складываете 1840 + 92 = 1932, как и показано выше.

Вот ещё один способ решения той же задачи:

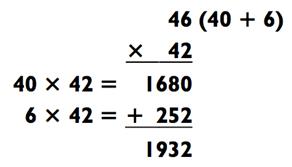
Подвох в том, что умножить 6 х 42 сложнее, чем умножить 2 х 46, как в первой задаче. Более того, прибавить 1680 + 252 сложнее, чем 1840 + 92. Так как определиться с тем, какое из чисел  разбить  на части? Я стараюсь выбирать число, действия над которым приведут к более простой задаче на сложение. В большинстве случаев, но не всегда, вам будет хотеться разбить число с наименьшей цифрой на конце, потому что это обычно выливается в меньшее число для сложения в будущем.

А сейчас попробуйте свои силы на следующих примерах:

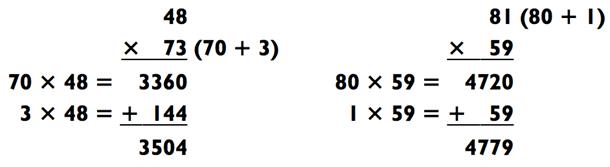
В последнем примере проиллюстрировано то, почему числа с 1 на конце так привлекательны для разбиения. Если оба числа оканчиваются на одинаковую цифру, вам следует делить на части более крупное число, как показано ниже:

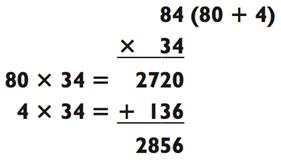
Если одно из чисел на много больше другого, то его разбиение часто оправдывает себя, даже если цифра на конце больше. Вы поймёте, что я имею в виду, когда прорешаете следующие задачи двумя разными способами:

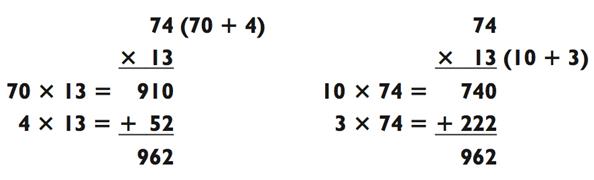
Показался ли вам первый способ быстрее второго? Мне показался. Вот ещё одно исключение из правила «разбивайте на части число с наименьшей цифрой на конце». Когда вы будете умножать число типа 50> на чётное число, вам захочется разбить на части именно число типа 50>:

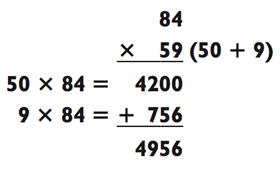
Цифра на конце у числа 84 меньше, чем у числа 59. Но если вы разделите на части 59, результаты умножения будут кратны 100, прямо как 4200 из примера выше. Это делает последующие задачи на сложение многим легче.

А теперь опробуйте лёгкую задачку другого типа:

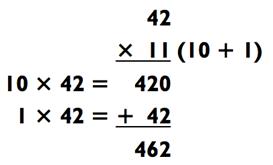
Хотя вычисления, показанные выше, достаточно простые, существует ещё более лёгкий и быстрый способ умножения числа на

11. Это матемагия во всей своей красе: вы не поверите своим глазам, когда увидите это! (если вы, конечно, ещё не забыли про Главу 0)

Вот как это работает. Представьте себе двузначное число, цифры которого в сумме дают 9 или меньше. Для умножения такого числа на 11, просто сложите эти две цифры и вставьте полученную сумму между двух исходных цифр. Например, чтобы умножить 42 х 11, сначала сложите 4 + 2 = 6. Если вы поместите 6 между 4 и 2, то получите 462, что и является решением!

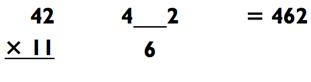
Решите 54 х 11, используя данный метод.

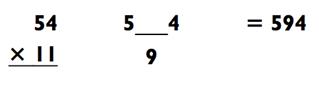
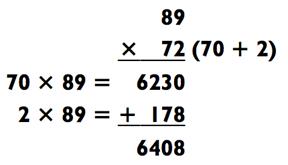
Если вы получили правильный ответ с первого или второго раза, похлопайте себя по спине. В действительности, не найдётся задач на умножение типа «2-на-2» труднее этой. Если вы не получили ответ сразу, не волнуйтесь. В следующих двух разделах я обучу вас гораздо более лёгким стратегиям для решения подобных  задач.  Но  прежде, чем вы продолжите чтение, попрактикуйте метод сложения на следующих задачах на умножение.