Вундеркинд - это очень талантливый ребёнок, обычно называемый «не по годам развитым» или «одаренным», почти всегда опережающий своих сверстников. Немецкий математик Карл Фридрих Гаусс (1777-1855) был одним из таких детей. Он часто хвастался тем, что научился производить расчёты раньше, чем говорить. В зрелом возрасте трех лет, прежде чем его начали учить какой-либо арифметике, он подправил платёжную ведомость отца, заявив: «Подсчёты неверны». Дальнейшая проверка чисел показала, что молодой Карл был прав.

В качестве десятилетнего ученика , Га усс п о лу чи л сл е д у ющ у ю математическую задачу : какова сумма чисел от 1 до 100? В то время , как его сокурсники отчаянно производили расчеты с бумагой и карандашом , Гаусс сразу представил себе , что если он рассредоточит цифры от 1 до 50 слева направо , а числа с 51 по 100 справа налево прямо под списком цифр 1-50, то каждая комбинация в сумме будет давать 101 (1 + 100,2 + 99,3 + 98, ...). Так как там всего пятьдесят сумм , ответ будет 101 х 50 = 5050. Ко всеобщему изумлению ( включая у чителя ), юный К арл пол у чил ответ не только опередив всех остальных , но и вычислив его целиком в уме . Он записал ответ на своей грифильной доске и швырнул его на стол учителя с дерзким : « Вот он лежит ». Учитель был настолько впечатлен , что он инвестировал свои собственные деньги , чтобы купить наилучший из доступных учебников по арифметике и отдал его Гауссу , заявив : « Он находится за пределами моих возможностей , я больше ничему не смогу его научить ».

Действительно , Гаусс стал учителем математики для других , и в конечном итоге продвинулся дальше , чтобы стать одним из величайших математиков в истории , чьи теории до сих пор на службе науки . Желание Гаусса лучше понимать природу через язык математики было подытожено в его девизом , взятом из шекспировского Короля Лира ( заменяя « закон » на « законы »): « Природа , ты моя богиня ! В жизни Я лишь твои законам послушен »

Упражнение: сложение трёхзначных чисел

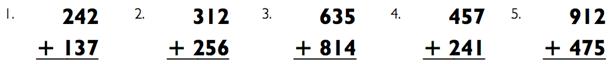
Вычитание слева направо

Для большинства из нас, сложение легче вычитания. Но если вы продолжите вычитать слева направо и разбивать примеры на более простые действия, вычитание может стать  почти  таким  же  простым, как  сложение.

Вычитание двузначных чисел

В процессе вычитания двузначных чисел вы преследуете цель упростить задачу, доведя её до вычитания (или сложения) однозначного числа. Давайте начнём с очень простого примера на вычитание:

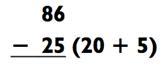
После каждого действия вы прибываете на новый и более лёгкий этап вычитания. Здесь мы сперва отнимаем 20 (86 - 20 = 66),

далее мы отнимаем 5, чтобы достигнуть самого простого действия 66 -

5 для получения итогового ответа 61. Задача может быть схематически представлена как: