Карлсон предложил Малышу сыграть в такую игру. На столе лежит кучка спичек. Карлсон и Малыш по очереди берут несколько спичек. Брать можно одновременно не более 5 спичек. Первым берёт Карлсон. Выигрывает тот, кто возьмёт последнюю спичку. Давай научимся хорошо играть в эту игру.
Понятно, что если на столе спичек 5 или меньше, то Карлсон выиграл. Он сразу возьмёт все спички. До Малыша даже ход не дойдёт. А что будет, если на столе 6 спичек? В этом случае Карлсон проигрывает. Сколько бы он ни взял, Малыш забирает остальные. Убедись в этом! Ведь хотя бы одну спичку Карлсон должен взять! А все взять не может!
Пусть теперь на столе лежит 7 спичек. Сколько спичек должен взять Карлсон, чтобы наверняка выиграть? (Карлсон должен взять одну спичку.)
– Заполните таблицу.
В колонке «Кто выигрывает» ставьте букву М (Малыш) или К (Карлсон), а в колонке «Первый ход» впишите, сколько спичек должен взять Карлсон, начиная игру, чтобы выиграть (если это возможно).
| Число спичек | Кто выигрывает | Первый ход |
| 6 | М | – |
| 7 | К | 1 спичка |
| 8 | К | 2 спички |
| 9 | К | 3 спички |
| 10 | К | 4 спички |
| 11 | К | 5 спичек |
| 12 | М | – |
| 13 | К | 1 спичка |
| 14 | К | 2 спички |
| 15 | К | 3 спички |
| 16 | К | 4 спички |
| 17 | К | 5 спичек |
– В каких случаях Малыш может выиграть, как бы ни старался Карлсон? (Если на столе лежит 6 спичек, 12 спичек, 18 спичек.)
– Во всех других случаях Карлсон может выиграть.
– Какой первый ход должен сделать Карлсон, если на столе лежит:
а) 15 спичек? Первым ходом надо взять 3 спички.
б) 23 спички? Первым ходом надо взять 5 спичек.
в) 32 спички? Первым ходом надо взять 2 спички.
– С точки зрения Карлсона, числа делятся на «хорошие» и «плохие». Плохими являются числа, которые делятся на 6. А «хорошие» – не делятся на 6.
Если число «хорошее», то своим ходом Карлсон берёт столько спичек, сколько надо, чтобы осталось «плохое» число.
– А какие числа будут «плохими», если можно брать:
а) не более 4 спичек? «Плохие» числа – это числа, которые делятся на 5;
б) не более 6 спичек? «Плохие» числа – это числа, которые делятся на 7;
в) не более 7 спичек? «Плохие» числа – это числа, которые делятся на 8.
IV. Итог урока.
– Для каких действий выполняется сочетательный закон?
Урок 130
Решение задач с помощью
составления выражений
Цель деятельности учителя: способствовать формированию умения решать текстовые задачи с помощью составления выражения и используя шифр.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: адекватно ведут себя в процессе учебной деятельности; выражают положительное отношение к процессу познания.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: определяют при сопоставлении с образцом учителя или показом в учебнике верно выполненное задание от неверного; высказывают свое предположение на основе работы с учебником; познавательные: приводят примеры в качестве доказательства выдвигаемых положений; выполняют учебные задачи, не имеющие однозначного решения; коммуникативные: описывают объект, передавая его внешние характеристики; слушают и понимают речь других (одноклассников, учителя).
Ход урока
I. Устный счет.
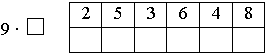
| 1. Отгадайте загадку и выполните умножение. В лес со мною соберешься, И с пути ты не собьешься.
| 
| ||
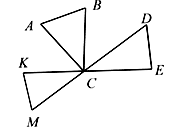
| 2. Рассмотрите рисунок на доске. – Сколько вершин у каждого из данных треугольников? – Назовите вершины в каждом треугольнике. Сосчитайте, сколько всего отмечено вершин. Почему получили 7, а не 9? | | ||
| 3. Маша ниже Веры, а Вера ниже Иры. Покажите на рисунке Машу, Веру и Иру. 4. Запишите выражения и найдите их значения. 15 увеличить на 4; 46 увеличить на 30; | | ||
37 уменьшить на 31; 61 уменьшить на 3;
48 уменьшить на 29; 90 уменьшить на 5;
3 увеличить на 38; 3 увеличить на 67.
II. Работа по учебнику.
Задание 1. Составьте выражения для ответа на вопросы задачи. Сколько голов участвовало в битве? (5 + 4 · 6 = 5 + 24 = 29.)
– Сколько всего лап у бойцов, если драконы были четырехлапые?
(5 · 2 + 4 · 4 = 10 + 16 = 26.)
– У драконов по два крыла. Сколько крыльев у орлов и драконов вместе? (5 · 2 + 4 · 2 = 10 + 8 = 18.)
– Что могут обозначать следующие выражения?
а) 5 + 4 = 9 (ж.) – было бойцов;
б) 2 · (5 + 4) = 2 · 9 = 18 (кр.) – всего крыльев.
– Прочитайте задачу 2. Что известно? Что требуется узнать? Решите задачу разными способами.
3 лошади – по 4 п.
4 ослика – по 4 п.
Всего – ?
I способ. II способ.
1) 4 · 3 = 12 (п.) – для лошадей; 1) 3 + 4 = 7 (жив.) – было;
2) 4 · 4 = 16 (п.) – для осликов; 2) 4 · 7 = 28 (п.) – всего.
3) 12 + 16 = 28 (п.) – всего.
Задание 3. Что означает каждое выражение?
а) 44 : 4 = 11 – животных подковал;
б) 44 : 4 – 8 = 11 – 8 = 3 – ослика подковал.
Задание 4. В реке нежились 18 крокодилов, 7 бегемотиков и множество черепах. Всего было 63 животных. Сколько было черепах?
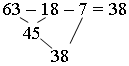
Задание 5. Сколько зеленых попугаев было на пальме?
(16 + 5) · 3 = 21 · 3 = 63.
– Что мы узнаем, выполнив такие вычисления?
16 + 5 + (16 + 5) · 3 = 21 + 63 = 84 (п.) – всего.
– Что можно узнать, выполнив такие вычисления?
(16 + 5) · 3 – (16 + 5) = 63 – 21 = 42 (п.) – больше зеленых, чем желтых и красных вместе.
Задание 6. Сколько всего котят?
(7 + 11 + 6) : 2 = 24 : 2 = 12 (к.) – всего.
Задание 7. Составьте выражение:
(82 – 40) : 6 = 42 : 6 = 7 (ж.).
– Сколько ножек у жуков? (6 ножек.)
Задание 8. Прочитайте. Что нужно найти в следующих задачах?
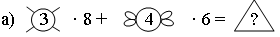
Число ножек у 3 пауков и 4 мух.
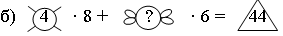
Число мух, если всего было 44 ног животных и среди них были ноги 4 пауков.
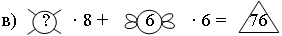
Число пауков, если всего было 76 ног животных и среди них были ноги 6 мух.
– Решите эти задачи, подобрав подходящие числа.
а) 3 · 8 + 4 · 6 = 48; б) 4 · 8 + 2 · 6 = 44;
в) 5 · 8 + 6 · 6 = 76.
III. Работа по карточкам.
– Проверьте, правильно ли решены примеры. Исправьте ошибки, которые вы найдете. Как бы вы оценили эти работы?
1) 52 – 36 : 12 = 49 8) 68 – 8 · 2 – 4 = 116
2) 104 + 5 · 4 = 124 9) 32 – 14 + (15 : 5 – 1) = 14
3) 48 + 32 : 16 = 50 10) 88 + 29 – 7 · 8 = 62
4) 54 : 3 – 16 = 2 11) 48 – (8 – 6 : 2) = 47
5) 50 + (18 – 8 : 2) = 55 12) 25 – 5 · 4 : 10 = 8
6) 26 – 6 : (62 – 60) = 10 13) 13 · 5 + 56 : 8 = 72
7) 59 – 3 · 15 = 14 14) 48 : 3 + 4 · 7 = 44
Урок 131
Действия с выражениями (повторение)
Цели деятельности учителя: способствовать формированию умения выполнять действия по порядку; содействовать совершенствованию умений выполнять действия с числами 0, 1, 10, составлять выражение по условию задачи, выполнять сложение и вычитание в пределах 100.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: оценивают собственную учебную деятельность; применяют правила делового сотрудничества: сравнивают различные точки зрения, считаются с мнением другого человека; проявляют терпение и доброжелательность в споре (дискуссии), доверие к соучастнику деятельности.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: оценивают уровень владения тем или иным учебным действием; анализируют результаты собственной деятельности; познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; проверяют информацию, находят дополнительную информацию, пользуясь справочной литературой; коммуникативные: оформляют диалогические высказывания, понимают позицию партнера, в том числе и отличную от своей, согласовывают действия с партнером, вступают в коллективное учебное сотрудничество.
Ход урока
I. Устный счет.
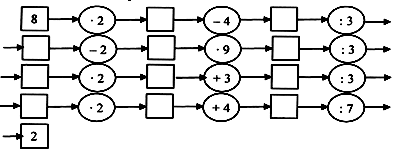
1. Заполните цепочку.
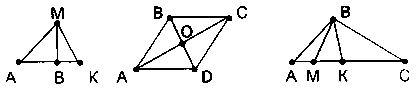
2. Сколько всего отрезков на каждом чертеже? Какие отрезки нужно сложить, чтобы получить отрезки АК, BD, АС?
3. В букете 4 желтые розы и 5 белых. Объясните, что обозначают равенства.
4 + 5 = 9 9 – 5 = 4
9 – 4 = 5 5 – 4 = 1
4. Поставьте знаки арифметических действий так, чтобы выполнялся данный порядок действий:

Дата: 2018-12-21, просмотров: 409.