Задание 4. Найдите значения выражений.
Задание 5. Сформулируйте правило деления числа 0 на любое число.
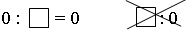
Делить на ноль нельзя!
Задание 6. Какой смысл могут иметь выражения, если человек делает покупки в магазине?
48 + 35 = 83 (р.) – стоит вся покупка;
100 – 24 = 76 (р.) – осталось;
9 · 6 = 54 (р.) – стоит 6 булочек.
– Какой смысл могут иметь выражения, если птицы садятся на провода?
7 + 9 + 5 = 21 (пт.) – всего;
23 – 4 = 19 (пт.) – осталось;
27 : 3 = 9 (пт.) – на одном проводе.
III. Фронтальная работа.
– Проведем опыт с числами. Напишите на карточках числа от 1 до 25 и выложите карточки подряд.
– Теперь некоторые карточки переверните по следующим правилам:
· Сначала перевернем каждую вторую карточку. Это значит, что карточки с числами 2, 4, 6... окажутся лежащими числом вниз.
· Затем перевернем на другую сторону каждую третью карточку. Понятно, что при этом некоторые карточки будут перевернутыми два раза. Они окажутся лежащими числом вверх, как и в начале.
– Какие числа были на дважды перевернутых карточках? (Числа 6, 12, 18, 24.)
· На следующем этапе мы перевернем каждую четвертую карточку. Как видите, карточка с числом 12 переворачивалась уже три раза.
– Какая еще карточка переворачивалась три раза? (Карточка 24.)
· Затем переворачивается каждая пятая карточка. Затем – каждая шестая, каждая седьмая и т. д. Наконец, на двадцать пятом этапе будет перевернута одна последняя карточка.
– Какие числа будут видны на карточках, когда мы закончим работу?
– Выпишите их.
– Как эти числа называются?
– А какие числа окажутся видны, если карточек будет не 25, а 100 (с числами от 1 до 100)? Понятно, что при этом переворачивать их мы будем дольше. На последнем этапе будет перевернута одна карточка.
IV. Итог урока.
– Как называются числа при делении?
– Сформулируйте правило деления с числом 0.
Урок 123
порядок действий в выражении без скобок
Цели деятельности учителя: способствовать ознакомлению с правилами выполнения действий в выражении без скобок; содействовать формированию умения решать текстовые задачи с помощью составления выражения.
Планируемые результаты образования.
Предметные: имеют представления о том, как составлять задачи с опорой на схемы, сопоставлять выражение с условием задачи; умеют определять порядок действий в выражениях без скобок, выполнять вычисления в несколько действий, сравнивать значения выражений, решать задачи на все арифметические действия; знают, как правильно использовать в речи названия выражений (сумма, разность, произведение, частное).
Личностные УУД: оценивают собственную учебную деятельность: свои достижения, самостоятельность, инициативу, ответственность, причины неудач.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: корректируют свою деятельность: вносят изменения в процесс с учетом возникших трудностей и ошибок; познавательные: выявляют (при решении различных учебных задач) известное и неизвестное; исследуют собственные нестандартные способы решения; коммуникативные: сотрудничают с товарищами при работе в паре; описывают объект: передают его внешние характеристики, используя выразительные средства языка.
Ход урока
I. Устный счет.
1. Расположите данные выражения в порядке убывания их значений:
420 : 60 480 : 80
36 : 6 350 : 70
240 : 80 45 : 5
2. Уменьшите числа:
а) 72, 56, 48, 24 в 8 раз; б) 18, 27, 12, 21 в 3 раза;
в) 42, 49, 21, 28 в 7 раз.
– Не выполняя вычислений, расположите данные выражения в порядке возрастания их значений:
27 + 30 27 + 33 20 + 30 25 + 30 33 + 29
3. Вставьте числа в «окошки», чтобы получились верные записи:
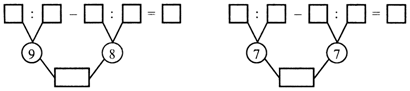
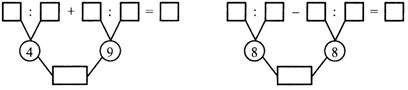
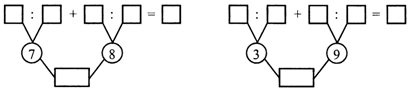
II. Сообщение темы урока.
– Сравните математические записи на доске:

– Сегодня на уроке будем учиться выполнять действия по порядку.
III. Работа по учебнику.
Задание 1. Выполните действия по порядку: слева направо.
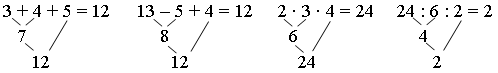
– А теперь попробуйте выполнить их в другом порядке.
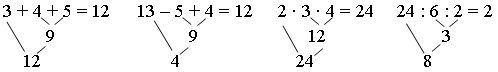
– Сравните результаты вычислений.
– Как вы думаете, важен ли порядок выполнения действий при вычислениях?
– Для того чтобы не было путаницы при вычислениях, соблюдают следующие правила:
• Сложение и вычитание выполняют в том порядке, в каком записаны действия: слева направо.
• Умножение и деление так же выполняют по порядку – слева направо.
• Если в выражении встречаются разные арифметические действия, то сначала выполняют умножение и деление, а затем сложение и вычитание.
Задание 2. Вычислите.
1 2 3
35 – 27 + 3 – 0 = 8 + 3 – 0 = 11 – 0 = 11.
1 2
67 – 38 – 13 = 29 – 13 = 16.
1 2 3
40 : 5 · 4 : 1 = 8 · 4 : 1 = 32 : 1 = 32.
1 2 3
6 · 3 : 2 · 5 = 18 : 2 · 5 = 9 · 5 = 45.
2 1 2 1
16 – 16 : 4 = 16 – 4 = 12. 48 + 2 · 6 = 48 + 12 = 60.
Задание 3. Как вычислить площадь составленной фигуры? Sобщ = = S1 + S2.
– Составьте выражение и найдите его значение.
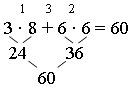
– Какая часть фигуры имеет меньшую площадь? (Зеленый прямоугольник.)
– На сколько меньшую? Составьте выражение для ответа на этот вопрос.
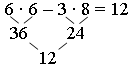
Задание 4. Определите порядок действия. Выполните действия.
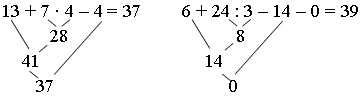
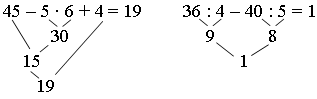
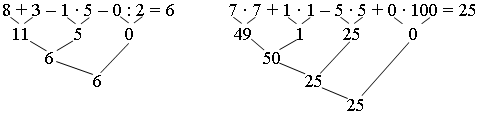
Задание 5. Составьте выражения для решения задач.
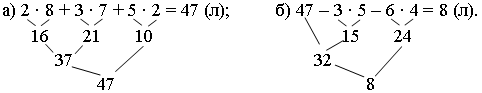
Задание 6 (работа в парах). Вспомните свойства противоположных сторон прямоугольника. (Противоположные стороны равны.)
– Составьте разными способами выражения для вычисления периметра прямоугольника.
4 + 4 + 14 + 14 = 36 4 · 2 + 14 · 2 = 36 14 · 2 + 4 · 2 = 36
IV. Фронтальная работа.
– Чтобы найти сумму 13 + 12 + 27 + 19 + 18 + 11, удобно переставить слагаемые, объединить их в пары (ведь от перемены мест слагаемых сумма не меняется!). Вот так:
13 + 12 + 27 + 19 + 18 + 11 = (13 + 27) + (12 + 18) + (19 + 11) = 40 + 30+ + 30 = 100.
– Попробуйте таким же образом, объединяя слагаемые в удобные пары, найти следующие суммы:
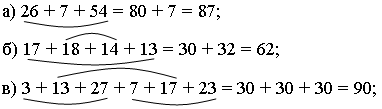
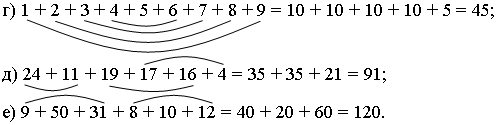
– Найдите сумму: 17 + 19 + 24 + 15 + 12 = 87.
– А как быстрее найти эти суммы?
18 + 20 + 24 + 16 + 13 = 87 + 1 + 1 + 1 + 1 + 1 = 91.
16 + 18 + 22 + 15 + 11 = 87 – 1 – 1 – 2 – 1 = 82.
19 + 21 + 25 + 17 + 14 = 87 + 2 + 2 + 1 + 2 + 2 = 96.
19 + 20 + 25 + 16 + 13 = 87 + 2 + 1 + 1 + 1 + 1 = 93.
20 + 21 + 26 + 17 + 15 = 87 + 3 + 2 + 2 + 2 + 3 = 99.
21 + 22 + 27 + 18 + 16 = 87 + 4 + 3 + 3 + 3 + 4 = 104.
V. Итог урока.
– Сформулируйте правила выполнения действий.
Урок 124
Составление выражения при решении задачи
Цель деятельности учителя: способствовать формированию умения выполнять вычисления в выражениях без скобок и решать текстовые задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как составлять задачи с опорой на схемы, сопоставлять выражение с условием задачи; умеют определять порядок действий в выражениях без скобок, выполнять вычисления в несколько действий, сравнивать значения выражений, решать задачи на все арифметические действия; знают, как правильно использовать в речи названия выражений (сумма, разность, произведение, частное).
Личностные УУД: применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнениями другого человека; проявляют терпение и доброжелательность в споре (дискуссии).
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: планируют решение учебной задачи: выстраивают последовательность необходимых операций (алгоритм действий); познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; приводят примеры в качестве доказательства выдвигаемых положений; коммуникативные: сотрудничают с товарищами при работе в паре; описывают объект: составляют небольшие устные монологические высказывания, «удерживают» логику повествования, приводят убедительные доказательства.
Ход урока
I. Устный счет.
1. Вставьте пропущенные цифры, чтобы равенства были верными:

2. Поставьте знаки действий и, если нужно, скобки так, чтобы получились верные равенства.
4 … 3 … 2 = 2 4 … 3 … 2 = 3 4 … 3 … 2 = 4
4 … 3 … 2 = 5 4 … 3 … 2 = 14 4 … 3 … 2 = 4
4 … 3 … 2 = 24 4 … 3 … 2 = 14 4 … 3 … 2 = 20
4 … 3 … 2 = 9 4 … 3 … 2 = 3
3. Расставьте порядок действий на каждой схеме:
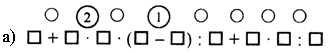
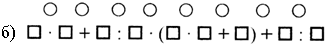
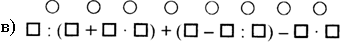
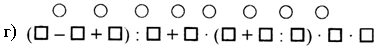
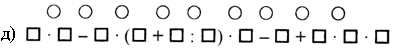
II. Работа по учебнику.
Задание 1. Запишите выражения, которые показывают длину различных дистанций.
а) 6 + 7 = 13 (км);
б) 8 · 3 = 24 (км);
в) 7 · 2 + 8 = 14 + 8 = 22 (км);
г) 7 + 6 · 2 = 7 + 12 = 19 (км);
д) 8 · 2 + 6 · 3 = 16 + 18 = 34 (км).
Задание 2. Расскажите словами, как тренировались велосипедисты. Сколько километров проехал каждый?
7 + 8 + 6 = 15 + 6 = 21 8 + 6 · 3 = 8 + 18 = 26
6 · 4 = 24 6 · 5 = 30
7 · 3 + 6 · 2 = 21 + 12 = 33 8 · 5 = 40
7 + 8 · 4 = 7 + 32 = 39 8 + 7 · 2 + 6 = 8 + 14 + 6 = 28
Задание 3. Запишите номер спортсмена, который проехал самую короткую дистанцию. (№ 1.)
– Кто проехал больше всех? (№ 7.)
– Запишите номера спортсменов в порядке возрастания длины их дистанции.
(№ 1, 2, 5, 8, 6, 3, 4, 7.)
Задание 4. Составьте план тренировки, при котором общая длина дистанции будет 20 км.
6 · 2 + 8 = 20 7 · 2 + 6 = 20
8 + 6 · 2 = 20 6 + 7 · 2 = 20
6 + 8 + 6 = 20 7 + 6 + 7 = 20
– Составьте разными способами план тренировки с общей длиной дистанции в 40 километров.

Задание 5. Сколько раз проехали велосипедисты каждый круг за два дня тренировки?
– Какова общая длина дистанции, которую проехал 1-й велосипедист за два дня?
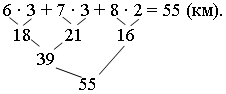
– Какова общая длина дистанции, которую проехал 2-й велосипедист за два дня?
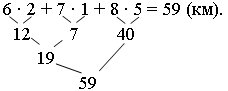
– Какова общая длина дистанции, которую проехал 3-й велосипедист за два дня?
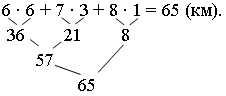
Задание 6. Поставьте в пустые клетки число кругов, которые нужно проехать велосипедисту, чтобы получилась следующая длина дистанции:
а) 18 км: 6 · 3 + 7 · 0 + 8 · 0 = 18;
б) 30 км: 6 · 5 + 7 · 0 + 8 · 0 = 30
6 · 0 + 7 · 2 + 8 · 2 = 30;
в) 36 км: 6 · 6 + 7 · 0 + 8 · 0 = 36
6 · 0 + 7 · 4 + 8 · 1 = 36
6 · 2 + 7 · 0 + 8 · 3 = 36;
г) больше 25 км, но меньше 30 км:
6 · 2 + 7 · 2 + 8 · 0 = 26
6 · 3 + 7 · 0 + 8 · 1 = 26
6 · 0 + 7 · 4 + 8 · 0 = 28.
Урок 125
Выражения со скобками
Цели деятельности учителя: способствовать ознакомлению с выражениями, содержащими скобки; содействовать формированию умения выполнять порядок действий в выражениях со скобками; создавать условия для совершенствования умения составлять равенства, используя шифр.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, на нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: выражают положительное отношение к процессу познания, проявляют внимание, желание больше узнать.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: контролируют выполнение вычислений в несколько действий; анализируют собственную работу; познавательные: наблюдают за изменением значения выражений в зависимости от наличия и места скобок; проверяют информацию, находят дополнительную информацию; пользуются справочным материалом в конце учебника (таблицей сложения, таблицей умножения, именным указателем); коммуникативные: сотрудничают с товарищами при работе в паре.
Ход урока
I. Устный счет.
1. Поставьте числа внутри прямоугольников так, чтобы по строчкам и по столбикам получились верные равенства.
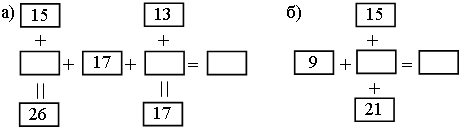
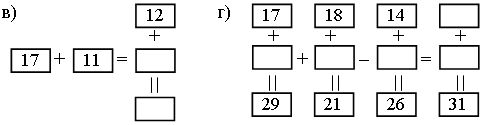
2. Найдите площадь закрашенной фигуры.
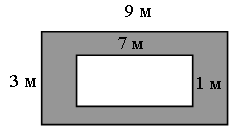
3. Поставьте скобки и обозначьте порядок выполнения действий так, чтобы получились верные равенства:



4. Игра «Распутай клубок».
25 + Δ = ○ ¶– Δ = 120
49 : Δ = Δ Δ : ○ = 4
○ · 8 = ¶ 100 + Δ = 120
¶ · Δ = 28 ○ · Δ = 100
¶ · ¶ = 16 ¶ : ♦ = Δ
II. Сообщение темы урока.
– Сравните математические записи на доске.
10 – 5 + 3 = 8 10 – (5 + 3) = 2
– Чем они похожи? Чем различаются? Сегодня на уроке будем находить значения выражений со скобками.
III. Работа по учебнику.
Задание 1. Что купила Аня? (Чашку и блюдце.) Сколько денег она заплатила? (17 + 13 = 30 (р.).)
– Что купила Вика? (Две чашки и два блюдца.) Сколько денег она заплатила? ((17 + 13) · 2 = 60 (р.).)
– Что купила Галя? (Чашку и два блюдца.) Сколько денег она заплатила? (17 + 13 · 2 = 43 (р.).)
– Что купила Даша? (Две чашки и два блюдца.) Сколько денег она заплатила? (17 · 2 + 13 · 2 = 60 (р.).)
– Кто сделал одинаковые покупки?
– Прочитайте правило в учебнике.
Задание 2. Выполните записи:
а) (17 + 13) · 6; б) (17 + 13) · 3 + 13 · 3;
в) 40 + 13 · 6 + (17 + 13) · 2.
Задание 3. В каком порядке надо вычислять значения выражений?
– Вычислите значения выражений:

– Сравните результаты.
– Вычислите значения выражений:

– Сравните результаты.
Задание 4. Составьте выражения и найдите их значения.
9 + 6 – 3 = 15 – 3 = 12 (9 – 6) – (3 – 2) = 3 – 1 = 2
6 · 2 – 9 = 12 – 9 = 3 6 · (9 – 3) = 6 · 6 = 36
2 + 9 : 3 = 2 + 3 = 5 9 · (6 : 3) = 9 · 2 = 18
(9 – 3) : 2 = 6 : 2 = 3 (6 : 2) · 9 = 3 · 9 = 27
Задание 5. Сколько было взрослых? (2 · 4.)
– Сколько было детей? (3 · 4.)
– Сколько человек отправились на пикник?
(2 · 4 + 3 · 4 или (2 + 3) · 4.)
– Что означают следующие выражения:
а) 2 + 3 = 5 (чел.) – в 1-й машине;
б) 2 · 4 = 8 (чел.) – взрослых всего;
в) 3 + 3 + 3 + 3 = 12 (чел.) – детей всего.
Задание 6. Составьте два выражения для вычисления площади прямоугольника разными способами.
6 · 3 + 3 · 3 = 18 + 9 = 27 (кв. см).
(6 + 3) · 3 = 9 · 3 = 27 (кв. см).
IV. Фронтальная работа.
– Чему равно значение этого выражения? (7 – 5 + 1 = 3.)
– Как изменится результат, если поставить скобки? (7 – (5 + 1) = 1.)
– Расставьте скобки так, чтобы равенства были верными:
17 – 10 + 5 – 1 = 11 Ответы: (17 – 10) + 5 – 1 = 11
17 – 10 + 5 – 1 = 1 17 – (10 + 5) – 1 = 1
17 – 10 + 5 – 1 = 3 17 – (10 + 5 – 1) = 3
– Расставьте скобки так, чтобы получилось число как можно больше:
31 – 13 + 7 – 5 + 1 Ответы: (31 – 13) + 7 – 5 + 1 = 21
31 – 13 – 7 – 5 – 1 31 – (13 – 7 – 5 – 1) = 31
– Расставьте скобки так, чтобы получилось число как можно меньше:
31 – 13 + 7 – 5 + 1 Ответы: 31 – (13 + 7) – (5 + 1) = 5
31 – 13 – 7 – 5 – 1 (31 – 13 – 7 – 5) – 1 = 5
V. Итог урока.
– Как выполнить действия в выражениях со скобками?
Урок 126
Порядок действий в выражении со скобками
Цель деятельности учителя: способствовать формированию умений выполнять порядок действий в выражениях со скобками, выбирать выражения для решения задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: оценивают собственную учебную деятельность; выражают положительное отношение к процессу познания.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: контролируют выполнение вычислений в несколько действий; оценивают весомость приводимых доказательств; анализируют эмоциональное состояние, полученное от успешной (неуспешной) деятельности; познавательные: наблюдают за изменением значения выражений в зависимости от наличия и места скобок; пользуются справочным материалом в конце учебника (таблицей сложения, таблицей умножения, именным указателем); исследуют собственные нестандартные решения; коммуникативные: сотрудничают с товарищами при работе в паре; доносят свою позицию до всех участников образовательного процесса.
Ход урока
I. Устный счет.
1. Какие знаки действий нужно вставить в «окошки», чтобы получить верные равенства?
9 · 3 = 9 □ 2 □ 9 24 · 1 = 8 □ 3 □ 1
9 · 5 = 9 □ 6 □ 9 72 · 0 = 0 □ 1 □ 72
8 · 5 = 5 □ 8 □ 1 8 · 8 = 8 □ 9 □ 8
2. В каждый пакет положили 5 пряников и 3 вафли. Сколько пряников и вафель положили в 7 пакетов?
3. У дедушки трое внуков. Когда он дал каждому из них 6 орехов, у него осталось 2 ореха. Сколько орехов было у дедушки?
4. Найдите площадь закрашенной фигуры.
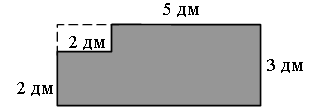
5. Поставьте скобки и расставьте порядок действий так, чтобы получились верные равенства:


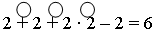
II. Работа по учебнику.
– Сегодня на уроке будем определять порядок действий в сложных выражениях.
Задание 1. Попробуйте определить, в каком порядке следует выполнять действия в этом выражении.
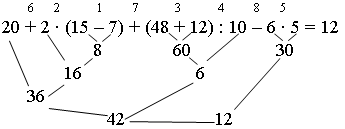
– Сформулируйте правило.
– Где выполняют действия первыми? (Действия в скобках.)
– Какие арифметические действия выполняются раньше? (Умножение и деление выполняют по порядку слева направо, а затем сложение и вычитание по порядку слева направо.)
Задание 2. Определите порядок выполнения вычислений. Каким правилом вы воспользовались?
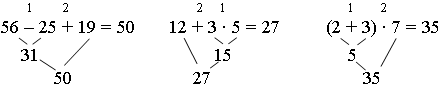
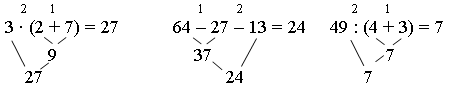
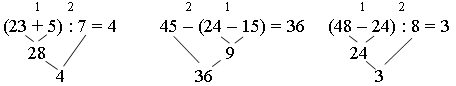
Задание 3. Найдите значения выражений и сравните результаты.
а) 100 – (60 – 15) = 100 – 45 = 55 б) (8 + 2) · 8 = 10 · 8 = 80
(100 – 60) – 15 = 40 – 15 = 25 8 + (2 · 8) = 8 + 16 = 24
в) (28 + 8) : 4 = 36 : 4 = 9
28 + (8 : 4) = 28 + 2 = 30
Задание 4. Составьте выражение по задаче.
3 · 10 + 1 · 2 = 30 + 2 = 32.
– Прочитайте задачу 5. Что известно? Что требуется узнать? Выберите выражение, подходящее для решения задачи. Объясните свой выбор.
7 · 3 – 3 · 1 = 21 – 3 = 18.
Задание 6 (работа в парах).
а) 47 + (26 + 14) = 47 + 40 = 87 д) 8 · (4 · 2) = 8 · 8 = 64
(47 + 26) + 14 = 73 + 14 = 87 (8 · 4) · 2 = 32 · 2 = 64
б) 47 – (26 – 14) = 47 – 12 = 35 е) 8 : (4 : 2) = 8 : 2 = 4
(47 – 26) – 14 = 21 – 14 = 7 (8 : 4) : 2 = 2 : 2 = 1
в) 47 + (26 – 14) = 47 + 12 = 59 ж) 8 · (4 : 2) = 8 · 2 = 16
(47 + 26) – 14 = 73 – 14 = 59 (8 · 4) : 2 = 32 : 2 = 16
г) 47 – (26 + 14) = 47 – 40 = 7 з) 8 : (4 · 2 ) = 8 : 8 = 1
(47 – 26) + 14 = 21 + 14 = 35 (8 : 4) · 2 = 2 · 2 = 4
Задание 7. В каком порядке надо выполнять действия?
– Выполните вычисления с помощью калькулятора.
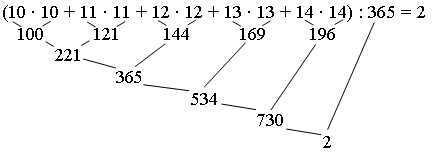
III. Итог урока.
– Сформулируйте правило определения порядка действий в сложном выражении.
Урок 127
Порядок действий в выражении со скобками
Цели деятельности учителя: создать условия для формирования понятия «равные выражения»; способствовать формированию умения находить значения выражений; содействовать совершенствованию умения решать текстовые задачи с помощью составления выражения.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: оценивают собственную учебную деятельность: свои достижения, самостоятельность, инициативу, ответственность, причины неудач.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: определяют и формулируют цели деятельности на уроке с помощью учителя; контролируют выполнение вычислений в несколько действий; оценивают весомость приводимых доказательств; познавательные: сравнивают различные объекты: выделяют из множества один или несколько объектов, имеющих общие свойства; наблюдают за изменением значения выражений в зависимости от наличия и места скобок; пользуются справочным материалом в конце учебника (таблицей сложения, таблицей умножения, именным указателем); коммуникативные: слушают и понимают речь других (одноклассников, учителя), решают совместно с соседом по парте поставленную задачу.
Ход урока
I. Устный счет.
1. В коробке 18 красных кубиков, а зеленых – на 2 больше, чем красных. Сколько всего красных и зеленых кубиков в коробке?
2. Выберите выражения, которые можно составить по данной задаче.
18 – 2 18 – 2 + 18 18 + 2 – 18
18 + 2 18 + 2 + 18 18 + 18 – 2
3. Догадайтесь, какие единицы длины пропущены, и запишите их.
а) Высота парты – 60 _____;
б) рост ученика – 1 ____ 30 ____;
в) высота трехэтажного дома – 10 ____;
г) рост Дюймовочки – 25____.
4. В коробке было 12 карандашей. Лена взяла из коробки сначала 3 карандаша, а потом еще 2. Сколько карандашей осталось в коробке?
II. Сообщение темы урока.
– Рассмотрите записи на доске.
8 · 5 36 + 4
54 – 4 80 : 2
– Чем они похожи? (Значения всех выражений равны 40.)
– Сегодня на уроке будем учиться находить равные выражения.
III. Работа по учебнику.
Задание 1. Запишите выражение, которое показывает, сколько пробежал первый спортсмен. (6 · 2 + 8 = 20 (км).)
– Сколько пробежал второй спортсмен? (5 · 4 = 20 (км).)
– Мы можем составить верное равенство. (6 · 2 + 8 = 5 · 4.)
– Два выражения равны, если они имеют одинаковые значения.
Задание 2. Выпишите выражения, которые имеют такое же значение, как выражение 5 · 4.
5 · 4 = 9 + 10 + 1 5 · 4 = 2 · 9 + 2
5 · 4 = 3 · 7 – 1 5 · 4 = 10 · (23 – 21)
5 · 4 = (3 · 7) · 2
Задание 3 (работа в парах).
Коля выполнил первое действие в каждом примере. Проверьте его записи. Исправьте ошибки, если они есть. Закончите вычисления.
а) 3 · 2 + 5 + 5 · 4 = 6 + 5 + 5 · 4 = 11 + 20 = 31;
б) 3 · (2 + 2) + 3 · 2 = 3 · 4 + 3 · 2 = 12 + 6 = 18;
в) 3 – 2 + 3 · 9 = 1 + 27 = 28.
Задание 4. Определите порядок действий и вычислите:
37 + 7 · 2 = 37 + 14 = 51 8 · 3 – 18 = 24 – 18 = 6
(43 – 7) : 4 = 36 : 4 = 9 8 · (88 – 80) = 8 · 8 = 64
5 · 7 + 15 = 35 + 15 = 50 (24 – 9) : 5 = 15 : 5 = 3
28 – 12 + 8 = 16 + 8 = 24 6 · 6 – 26 = 36 – 26 = 10
76 – 5 · 7 = 76 – 35 = 41 (35 – 28) · 5 = 7 · 5 = 35
(8 + 37) : 5 = 45 : 5 = 9 9 · (27 – 18) = 9 · 9 = 81
Задание 5. Составьте выражения для подсчета стоимости покупок.
1-й покупатель: 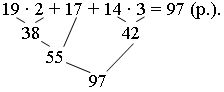
2-й покупатель: 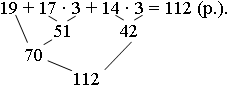
– Кому хватит 100 рублей? (Первому покупателю.)
Задание 6 (работа в парах).
– Вставьте по очереди в пустые клетки числа так, чтобы получить равные выражения.
– Проверьте работу друг друга.
6 · 6 = 4 · 9 39 – 34 = 25 : 5 4 · 7 = 50 – 22
5 · 9 = 69 – 24 9 + 9 = 45 – 27 2 + 5 = 28 : 4
40 – 22 = 3 · 6 24 + 16 = 8 · 5 5 · (11 – 2) = 9 · 5
Задание 7 (работа со справочной литературой).
| – Заполните пропущенные места или нарисуйте положение стрелок на часах. Коля Умнов проснулся утром в ____ часов. Ровно через 1 час он вышел из дома и пошел в школу. Первый урок в школе начинается в ___ часов___ минут. Уроки в школе заканчиваются в 12 часов дня. Коля остался в школе на дополнительные занятия. Эти занятия длились 1 час. После занятий Коля пошел домой и по дороге заглянул на стадион. Домой Коля пришел через 1 час после выхода из школы. Придя домой, Коля пообедал и в _____часа сел за уроки. Уроки Коля делал 2 часа и закончил их в ____ часов. Затем он два с половиной часа гулял, играл с ребятами в футбол. Когда он пришел домой, часы показывали _______. Вечером Коля отдыхал, смотрел телевизор полтора часа. Лег спать он в ____ часов вечера. |

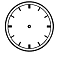


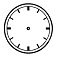





|
IV. Итог урока.
– Какие выражения называют равными?
Урок 128
Сравнение значений выражения
Цели деятельности учителя: способствовать формированию умения использовать знак умножения при записи суммы одинаковых слагаемых, применять перестановку множителей при вычислениях; содействовать совершенствованию умений восстанавливать равенства, решать текстовые задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: оценивают собственную учебную деятельность; выражают положительное отношение к процессу познания.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: контролируют выполнение вычислений в несколько действий; оценивают весомость приводимых доказательств; анализируют эмоциональное состояние, полученное от успешной (неуспешной) деятельности; познавательные: наблюдают за изменением значения выражений в зависимости от наличия и места скобок; пользуются справочным материалом в конце учебника (таблицей сложения, таблицей умножения, именным указателем); исследуют собственные нестандартные решения; коммуникативные: сотрудничают с товарищами при работе в паре; доносят свою позицию до всех участников образовательного процесса.
Ход урока
I. Устный счет.
1. Математический диктант.
а) Делимое 16. Делитель 2. Чему равно частное?
б) Чему равно частное чисел 9 и 9?
в) Назовите частное чисел 24 и 8.
г) Частное двух чисел равно 7. Делимое 21. Чему равен делитель?
| 2. Сколько квадратов на чертеже? – Сколько других многоугольников? – Сколько всего многоугольников? – Уберите одну палочку так, чтобы осталось 4 квадрата. | 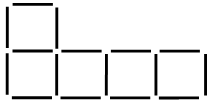
|
– Уберите одну палочку так, чтобы осталось 3 квадрата.
– Уберите две палочки так, чтобы осталось 4 квадрата. Найдите разные решения.
– Уберите две палочки так, чтобы осталось 3 квадрата.
3. Люда нашла 10 белых грибов, а Артем – на 3 гриба меньше. Найдите и подчеркните вопрос к этому условию, при ответе на который задача будет решаться в 2 действия:
а) Сколько грибов нашел Артем?
б) На сколько больше грибов нашла Люда, чем Артем?
в) Сколько всего грибов нашли Люда и Артем?
II. Работа по учебнику.
– Сегодня на уроке будем сравнивать выражения.
Задание 1. Запишите выражение, которое показывает, сколько заплатил Коля. (5 · 4 = 20 (р.).)
– Сколько заплатил Вася? (5 · 8 = 40 (р.).)
– Кто заплатил больше? (Вася.)
– Можно записать так: 4 · 5 < 8 · 5.
– На сколько больше рублей заплатил за покупку Вася, чем Коля?
(5 · 8 – 5 · 4 = 40 – 20 = 20 (р.).)
Задание 2. У какого выражения значение больше? Постарайтесь определить это без вычислений.
6 · 8 > 6 · 7 4 · 7 + 5 < 5 · 7 + 5
9 · 4 > 8 · 4 9 · 8 – 13 > 8 · 8 – 13
9 · 7 < 10 · 7 65 – 23 < 65 – 20
12 + 6 · 6 < 13 + 4 · 9 6 · (9 – 3) < 6 · (9 · 2)
Задание 3. Сравните выражения, поставив знак «>», «<» или «=».
5 · 5 > 3 · 8 46 – 18 < 7 · 5
16 + 34 = 14 + 36 5 · 10 < 25 + 27
Задание 4. Проверьте, какие равенства верны, а какие нет.
(8 + 7) · 3 > 8 + 7 · 3 – неверно.
10 · 2 > 30 · 1 – неверно.
34 – 17 · 2 > (34 – 17) · 2 – неверно.
1 · 65 + 0 · 35 > 0 · 65 + 1 · 35 – неверно.
Задание 5. Решите, сколько очков получил первый стрелок.
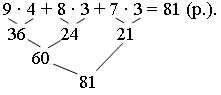
– Сколько очков получил второй стрелок?
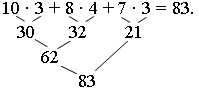
– Кто получил больше очков? (Второй стрелок.)
– На сколько больше? (83 – 81 = 2.)
Задание 6. На сколько площадь квадрата со стороной 7 клеток меньше площади квадрата со стороной 8 клеток?
(8 · 8 – 7 · 7 = 64 – 49 = 15.)
– Как по рисунку сосчитать это число, не находя площади квадратов?
(8 + 7 = 15.)
Задание 7. Значение какого выражения больше и на сколько?
а) 48 + 15 < 48 + 18 (на 3); г) 7 · 8 < 7 · 9 (на 7);
б) 37 – 22 > 37 – 29 (на 7); д) (5 + 2) · 6 > 4 · 6 (на 18);
в) 53 – 35 < 63 – 35 (на 10); е) 3 · 7 + 8 < 5 · 7 + 8 (на 14).
Задание 8. Какие часы показывают самое раннее время? (14 ч 20 мин.)
– Расположите часы по порядку от меньшего времени к большему.
14 ч 20 мин; 14 ч 30 мин; 14 ч 50 мин; 15 ч 00 мин.
– Одни часы опережают другие на 10 минут. Какие это часы? (14 ч 20 мин; 14 ч 30 мин; 14 ч 50 мин; 15 ч 00 мин.)
– Известно, что одни часы показывают время правильно. Другие спешат на 20 минут. Третьи отстают на 10 минут. А четвертые вообще стоят. Какие часы показывают время правильно? (14 ч 30 мин.)
– Какие часы стоят? (15 ч 00 мин.)
Задание 9. Запишите выражения из каждого столбика в порядке возрастания их значений.
а) 11 · 4 6 · 11 8 · 11 9 · 11
б) (5 – 3) · 8 3 · 8 5 · 8 2 · 3 · 8
в) 5 · 7 · 8 5 · 7 · 9 6 · 7 · 9
г) 4 · 5 · 5 3 · 5 · 6
III. Работа по карточкам.
– Вычислите:
а) 100 – 1 = в) 100 – (100 – (100 – 1)) =
б) 100 – (100 – 1) = г) 100 – (100 – (100 – (100 – 1))) =
– Можно ли теперь сообразить и сразу сказать, чему равно вот такое выражение:
100 – (100 – (100 – (100 – (100 – (100 – (100 – 1)))))) =
А если число 100 встретится 100 раз?
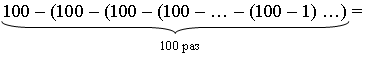
– Найдите удобный способ вычисления:
а) 43 + 59 – 42 =
б) 38 + 19 – 37 + 21 – 18 – 20 =
в) (11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20) – (1 + 2 + 3 + 4 + 5 + + 6 + 7 + 8 + 9 + 10) =
г) (2 + 4 + 6 + … + 100) – 1 + 3 + 5 + … + 99) =
IV. Итог урока.
– Какие выражения называют равными?
Урок 129
Сочетательные законы сложения и умножения
Цели деятельности учителя: способствовать ознакомлению с сочетательным законом сложения и умножения; содействовать формированию умений вычислять значения выражений удобным способом, применять сочетательный закон сложения и умножения, вычислять площади фигур.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия выражений и их компонентов; умеют определять порядок действий в выражениях со скобками, выполнять вычисления в несколько действий, сравнивать значения выражений, группировать слагаемые (множители) для рациональных вычислений, решать задачи в два действия на нахождение произведения, деления на части и по содержанию, нахождение суммы и остатка, на увеличение / уменьшение в несколько раз, разностное сравнение; знают, как сопоставлять выражение с условием задачи, составлять выражения для решения задачи разными способами.
Личностные УУД: применяют правила делового сотрудничества: сравнивают различные точки зрения, считаются с мнением другого человека; проявляют терпение и доброжелательность в споре (дискуссии), доверие к соучастнику деятельности.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: удерживают цель деятельности до получения ее результата; планируют решение учебной задачи, выстраивают последовательность необходимых операций; познавательные: анализируют результаты вычислений; воспроизводят по памяти информацию, необходимую для решения учебной задачи; коммуникативные: доносят свою позицию до всех участников образовательного процесса.
Ход урока
I. Устный счет.
1. Математический диктант.
– На сколько 16 больше 7? На сколько 8 меньше 20? Во сколько раз 24 больше 3? Во сколько раз 4 меньше 20?
2. Назовите число, которое: а) больше числа 7 в 3 раза; б) меньше числа 36 в 9 раз; в) больше числа 4 на 8; г) меньше числа 9 на 3.
3. Среди написанных здесь трех чисел надо найти два числа, сумма которых делится на 3.
а) 17; 24; 31; б) 18; 19; 20; в) 29; 8; 1.
4. Проведите оси симметрии:
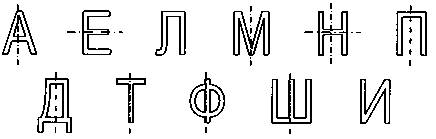
5. Туловище гигантского японского краба достигает 60 см, а есть крабы-горошины с размером тела в 2 см. Во сколько раз туловище краба-гиганта больше краба-горошины?
II. Работа по учебнику.
– Сегодня на уроке будем учиться находить значение суммы и значение произведения удобным способом.
Задание 1. Что могут означать выражения: (34 + 15) + 27; 34 + (15 + + 27)? (Это количество приключений.)
– Сравните значения этих выражений.
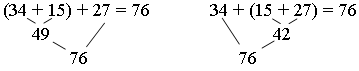
Задание 2 (работа в парах). Выберите по три числа и подставьте их в схему.
(○ + Δ) + □ = ○ + (Δ + □) (3 + 4) + 5 = 3 + (4 + 5)
– Проверьте, верные ли равенства вы получили.
– Эта схема выражает сочетательный закон сложения: при вычислениях слагаемые можно объединять в группы.
Задание 3. Вычислите, применяя сочетательный закон сложения.
(24 + 45) + 15 = 24 + (45 + 15) = 24 + 60 = 84
23 + (27 + 36) = (23 + 27) + 36 = 50 + 36 = 86
(63 + 28) + 12 = 63 + (28 + 12) = 63 + 40 = 103
Задание 4. Вычислите удобным способом.
24 + 17 + 33 = 24 + (17 + 33) = 24 + 50 = 74
15 + 43 + 12 + 7 = (15 + 12) + (43 + 7) = 27 + 50 = 77
28 + 16 + 32 = (28 + 32) + 16 = 60 + 16 = 76
Задание 5. Множители при вычислениях тоже можно объединять в группы. Это выражает сочетательный закон умножения.
(○ · □) · Δ = ○ · (□ · Δ)
– Вычислите, применяя сочетательный закон умножения.
(7 · 2) · 5 = 7 · (2 · 5) = 7 · 10 = 70
2 · (5 · 9) = (2 · 5) · 9 = 10 · 9 = 90
(4 · 4) · 5 = 4 · (4 · 5) = 4 · 20 = 80
Задание 6. Сосчитайте значения выражений рациональным способом.
5 · (3 · 4) = (5 · 4) · 3 = 20 · 3 = 60
3 · (5 · 5) = 3 · 25 = 75
2 · 3 · 5 · 3 = (2 · 5) · (3 · 3) = 10 · 9 = 90
2 · 2 · 2 · 5 = (2 · 5) · (2 · 2) = 10 · 4 = 40
Задание 7. Определите порядок действий и вычислите.
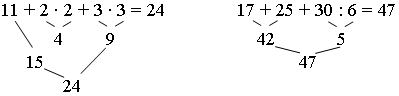
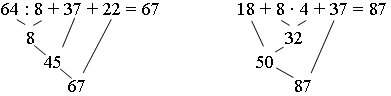
Задание 8. Составьте выражение для подсчета площади нового загона для первого дракона. (2 · 3 · 4 = 6 · 4 = 24 (кв. км).)
– Составьте выражение для подсчета площади нового загона для второго дракона. (3 · 4 · 2 = 12 · 2 = 24 (кв. км).)
– Сравните значения этих выражений.
Задание 9. Составьте разные выражения для вычисления площади фигуры.
7 · 5 + 3 · 3 + 7 · 5 = 35 + 9 + 35 = 79
7 · 5 · 2 + 3 · 3 = 70 + 9 = 79
17 · 5 – 3 · 2 = 85 – 6 = 79
Задание 10. Проверьте, верны ли равенства:
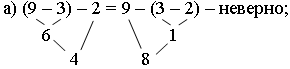
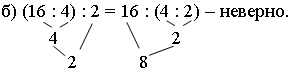
– Бывают ли сочетательные законы для вычитания и деления? (Не бывают.)
Дата: 2018-12-21, просмотров: 444.