Сумма двух чётных чисел – всегда чётное число.
Сумма двух нечётных чисел также всегда чётное число.
Сумма же чётного и нечётного чисел – число нечётное.
– Подчеркните чётные числа красным карандашом, а нечётные – синим: 8; 17; 23; 14; 72; 33; 56; 100; 99; 1.
– Понятно, что если последняя цифра числа чётная, то и само число – чётное. Цифру 0 мы считаем чётной. Если же последняя цифра – нечётная, то и число – нечётное.
– Не вычисляя сумм, скажите, чётные они или нечётные.
а) 117 + 3 + 96. (Эта сумма чётная.)
б) 10 + 11 + 12 + 13 + 14 + 15. (Эта сумма нечётная.)
1 + 11 + 111 + 1111 + 11111. (Эта сумма нечётная.)
– Чётной или нечётной является сумма пяти нечётных слагаемых? Трех нечётных и двух чётных?
– Сумма одиннадцати нечетных чисел является числом чётным или нечётным?
V. Итог урока.
– Как выполнить сложение с числом 0?
– Как выполнить сложение с числом 1?
– Сформулируйте правило умножения на 1.
– Сформулируйте правило умножения числа на 0.
Урок 121
Вычитание и деление
Цели деятельности учителя: способствовать ознакомлению с действиями вычитания и деления, обратных сложению и умножению; содействовать развитию умений решать и составлять обратные задачи, вычислять и записывать обратные действия, придумывать задачу по рисунку, выполнять проверку вычисления.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия компонентов арифметических действий; умеют сопоставлять свойства сложения и умножения (переместительные законы, действия с числами 0 и 1), выполнять вычисления в 2–3 действия (без скобок), решать задачи на все арифметические действия, составлять взаимообратные задачи.
Личностные УУД: воспринимают речь учителя (одноклассников), непосредственно не обращенную к учащемуся; оценивают собственную учебную деятельность.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: корректируют свою деятельность с учетом допущенных ошибок; анализируют собственную работу; познавательные: выявляют (при решении различных учебных задач) известное и неизвестное; исследуют закономерности при выполнении действий с четными и нечетными числами; коммуникативные: составляют небольшие устные монологические высказывания, «удерживают» логику повествования, приводят убедительные доказательства.
Ход урока
I. Устный счет.
1. Разгадайте правило, по которому составлены схемы, и вставьте числа в «окошки»:


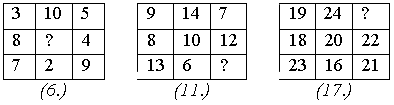
2. Сложите числа в каждой строке, в каждом столбце. Назовите пропущенные числа.
3. В классе 8 мальчиков, а девочек в 2 раза больше. На какие вопросы вы сможете ответить, выполнив действия:
8 · 2; 8 · 2 + 8; 8 · 2 – 8?
4. Соедините изображения, значения которых одинаковы.
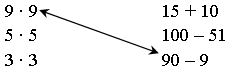
4 · 4 90 : 10
7 · 7 20 – 4
8 · 8 4 · 9
6 · 6 640 : 10
II. Сообщение темы урока.
– Рассмотрите записи на доске.
а) ▲▲▲Δ Δ Δ Δ; б) 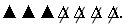
– Какие действия здесь изображены? (Сложение и вычитание.)
– Как называются эти действия? (Это обратные действия.)
– Сегодня на уроке будем учиться записывать обратные действия.
III. Работа по учебнику.
Задание 1. Как называется действие, обратное сложению? (Вычитание.) Какое действие обратно умножению? (Деление.)
Задание 2. Подберите числа так, чтобы получились верные равенства. Запишите, как найти эти числа.
а)  + 13 = 21 б) 68 –
+ 13 = 21 б) 68 –  = 44 в)
= 44 в)  · 8 = 32 г) 45 :
· 8 = 32 г) 45 :  = 5
= 5
21 – 13 = 8 68 – 44 = 24 32 : 8 = 4 45 : 5 = 9
8 + 13 = 21 68 – 24 = 44 4 · 8 = 32 45 : 9 = 5
Задание 3. Вычислите. Запишите обратные действия.
а) 34 + 62 = 96 б) 9 · 4 = 36
96 – 34 = 62 36 : 9 = 4
96 – 62 = 34 36 : 4 = 9
Задание 4. Какие правила показывают схемы?

– Подберите числа для каждой схемы. Запишите равенства.
15 – 0 = 15 15 – 15 = 0 15 : 1 = 15 15 : 15 = 1
Задание 5 (работа в парах). Придумайте задачу. Выберите два числа.
Число ёлок – 8 д. Решение:
Число берёз – 9 д. 8 + 9 = 17 (д.).
Всего – ? д.
– Какие еще можно составить задачи?
– Составьте обратные задачи.
Задание 6. Как найти число всех прыжков? (Число прыгунов умножить на число попыток.)
– Придумайте задачу, в которой нужно найти число прыгунов.
1 прыгун – 5 попыток. Решение:
? прыгунов – 45 попыток. 45 : 5 = 9 (пр.).
– Придумайте задачу, в которой будет неизвестно число прыжков каждого прыгуна.
1 прыгун – ? попыток. Решение:
9 прыгунов – 45 попыток. 45 : 9 = 5 (п.).
Задание 7. Вычислите и выполните проверку с помощью обратного действия.
Задание 8. Найдите количество вагонов. 72 : 9 = 8 (в.).
– Сформулируйте задачу, в которой нужно найти длину одного вагона.
8 вагонов – 72 см. Решение:
1 вагон – ? см. 72 : 8 = 9 (см).
– Какую еще можно составить задачу?
8 вагонов – ? см. Решение:
1 вагон – 9 см. 8 · 9 = 72 (см).
Задание 9. Составьте обратные задачи.
а) 1-й участник – 4 п. Решение:
7 участников – ? п. 4 · 7 = 28 (п.).
б) 1-й участник – ? п. Решение:
7 участников – 28 п. 28 : 7 = 4 (п.).
в) 1-й участник – 4 п. Решение:
? участников – 28 п. 28 : 4 = 7 (уч.).
IV. Итог урока.
– Назовите действие, обратное сложению (умножению).
Урок 122
Выражения
Цели деятельности учителя: способствовать ознакомлению с понятием «значение выражения»; создать условия для повторения названия компонентов сложения, умножения, вычитания, деления; содействовать формированию умений вычислять значения выражения, делить на 0, составлять выражения по решению задач и решать текстовые задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как составлять задачи с опорой на схемы, сопоставлять выражение с условием задачи; умеют определять порядок действий в выражениях без скобок, выполнять вычисления в несколько действий, сравнивать значения выражений, решать задачи на все арифметические действия; знают, как правильно использовать в речи названия выражений (сумма, разность, произведение, частное).
Личностные УУД: выражают положительное отношение к процессу познания, проявляют внимание, желание больше узнать.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: оценивают весомость приводимых доказательств и рассуждений; познавательные: воспроизводят по памяти информацию, необходимую для решения учебной задачи; коммуникативные: сотрудничают с товарищами при работе в паре.
Ход урока
I. Устный счет.
1. Арифметический диктант.
а) Число 5 увеличьте в 3 раза.
б) Число 15 уменьшите в 3 раза.
в) Сколько девяток нужно взять, чтобы получить 54?
г) Найдите частное 56 и 8.
д) На сколько 27 меньше 98?
е) Сколько восьмерок надо взять, чтобы получить 72?
ж) Найдите разность чисел 30 и 17.
з) Во сколько раз 3 меньше, чем 27?
2. Подставьте вместо квадратов такие цифры, чтобы получились верные равенства:
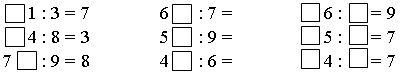
3. Когда из вазы 5 человек взяли по 3 сливы, то в ней осталось еще 5 слив. Сколько слив было в вазе?
– Выберите схему, которая соответствует условию задачи.

– Что обозначают данные выражения?
3 · 5 3 · 5 + 5 3 · 4 3 · 5 – 3 · 3
4. Продолжите ряд чисел:
309, 319, 329, ... 92, 83, 74, 65, … 291, 282, 273, ...
II. Работа по учебнику.
– Если соединить два числа знаком арифметического действия, то получится выражение.
Выражения называются так же, как результаты действий.

Сумма Разность

Произведение Частное
Задание 1. Вычислите и запишите равенства.
23 + 35 = 58 2 · 15 = 30
60 – 24 = 36 81 : 9 = 9
– Как называются числа при сложении? При делении?
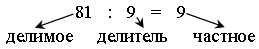
Задание 2. Составьте выражения для решения задач:
а) 32 + 48 = 80; в) 20 · 4 = 80;
б) 64 – 48 = 16; г) 100 : 10 = 10.
Задание 3. На тарелке 4 яблока. Разделите их на четверых поровну. Сколько получит каждый? (4 : 4 = 1 (ябл.).)
– На тарелке 0 яблок. Разделите это число яблок на 4. Сколько получит каждый? (0 : 4 = 0 (ябл.).)
– Запишите значения выражений.
0 : 1 = 0 0 : 7 = 0
0 : 10 = 0 0 : 55 = 0
– Как вы думаете, имеет ли смысл выражение 4 : 0? (Не имеет.)
– Вспомните и обобщите правило деления нуля.
0 : 2 = 0, так как 0 · 2 = 0.
0 : 8 = 0, так как 0 · 8 = 0.
Дата: 2018-12-21, просмотров: 415.