Задание 1. Посчитайте по цепочке.
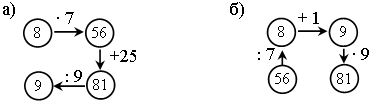
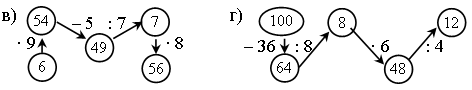
Задание 2. Сколько клеток в фигуре?
а) 3 · 6 + 2 · 3 = 18 + 6 = 24;
б) 7 · 6 + 4 · 2 = 42 + 8 = 50;
в) 3 · 7 + 4 · 4 = 21 + 16 = 37;
г) 11 · 9 – 8 · 2 – 2 – 3 = 99 – 16 – 2 – 3 = 83 – 2 – 3 = 81 – 3 = 78.
Задание 3. Выберите числа, которые делятся
а) на 4: 8, 32, 28, 36; в) на 7: 21, 63, 28, 14;
б) на 6: 12, 48, 30, 54; г) на 9: 27, 81, 45, 72.
Задание 4. Сколько прямоугольников голубого цвета уместится в розовом прямоугольнике?
а) 24 : 6 = 4; в) 56 : 7 = 8;
б) 48 : 8 = 6; г) 63 : 9 = 7.
Задание 5. Найдите произведения одинаковых чисел.
а) 10 <  ·
·  < 30;
< 30;
10 < 4 · 4 < 30 и 10 < 5 · 5 < 30;
б) 20 <  ·
·  < 50;
< 50;
20 < 5 · 5 < 50 и 20 < 6 · 6 < 50 и 20 < 7 · 7 < 50;
в) 30 <  ·
·  < 70;
< 70;
30 < 6 · 6 < 70 и 30 < 7 · 7 < 70 и 30 < 8 · 8 < 70;
г) 30 <  ·
·  < 70
< 70
40 < 7 · 7 < 90 и 40 < 8 · 8 < 90 и 40 < 9 · 9 < 90.
Задание 6. Сколько существует способов составить одну танцевальную пару? (16.)
а) Из четырех девочек. (6 способов.)
б) Из пяти мальчиков. (10 способов.)
в) Пары «мальчик – девочка» из четырех мальчиков и четырех девочек.
Ответ:
| Мальчик Девочка | 1 | 2 | 3 | 4 |
| 1 | + | + | + | + |
| 2 | + | + | + | + |
| 3 | + | + | + | + |
| 4 | + | + | + |
г) Любые пары из четырех мальчиков и четырех девочек. (28 способов.)
III. Фронтальная работа.
Задание 1. На столе лежат 3 кучки спичек. Из них составляется одна общая кучка. Можно ли теперь разложить эту кучку на две с одинаковым числом спичек?
В таблице слева указано число спичек, а справа надо написать слово «можно» или «нельзя».
| Число спичек в кучках | Можно ли разложить на две одинаковые кучки |
| 3; 4; 7 | Можно (3 + 4 + 7 = 14; 14 : 2 = 7) |
| 5; 7; 9 | Нельзя (5 + 7 + 9 = 21) |
| 6; 8; 29 | Нельзя (6 + 8 + 29 = 43) |
| 19; 37; 91 | Нельзя (19 + 37 + 91 = 147) |
Задание 2. Числа 1, 17, 33, 49 можно разбить на две группы с одинаковыми суммами. Как это сделать?
1 + 49 = 33 + 17
50 = 50
– А числа 6, 18, 28, 41 нельзя разбить на две группы с одинаковыми суммами.
а) 3, 5, 7, 9; б) 1, 2, 3, 4, 5, 6, 7;
3 + 9 = 5 + 7 2 + 3 + 4 + 5 = 1 + 6 + 7
12 = 12 14 = 14
в) 1, 2, 9, 25, 49, 64;
1 + 25 + 49 = 2 + 9 + 64
75 = 75
Урок 119
переместительные законы Сложения и умножения
Цели деятельности учителя : способствовать ознакомлению с переместительным законом сложения и умножения; содействовать развитию умения выбирать арифметическое действие в соответствии со смыслом текстовой задачи.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия компонентов арифметических действий; умеют сопоставлять свойства сложения и умножения (переместительные законы, действия с числами 0 и 1), выполнять вычисления в 2–3 действия (без скобок), решать задачи на все арифметические действия, составлять взаимообратные задачи.
Личностные УУД: имеют желание учиться; применяют правила делового сотрудничества: сравнивают разные точки зрения; считаются с мнением другого человека; проявляют терпение и доброжелательность.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: оценивают результаты своей и чужой деятельности, сравнивают ее с эталоном; познавательные: анализируют и фиксируют результаты своей деятельности; исследуют математические закономерности при выполнении действий с четными и нечетными числами; коммуникативные: сотрудничают с товарищами при работе в паре.
Ход урока
I. Устный счет.
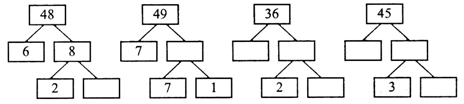
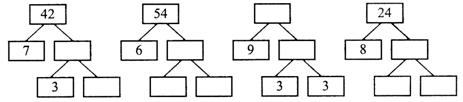
1. Разгадайте правило, по которому составлены схемы, и вставьте числа в «окошки»:
2. В каждой строке найдите «лишнее» число:
· 40, 35, 30, 24, 25, 20;
· 45, 54, 63, 64, 72, 81;
· 36, 32, 28, 27, 24, 20.
| 3. Выберите условие, которое соответствует схеме. а) Продали 4 ящика яблок по 7 кг каждый. б) Продали 4 ящика яблок и 7 кг груш. в) Продали 7 ящиков яблок по 4 кг каждый. – Задайте вопрос к выбранному условию и решите задачу. | 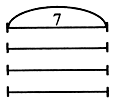
|
4. Разгадайте правила, по которым составлены ряды чисел. Вставьте пропущенные числа.
а) 9, 7, ... , 3, 1.
б) 11, 14, 17, 20, ... , 26.
в) 151, 251, 351, ... , 551, 651.
– Как называются числа первого ряда? Второго ряда? Третьего ряда? (Однозначные, двузначные, трехзначные.)
II. Сообщение темы урока.
– Рассмотрите записи на доске:
Δ + ○ = ○ + Δ Δ · ○ = ○ · Δ
– Какие законы они изображают?
– Сегодня на уроке будем использовать законы сложения и умножения.
III. Работа по учебнику.
Задание 1. Сколько шашек на каждом рисунке? (а) 8 + 3 = 11; б) 8 · 3 = 24.)
– Какие действия над числами 3 и 8 нужно совершить, чтобы ответить на вопрос?
– Как называются числа при сложении?
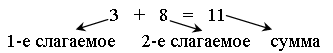
– Как называются числа при умножении?
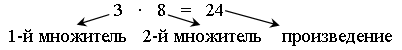
Задание 2. В каких случаях результаты вычислений будут одинаковы?
а) 20 + 4 = 24 20 · 4 = 80
20 – 4 = 16 20 : 4 = 5
4 + 20 = 24 4 · 20 = 80
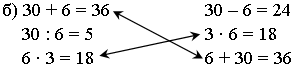
– Сформулируйте переместительный закон сложения.
– Сформулируйте переместительный закон умножения.
Задание 3 (работа в парах). Составьте равенства к схемам.
а) □ + ○ = ○ + □ б) â · ¶ = ¶ · â
100 + 9 = 9 + 100 11 · 15 = 15 · 11
25 + 72 = 72 + 25 98 · 17 = 17 · 98
36 + 98 = 98 + 36 23 · 44 = 44 · 23 и т. д.
Задание 4. В каждом столбике найдите выражения, значения которых одинаковы.
4 · 8 + 10 = 32 + 10 = 42 8 + 3 · 7 = 8 + 21 = 29
8 · 4 – 10 = 32 – 10 = 22 7 + 8 · 3 = 7 + 24 = 31
8 · 4 + 10 = 32 + 10 = 42 8 + 7 · 3 = 8 + 21 = 29
8 · 10 + 4 = 80 + 4 = 84 8 · 7 + 3 = 56 + 3 = 59
5 · 6 – 8 = 30 – 8 = 22
5 + 6 · 8 = 5 + 48 = 53
6 · 5 + 8 = 30 + 8 = 38
6 · 5 – 8 = 30 – 8 = 22
Задание 5. Прочитайте задачи и решите их.
а) Бальные платья – 8 нед. Решение:
Костюмы – 4 нед. 8 + 4 = 12 (нед.).
Всего – ? нед.
б) 1 неделя – 8 к. Решение:
4 недели – ? к. 8 · 4 = 32 (к.).
Задание 6 (работа в парах).
51 = 17 + 34 51 = 25 + 26 51 = 28 + 23
Задание 7. Заполните всеми возможными способами пустые клетки:
а) 4  + 3
+ 3  = 85 б) 2
= 85 б) 2  + 3
+ 3  = 54
= 54
49 + 36 = 85 20 + 34 = 54
48 + 37 = 85 21 + 33 = 54
47 + 38 = 85 22 + 32 = 54
47 + 38 = 85 23 + 31 = 54
46 + 39 = 85 24 + 30 = 54
в) 5 ·  =
=  г) 4 ·
г) 4 ·  =
=  8
8
5 · 2 = 10 4 · 7 = 28
5 · 4 = 20
5 · 6 = 30
5 · 8 = 40
IV. Фронтальная работа.
Задание 1. Три друга – Алик, Боря и Вася – живут на одной улице и даже на одной стороне этой улицы.
Между домами Алика и Бори есть еще 3 других дома. А между домами Бори и Васи 9 других домов.
Сколько домов находится между домами Алика и Васи?

Решение: 3 + 1 + 9 = 13 (д.).

Решение: 3 + 1 + 6 = 10 (д.).
Задание 2. Вдоль шоссе стоят три дерева: береза, тополь и дуб. Расстояние между березой и тополем равно 23 м, а между тополем и дубом – 47 м. Чему равно расстояние между березой и дубом?
– Найдите все случаи; для каждого сделайте рисунок.


Урок 120
Сложение и умножение с цифрами 0 и 1
Цели деятельности учителя: способствовать составлению правил сложения и умножения с числами 0 и 1; содействовать развитию умения выполнять действия с нолем и единицей; создать условия для совершенствования умений решать текстовые задачи, составлять равенства по рисункам.
Планируемые результаты образования.
Предметные: имеют представления о том, как правильно использовать в речи названия компонентов арифметических действий; умеют сопоставлять свойства сложения и умножения (переместительные законы, действия с числами 0 и 1), выполнять вычисления в 2–3 действия (без скобок), решать задачи на все арифметические действия, составлять взаимообратные задачи.
Личностные УУД: мотивируют свои действия; выражают готовность в любой ситуации поступить в соответствии с правилами поведения; испытывают желание оказания помощи в обучении товарища.
Метапредметные (критерии сформированности / оценки компонентов универсальных учебных действий – УУД): регулятивные: контролируют свои действия по точному и оперативному ориентированию в учебнике; оценивают результат своей деятельности; познавательные: выполняют учебные задачи, не имеющие однозначного решения; приводят примеры в качестве доказательства выдвигаемых положений; коммуникативные: доносят свою позицию до всех участников образовательного процесса; слушают и понимают речь других (одноклассников, учителя); решают поставленную задачу.
Ход урока
I. Устный счет.
1. Найдите «лишнее» число в каждой строке:
3 6 12 14 24 48
49 42 35 27 28 21
10 20 25 30 40 50
2. Разгадайте правило, по которому составлены схемы, и вставьте числа в «окошки»:
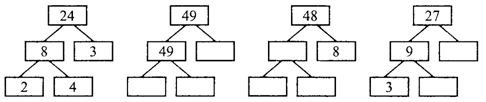

3. Сравните (>, < или = ?).
8 · (4 · 6) ... (8 · 4) · 5 9 · 3 · 2 ... 9 · 6
2 · (3 · 9) ... 6 · 9 6 · 8 · 4 ... 48 · 3
4. Игра «Математические горки».
– Какая сумма больше – слева или справа?
| 1 21 321 4321 54321 654321 7654321 87654321 987654321 | 9 89 789 6789 56789 456789 3456789 23456789 123456789 |
II. Сообщение темы урока.
– Рассмотрите схемы на доске:

– Что они изображают?
– Сегодня на уроке будем выполнять сложение и умножение с числами 1 и 0.
III. Работа по учебнику.
– Прочитайте задачу 1. Что известно? Что требуется узнать? Выполните краткую запись и решите задачу.
1-й приятель – 15 значков;
2-й приятель – 27 значков;
3-й приятель – ? значков.
Всего – 42 значка.
Решение:
1) 15 + 27 = 42 (зн.) – принесли 1-й и 2-й приятели;
2) 42 – 42 = 0 (зн.) – принес 3-й приятель.
Задание 2. Какова площадь прямоугольника? (6 кв. см.)
– Запишите равенство. 1 · 6 = 6 (кв. см).
Задание 3. Число 0 играет особую роль при сложении, а число 1 – при умножении чисел.
Справочный материал для учителя.
Цифра 0.
– Сегодня мы познакомимся с цифрой 0. Это самая загадочная и необычная цифра, которой обозначают «отсутствие» чего-либо. Прибавьте 0 к 5 – получится 5. Ведь мы ничего к числу не прибавили – вот оно и осталось без изменения. Отнимите 0 от 6 – получится опять-таки 6. Сосчитайте, сколько в нашем классе сковородок. (Ни одной, значит, 0.)
Казалось бы, что о нем говорить: 0, он и есть 0, пустышка. Недаром никчемного человека называют «ноль без палочки». Значит, подумает кто-то, ноль вовсе пустяковая цифра, без которой легко обойтись. Но это не так. Если разобраться, то выйдет, что 0 – очень даже важная «персона». Как, например, написать число 10, если нет 0? Долгие века люди не находили ответа на вопрос, как сделать так, чтобы запись цифр была простой и понятной. И 0 помог в решении этой проблемы.
– Вычислите суммы и произведения.
10 + 0 = 10 0 + 12 = 12 10 · 1 = 10 1 · 12 = 12
111 + 0 = 111 0 + 0 = 0 111 · 1 = 111 1 · 1 = 1
– Сформулируйте правило прибавления числа 0. (Если к числу прибавить 0, то это число не изменится.)
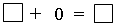
– Сформулируйте правило умножения на 1. (Если число умножить на 1, то это число не изменится.)
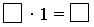
Задание 4. Посчитайте по цепочке.
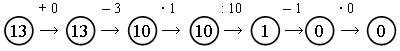
Задание 5. Что будет, если прибавлять 1? (Получим следующее число.) Какое получится число, если к числу 99 прибавить 1? (100.) А к числу 100? (101.) А к числу 123? (124.)
– Сформулируйте общее правило: какое число получается при прибавлении к числу единицы?
Задание 6. Запишите с помощью умножения сумму пяти нулей. 0 + + 0 + 0 + 0 + 0 = 0 · 5 = 0
– Найдите произведение 5 · 0.
– Сформулируйте правило умножения числа на 0. (Если умножить число на 0, то получится 0.)
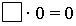
Задание 7. Расставьте в клеточках числа 0 и 1.
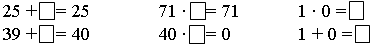
Задание 8 (работа в парах). Заполните свободные клеточки.
1 · 1 = 1 0 + 0 = 0 1 · 0 = 0
1 + 0 = 1 1 · 1 = 1 1 + 1 = 2
Задание 9. Выполните действия.
22 + 34 = 56 23 + 34 = 57 46 – 12 = 34 47 – 11 = 36
22 + 33 = 55 23 + 33 = 56 46 – 11 = 35 47 – 12 = 35
– Сравните выражения каждого столбика.
– Объясните результаты, обращая внимание на чётность чисел.
• Чётное число плюс чётное – получается чётное число.
• Чётное число плюс нёчетное – получается нёчетное число.
• Чётное число минус чётное – получается чётное число.
• Чётное число минус нечётное – получается нечётное число.
Задание 10. Буква «ч» обозначает чётное число, а буква «н» – нечётное. Поставьте в пустые клетки нужные буквы.
н + ч = н н + н = ч ч – н = н н – н = ч
ч + н = н ч + ч = ч н – ч = н ч – ч = ч
– Придумайте числа для каждого равенства. Проверьте свой ответ.
7 + 8 = 15 7 + 7 = 14 16 – 3 = 13 17 – 3 = 14
8 + 7 = 15 8 + 8 = 16 13 – 2 = 11 14 – 2 = 12
– Придумайте и нарисуйте картинки к равенствам.
IV. Фронтальная работа.
– Вы знаете, что числа бывают чётные и нечётные.
Чётными являются следующие, например, числа: 2; 4; 6; 8.
Нечётные числа – это 1; 3; 5; 7.
Четное число делится на 2.
– Его можно представить в виде суммы двух одинаковых слагаемых. Например, 26 = 2 × 13 = 13 + 13.
Дата: 2018-12-21, просмотров: 883.