Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Эти гипотезы также называют: гипотезы о сходимости распре­делений, выравнивание статистических распределений, подбор теоре­тического распределения.

а)  выравнивание статистического распределения с использованием  c²  - критерия (Пирсона)

Проверка гипотез о законах распределения основываются на изучении меры расхождения между статистическим и теоретический распределениями.

Предположим, что произведены наблюдения над некоторой слу­чайной величиной. Все полученные наблюдения разбиты на l интер­валов. В каждый интервал попало mi число наблюдений (рис.5.5).

f( t )

t

,  ,  , , , ,  , ,

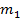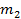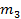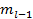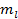1 2 3

Рис. 5.5. Интерпретация интервалов наблюдений по оси времени

 

при этом

m ₁ + m ₂ +· · · + m_l = n  (5.7)

где n - общее количество наблюдений (испытаний);

m_i- статистическое значение числа наблюдений (испытаний), попавших в i-й интервал

Обозначим  P_i  -  теоретическое значение вероятности попадания наблюдений в i интервал.  

Следовательно,

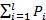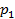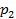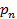 = + + · · · +  =1 ,   (5.8)

Умножив на n ,  получим

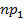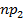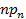+ + · · · +  = n ,           (5.9)

где 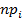 - теоретическое значение числа наблюдений (испытаний), попавших в i-й интервал.

При построении критерия c² в качестве меры расхождения между статистическим и теоретическим распределениями используется расхождение между теоретической и статистической частотами.

Рассмотрим некоторую случайную величину x i, равную

 

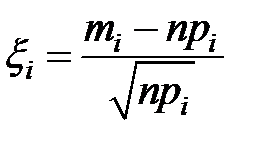                             (5.10)

       Величина xi распределена асимптотически нормально. Очевидно, распределение величины x i будет тем ближе к нормальному, чем будут больше величины 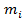и 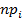 то есть, когда объем наблюдений будет достаточно велик.

       Обычно требуется, чтобы 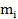= 8¸10

Рассмотрим распределение сунны величин x _i ² , то есть:

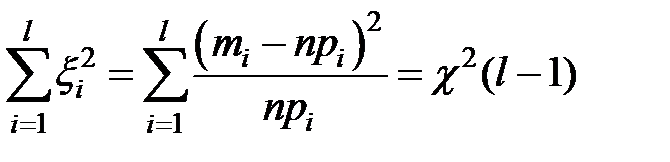
(5.11)

 

то есть величина 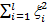подчиняется  c² - распределению с числом степеней свободы

 k = l - 1, где   l - количество интервалов.

Число степеней свободы k  уменьшают на единицу, так как  накладывается условие:

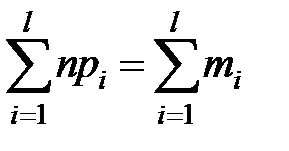                     5.12)

Кроме того необходимо учесть, что при подборе теоретического распределения eго параметры  вычисляются по данным статистических наблюдений (испытаний).  Чтобы уменьшать возникшую в связи с этим ошибку, количество степеней свободы c² -распределения уменьшают еще на число параметров предполагаемого закона распределения. Следовательно, при проверке гипотезы о законе распределения в этом случае используют c²   - распределение с k = l - c -1 степенями свободы,  где c- число параметров теоретического распределения.

Для проверки выдвинутой гипотеза поступают двояко:

а) сравнивают вычисленное значение критерия  c² , с его теоретическим значением 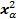( k ), взятого при уровне значимости a и числе  степеней свободы k = l - c -1

Если при этом окажется,  что c² £  ( k ), то принимается нулевая  гипотеза Н_о, если же c² £  ( k ),то гипотеза  Н_о  отвергается. Однако при этом нельзя утверждать, что гипотеза Н₁ справедлива;

 б) находят значение вероятности Р { c² £  ( k )}. Если эта вероятность велика, то принимают гипотезу  Н_о . Это значит,  что расхождение между частостями  m_i и 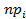 является неслучайным, а полученное статистическое распределение согласуется с предполагаемым теоретическим  распределением.

Чем больше объем наблюдений, тем при меньшем значении вероятности Р{ x² ³ 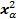 ( k )} можно принимать нулевую гипотезу Н_о.

 Считают, что при  n £  100  можно принимать Н_о Р ³ 0,2 ¸0,3. При больших  n значение  Р может быть взято меньше ( при n ³ 1000 ; Р ³ 0,05).

 Рассмотрим пример выравнивания статистического распределения, построенного по данным таблицы 5.1.

По данный   получено:

 

Таблица 5.1

Интервал	m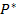i	(Ti)	Zi	j (Zi)	F(Zi)	pi	npi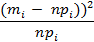
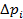
1	2	3	4	5	6	7	8	9	10
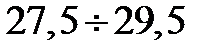
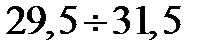
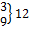
		0,071	-1,47	-0,4292	0,0708	0,0708	12	0	0,0002
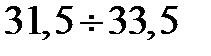
	23	0,135	-0,860	-0,3050	0,1950	0,1242	21,2	0,153	0,0108
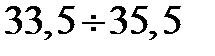
	33	0,194	-0,213	-0,0987	0,4013	0,2063	35,2	0,137	0,0123
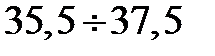
	33	0,224	0,353	0,1368	0,6368	0,2355	40,0	0,100	0,0115
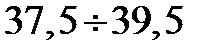
	34	0,200	0,960	0,3315	0,8315	0,1947	33,2	0,02	0,0053
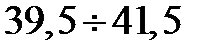
	21	0,124	1,565	0,4406	0,9406	0,1091	18,7	0,283	0,0149
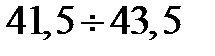
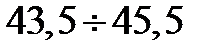
		0,053	2,780	0,4972	0,9972	0,0566	9,7	0,050	0,0036
Суммы	170	1,00					170	0,725	Суммы

 

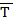_о  = 36,335; S ² ( T ) = 10, 37 ; s = 3,3 .

Значения величин (таблица 5.1) вычислялись по формулам:

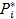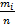 = ; _D Р _i = 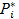- Р _i,    где n = 170.

Схема решения:         

Вычисляется Z_i = 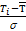по таблицам функции Лапласа определяется значение Ф( Z_i ) и  значение F ( Z_i ) =0,5 + Ф( Z_i ) ;

находится значение теоретической частоты  Р _i = F ( Z_i ) - F ( Z_{i - 1} ) и вычисляется значение n p_i = 170 P_i; 

       определяется величина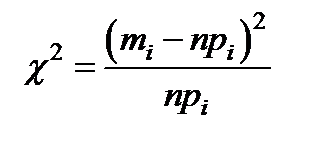

При вычислении значений pi в качестве теоретического распределения принято нормальное.

В формуле для вычислена Z_i  значение T_i берется равным значению Т для конца интервала, так например для первого интер­вала Т₁ = 31,5 и

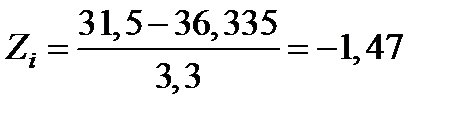
По результатам вычислений получено:

c ²= 0,725 (статистическое значение  c² - критерия).

Находим значение 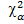 ( k )   при уровне значимости α =0,05 и числе степеней свободы K = l - с - 1 = 7 - 2 - 1 = 4, где l = 7 - число интервалов после объединения; с  = 2 - количество наложенных связей, равное количеству параметров забранного распределена (для нормального с = 2).       Находим:

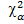 ( k )   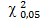=  (4)   = 9,49  (  по табл.. 9 приложения 2).

 

Так как x ² = 0,725 < 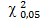 (4)   =9,49, то вычисленное значение критерия не попадает в критическую область, а гипотеза о выбранном законе распределения не отвергается.

В случае использования второго способа проверки гипотезы о сходимости статистического распределения с нормальным распределением по таблицам x² -распределения определяемся значение вероятности 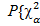 ( k )   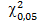=  (4)}   

Если эта вероятность достаточно велика, это расхождение между статистический и теоретическим распределениями случайно (незначимо ) и, следовательно, нулевая гипотеза должна быть принята.

В нашем случае 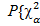 ( k )   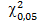=  (4)}  = 0,94,

т.е. расхождение между статистическим и теоретическим распреде­лениями случайно с вероятность 0,94.

Если бы эта вероятность была мала, то это означало бы, что расхождение между - теоретическим а статистические распределениями не случайно, и нулевая гипотеза должна быть отвергнута.

Некоторые замечания о  критерии c ² . Он является достаточно мощным критерием, однако ему присущи определенные недостатки:

а) в некоторых интервалах количество наблюдений мало, их приходится объединять с соседними интервалами, что может привести определенной погрешности;

б) параметры теоретического распределения находятся по статистическим данным. И хотя это учитывается уменьшением числа степеней свободы, но не гарантирует от ошибок;

в) учитывая ( a ) и принимая во внимание, что для ряда законов необходимо иметь l ≥ 4 , чтобы K= l - c -1 ≥ 1, т.е., этот критерии можно применять при числе наблюдений n ≥ 30 (чтобы в каждом интервале было не менее 8 наблюдений).

 

5.3. Выравнивание статистического распределения   с использованием  λ - критерия  (критерия Колмогорова)

В 1933 году Гливенко и Колмогоров показали,  что если F(x)  функция распределения случайной величины ( x º t )   является непрерывной, то величина  D_n  рав­ная максимальной разности теоретического и статистического значе­ний этой функции, умноженная на 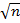 , т.е.

D_n = max | 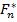(x) - F(x)|  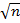           (5.13)

имеет своим пределом распределение, вычисляемое по формуле:

P{D_n£l} = 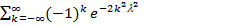(5.14)

и независимо от вида функции F(x)

       Здесь: 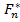(x)- статистическая функция распределения случай­ной величины ( x º t )  , определяемая по объему наблюдений n;

       F(x) - теоретическая функция распределения случайной величины ( x º t )   ;

       n - число наблюдений (испытаний).

       Критерий Колмогорова использует  в качестве меры расхождения  максимальную разность между F(x) и 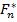(x)  ( см. рис. 5.6) .

F(x)

F(x)

x

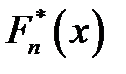
Dn

Рис. 5.6. Графическая интерпретация меры расхождения  между F(x) и 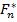  (x)

       Если имеется достаточно большое количество наблюдений n, то при всяком λ > 0 вероятность того, что D_n  ≤  λ, обоз­начаемая через K(λ), равна;

P{D_n < l}= k(l) = 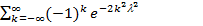(5.15)

Тогда

       P{D_n > l}=1- k(l) = 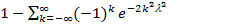(5.16)

Следовательно, если вероятность  P { D_n > l } -достаточно велика, то расхождение между 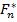(x) и F ( x ) будет случайным . В противном случае, если вероятность эта мала, то расхождение будет неслучайным и гипотеза о сходимости распределений должна быть отвергнута

Схема решения задача с помощью λ - критерия;

а) По экспериментальным данный строится статистическая функция распределения 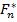(x) и сравнивается с предполагаемые теоретическим распределением F(x);

б) Определяется максимальная разность между этими функциями, max | 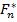(x) - F ( x )|;

в) Вычисляется значение критерия λ_о ,

 λ_о = max | 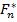(x) - F ( x )| ;       

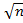г) По значению λ_о определяется вероятность P{D_n > l _о} с использованием таблиц λ - критерия (табл. 12 приложения 2).

Если эта вероятность велика, то расхождение случайно и нулевая гипотеза принимается.

Пример.

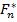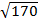n = 170;     max | (x) - F ( x )|   = 0,0149;       l _о =0,0149 =0,194

По таблицам  для λ - критерия, находим:

P{D_n > 0,194}= 1- k(0,194) = 1 , следовательно, гипотеза о нормальном распределении принимается.

Критерий Колмогорова всегда дает завышенное значение сходимости распределений.

Оценка  λ  критерия:

a) Метод проверки гипотезы очень прост. т.к. оценивается расхождение только в одной точке;

б) Не учитывается факт, что параметры предполагаемого теоре­тического распределения вычисляются по статистическим данным, поэтому, как правило, получаются завышенные результаты сходимости;

в) λ - критерий необходимо применять в случае, если известны параметры теоретического распределения (что практически редко имеет место);

г) Обычно применяется при малом объеме наблюдений, когда точность принятия решений мала, а задача решается упрощенно.

Чем меньше n , тем выше надо устанавливать критическую границу вероятности сходимости (при n = 10 ¸15 - нулевая ги­потеза принимается при P{D_n > l _о}³0,05; при n ≥ 100  значение P ≥ 0,01 ¸ 0,05, но при таком числе наблюдений лучше пользоваться критерием   x ².