Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Наиболее часто приходится проверять следующие вида гипотез:

- гипотезы об однородности средних выборочной и генеральной совокупностей;

- гипотеза об однородности средних двух выборочных совокупностей (т.е. проверку их принадлежности к одной и той же гeнеральной совокупности);

- гипотезы об однородности средних нескольких (более двух) выборочных совокупностей.

При проверке однородности средних полагаем, что выборки взяты из нормального распределенных генеральных совокупностей .

a) Проверка однородности средних выборочной и генеральной совокупностей.

Рассмотрим два случая:

1) Когда дисперсия D( x ) генеральной совокупности известна.

В этом случае подданным статистических наблюдений вычис­ляется V - статистика , значение которой сравнивается со значением величины 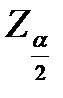 или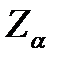

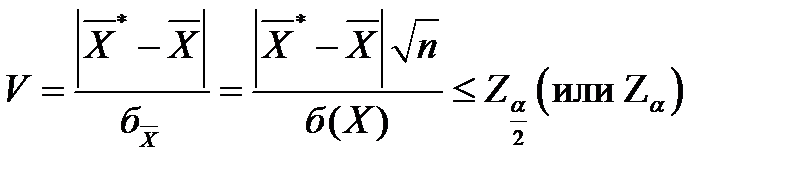                                           (5.28)

где   =  ,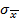

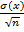n - объем наблюдений;

2) Когда дисперсия генеральной совокупности неизвестна. В этом случае значение V - статистики сравнивается с значением величин: Z или t.

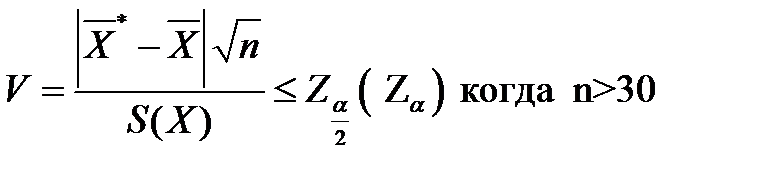                                               (5.29)

или

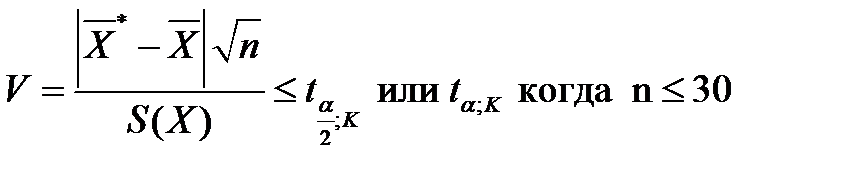                                      (5.30)

где S( x ) - среднее квадратическое отклонение величины  x  в выборке объемом  n ;

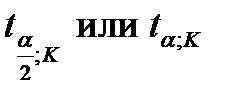- значение t -критерия, взятого при уровне значимости α/2 (или α) b числе степеней свободы К=n-1 .

Пример:

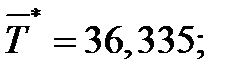
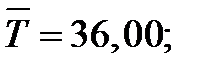
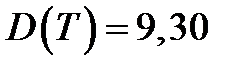 т.е.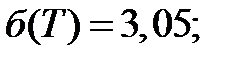    

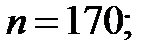
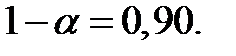
Вычисляем значение Ѵ -статистики:

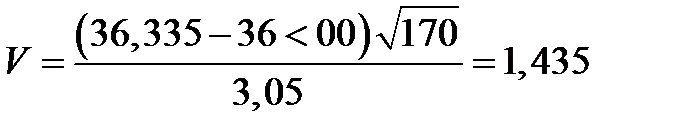
Пользуемся двухсторонним критериев, тогда 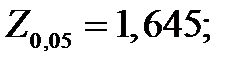( приложение 2 табл. 3)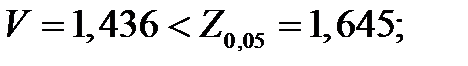

Следовательно, расхождение между средними значениям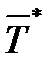и  и 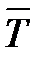 случайно (незначимо), и гипотеза об однородности этих величин должна быть принята.

Если D(T) – неизвестна, а S(T) =3,3, то будем иметь:

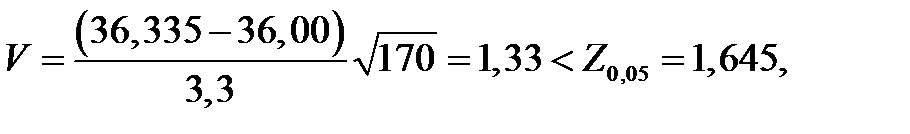
гипотеза о равенстве средних , с вероятностью 0,95 не отвергается;

б) Проверка гипотезы о равенстве двух выборочных средних.

1) Дисперсия D( x ) генеральной совокупности известна.

Проверка производятся с использованием  V - статистики, т.е.

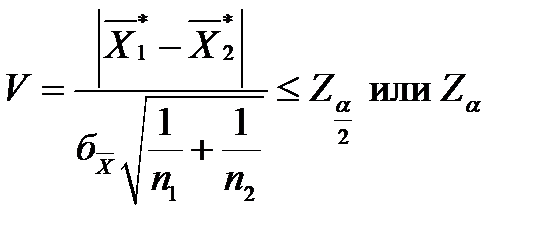                      (5.31)

2) Дисперсия генеральной совокупности неизвестна. В этом случае значение. V - статистики вычисляется по формуле:

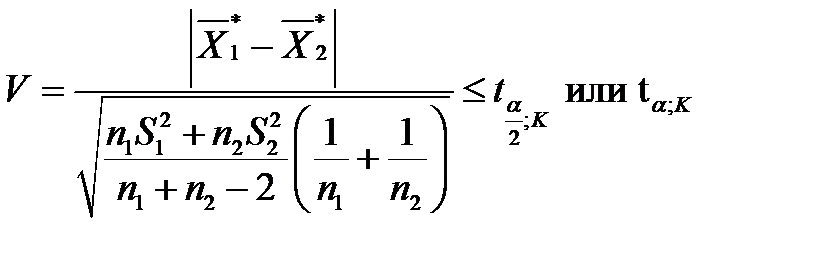                                         (5.32)

где 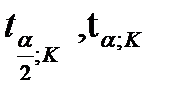 - значение t -критерия, взятого при уровне значимости α/2 и α и числе степеней свободы ;

 

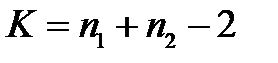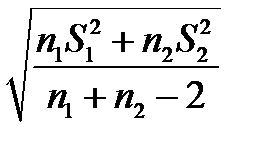 - приведенная дисперсия.

Пример

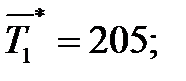
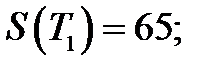
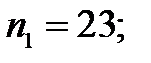
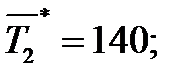
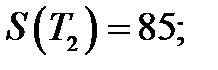
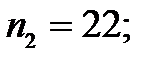
Ранее для этого прамера проверялась однородность дисперсий . Проверим однородность средних по  значению V -статистики :

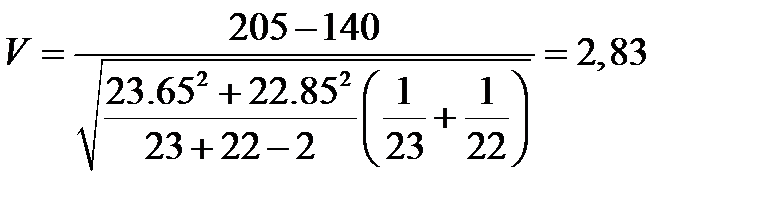
Зададимся доверительной вероятностью 1 - α = 0,90. Тогда для α/2 = 0,05 и К= 23+22-2=43:

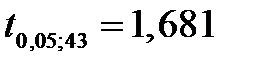; т.е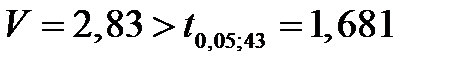

Следовательно, гипотеза о случайности расхождений средних этих групп наблюдений должна быть отвергнута;

3)  Дисперсия выборочных совокупностей неоднородны.

В этих случаях используется приближенная зависимость:

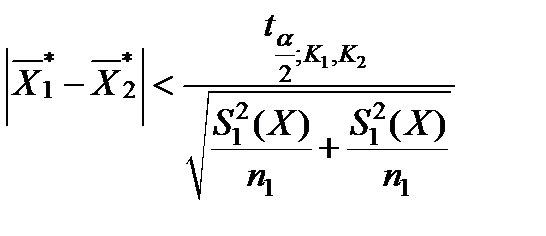 (5.33)

Величина 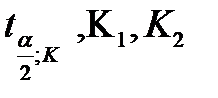 представляет собой приведенное значение  t - критерия и вычисляется по формуле:

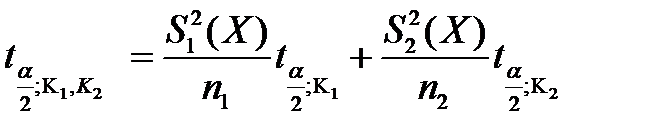                                                        (5.34)

Пример.

   

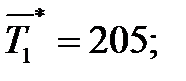
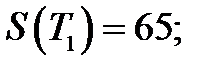
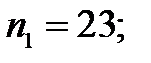
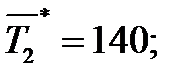
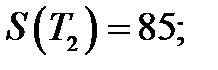
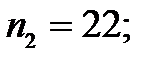
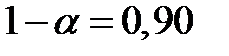
Проверим однородность дисперсий с использованием F - критерия

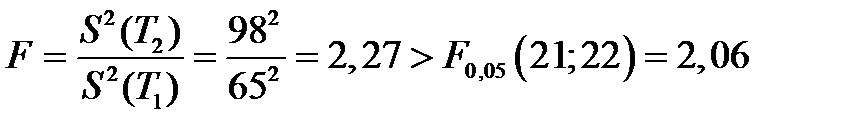
т.е. расхождение дисперсай не случайно.

Проверяем однородность средних, т.е. устанавливаем справедливость неравенства

,

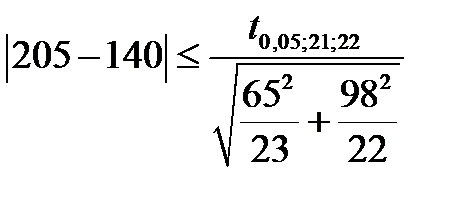где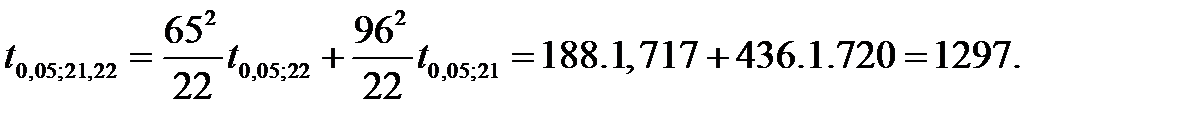

В связи с тем, что 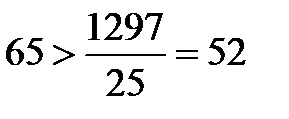, то гипотеза о случайности расхождений между средними должна быть отвергнута.

в) Проверка гипотез об однородности средних нескольких выборочных совокупностей , т.е. когда их число более двух.

Рассмотрим два случая:

1) с использованием F - критерия

В этом случае статистическое значение F -критерия вычисляется по формуле:

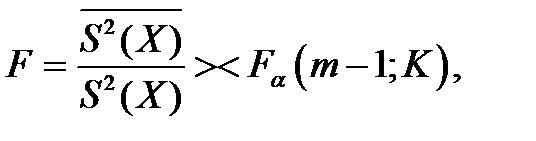                                                                    (5.35)

где

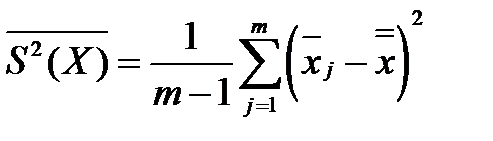- дисперсия, характери­зующая рассеивание средних значений;

m    - число сравниваемых средних;

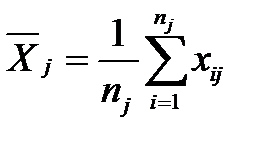 - среднее значение случайной величины в j -той выборке;

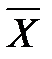 - Среднее значение m - средних величин:

если 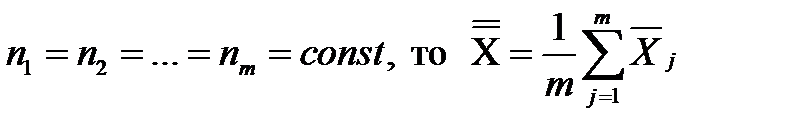 если объемы наблюдений различны, то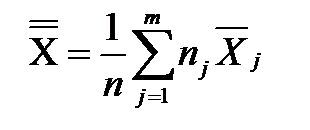

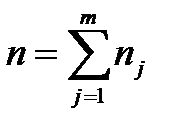 - общее число наблюдений ;

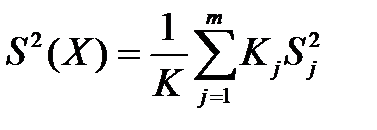 - оценка дисперсий 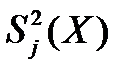(средневзвешенная дисперсия);

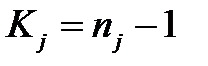- число степеней свободы j -той выборки;

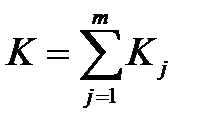 - общее число степеней свободы.

Таким образом, F - статистика в этом случае представляет собой отношение двух дисперсий, из которых одна характеризует рассеивание средних, а другая представляет собой средневзвешенное значений всех дисперсий. Здесь всегда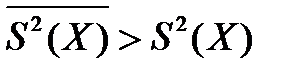

Вычисленное значение F - статистики сравнивается с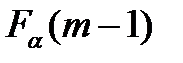

Пример.

Проверим однородность средних для условий, приведенных в  таблице 5.1 и K= 27; m = 5 ; n = 32; α = 0,05.

Вычисляем рассеивание средних величин

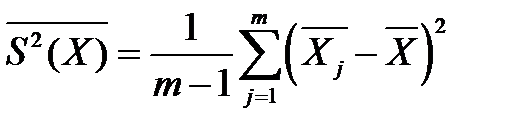
Где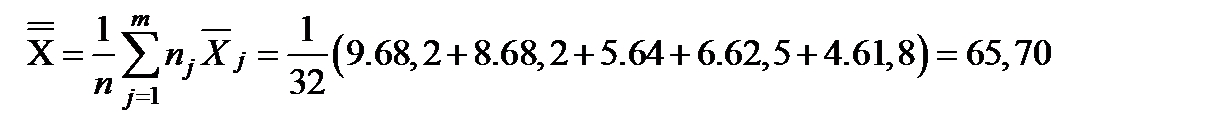

Тогда: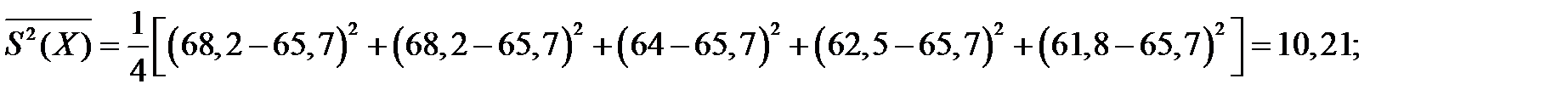

 

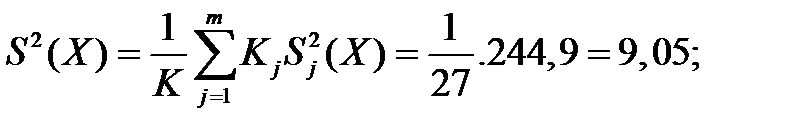
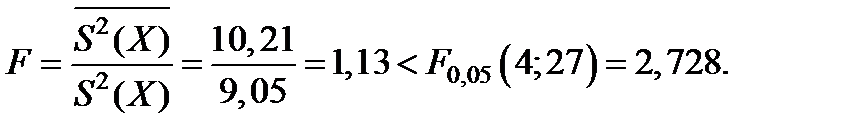
Следовательно, расхождение между средними величинами незна­чительно, т.е. толщина стенки трубы  несущественно влияет на величину харак­теристики прочности б_в;

2)   Использованием  L_о - критерия.

Здесь L_о - преобразованный критерии Неймана - Пирсона .

Статистическое значение величина L_о  вычисляется по формула:

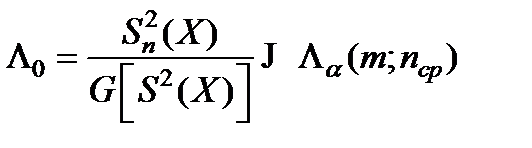,    (5.36)

где 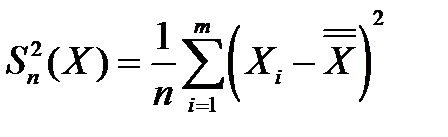 - полная дисперсия выборочных значений;

 - общее число наблюдений;

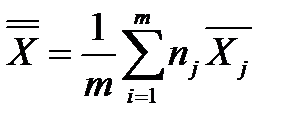- общая средняя /среднее значение средних ве­личин;

m - число групп наблюдений;

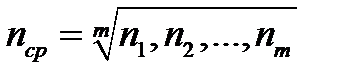 - среднее геометрическое значение числа наблюдений (приведенное число наблюдений);

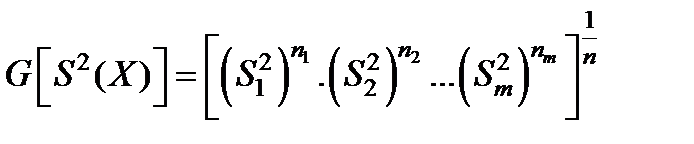- средняя геометрическая дисперсия выборок.

Необходимо иметь в виду, что проверка однородности средних должна предшествовать проверке однородности дисперсий.

Пример . Дано m = 5; α = 0,05

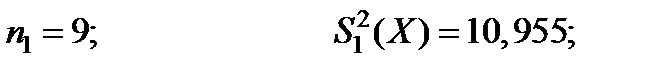
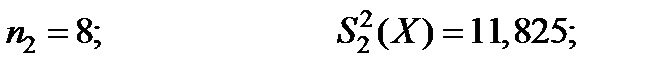
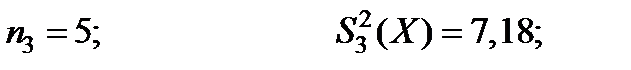
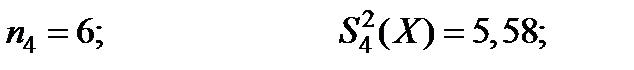
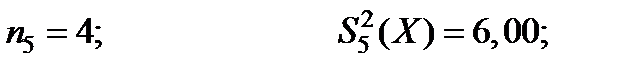
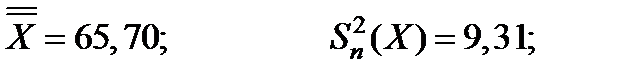
Вычисляем значение величин, входных в формулу (5.36):

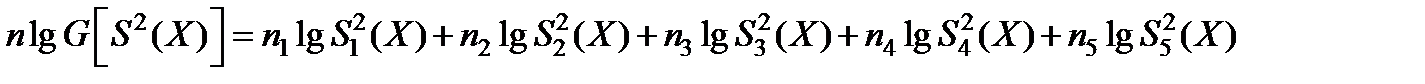
Или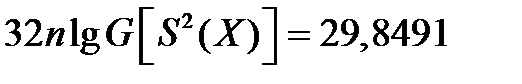

Откуда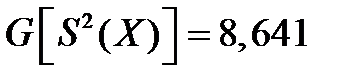

Тогда статистическое значение; /'о -критерия, ;

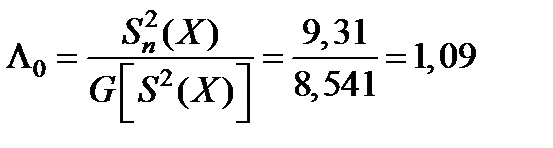
Приведенное значение числа наблюдений •

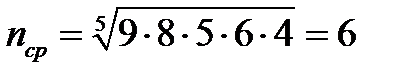
По таблице 15, для 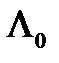 -критерия, определяем:

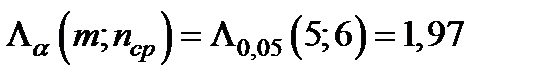
Так как 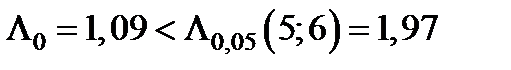 то выборочные характе­ристики однородны и, влияние толщины стенки  на   s _в   незначимо . При этом полагаем, что выборочные наблюдения взяты из генеральной совокупности, распределенной по нормальному закону. Применение t -критерия допустимо и для проверки гипотезы об однородности выборочных, наблюдений, относящихся к генеральной совокупности, у которой распределение несколько отличается от нормального.

Если распределение признака генеральной совокупности не подчиняется нормальному распределению, то в таких случаях для проверки гипотез об однородности наблюдений применяются непараметрические гипотезы и критерии.