Проверка однородности (равенства) дисперсий означает проверку случайности расхождения сравниваемых характеристик.
a) Проверка однородности дисперсий выборочной и генеральной совокупности
Для решения этой задача может быть использован c2 -критерий или F критерий.
Проверка гипотез с использованием c2 - критерия. Для этой цели используются неравенство следующего вида:
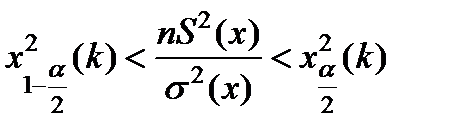 (5.19)
(5.19)
когда используется двухсторонний критерий;
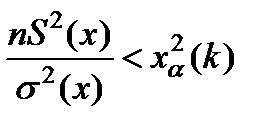 (5.20)
(5.20)
когда используется односторонний критерий.
Здесь обозначено: n - число наблюдений;
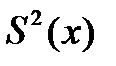 - статистическая дисперсия случайной величины x ;
- статистическая дисперсия случайной величины x ;
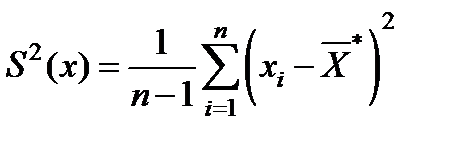
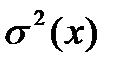 - дисперсии генеральной совокупности ;
- дисперсии генеральной совокупности ;
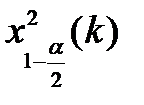 и
и 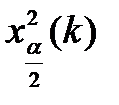 квантили случайной величины
квантили случайной величины 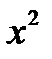 , взятые при уровнях значимости 1-α/2 и α/2 и числе степеней свободы k=n-1.
, взятые при уровнях значимости 1-α/2 и α/2 и числе степеней свободы k=n-1.
Рассмотрим следующий пример .
Проверить однородность статистической дисперсия и дисперсии генеральной совокупности , если известно:
n = 170; S2(T) = 10,87; б2(T) = 9,20; α = 0,10 .
По таблицам c2 - распределения определяем:

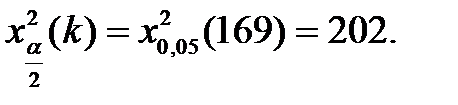
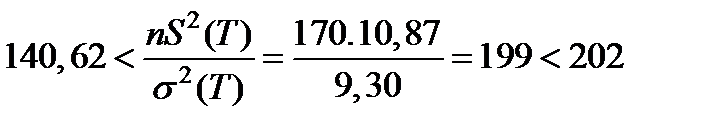
Следовательно, сравниваемые дисперсии S2(T) и s 2 (T) однородны, тo есть расхождение между ними случайно.
В случае использования одностороннего критерия, имеем:
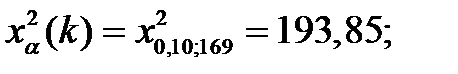
то есть 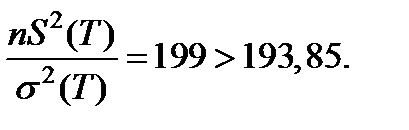
Следовательно, с уровнен значимости α = 0,10 гипотеза о случайном расхождении дисперсий S2(T) и s 2 (T) должна быть отвергнута.
Проверка гипотез с использованием F - критерия. В этой случае используется зависимость:
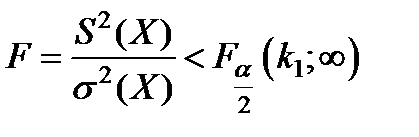 (5.21)
(5.21)
Когда применяется двухсторонний критерии;
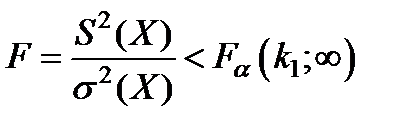 (5.22)
(5.22)
когда применяется односторонний критерия.
При использовании формул (6.5) и (6.4) в числителе должна стоять большая дисперсия.
Если окажется, что s 2 (T) > S2(T) , то формулы (6.3) и (6.4) принимает вид:
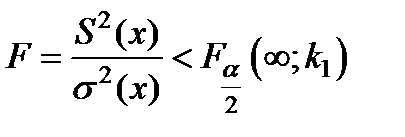
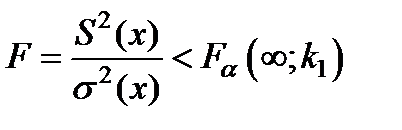
В приведенных формулах 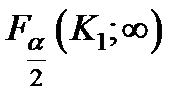 и
и 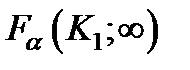 значения c2 - критерия взятые при уровнях значимости α/2 и α числе степеней свободы числителя k 1 = n - 1 и знаменателя ∞.
значения c2 - критерия взятые при уровнях значимости α/2 и α числе степеней свободы числителя k 1 = n - 1 и знаменателя ∞.
Рассмотрим пример применения формул.
Дано: n = 170; 1 - α =0,90; S 2 ( T ) = 10,87; 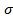 2(Т) = 9,3
2(Т) = 9,3
Вычисляем значения F - критерия
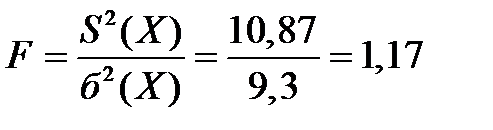
Табличное значение F - критерия для 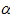 = 0,05; К1=169 и К2= ∞ (таблица 10):
= 0,05; К1=169 и К2= ∞ (таблица 10): 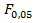 (169;
(169; 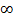 ) = 1,29
) = 1,29
Поскольку F = 1,17 < 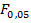 (169;
(169; 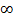 ) =1,22
) =1,22
то при использовании двухстороннего критерия гипотеза о случайности расхождений между б2(Т) и S2(T) не отвергается .
В случае использования одностороннего критерия F = 1,29 > 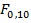 (169;
(169; 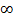 ) =1,14 . Следовательно, и этом случае гипотезе о случайности расхождений дисперсий отвергается.
) =1,14 . Следовательно, и этом случае гипотезе о случайности расхождений дисперсий отвергается.
Если статистическое значение критерия близко к его теоретическому значению, то нужно. проверять гипотезу с использованием как c2 -критерия, тек и F - критерия.
б/ Проверка однородности дисперсий выборочных совокупностей
Проверка однородности дисперсий двух выборочных совокупностей. Обычно эта проверка осуществляется с использованием F- критерия:
F = 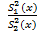 ³
³ 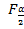 ( K 1; K 2 ) - - в случае двухстороннего критерия; (5.23)
( K 1; K 2 ) - - в случае двухстороннего критерия; (5.23)
F = 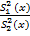 ³
³ 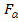 ( K 1; K 2 ) - в случае одностороннего критерия. (5.24)
( K 1; K 2 ) - в случае одностороннего критерия. (5.24)
В числителе, как уже указывалось, должна находиться большая дисперсия. Если же
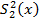 ³
³ 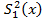 , то F =
, то F = 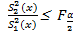 (K1;K2), F =
(K1;K2), F = 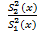 £
£ 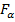 (K1;K2).
(K1;K2).
Пример : .
Проведено наблюдение над двумя группами насосных агрегатов, при этом n1 = 23 и n2 = 22 , для которых получены следующие значения наработок отказ:
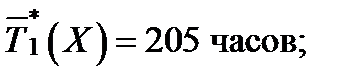
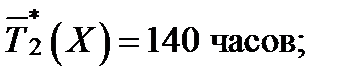
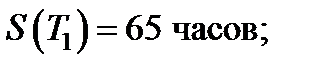
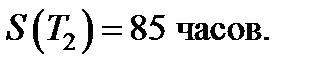
Проверить однородность дисперсий выборочных совокупностей при доверительной вероятности 1 - 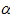 = 0,90.
= 0,90.
По таблице 10 при 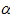 /2 = 0,05; К1 = 21 и К2 = 22, находим:
/2 = 0,05; К1 = 21 и К2 = 22, находим:
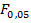 (21; 22) = 2,06
(21; 22) = 2,06
Вычисляем дисперсионное отношение и сравниваем его с табличным:
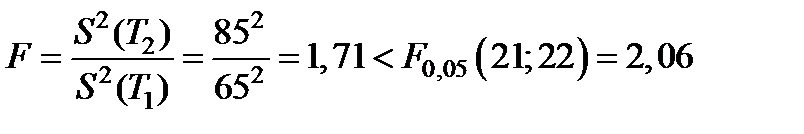
Следовательно, гипотеза о случайности расхождений между дисперсиями должна быть принята (при такой разнице в дисперсиях это объясняется малым числом наблюдений (испытаний) n1 и n2).
Проверка гипотезы об однородности дисперсий, когда число групп наблюдений более двух. Для этой дела могут быть использованы два вида критериев:
G - критерий (критерий Кочрена), когда объем наблюдений в группах одинаковы, т.е. n1 = n2 = ... = nm.
Значение G -критерия выделяется по следующей формуле:
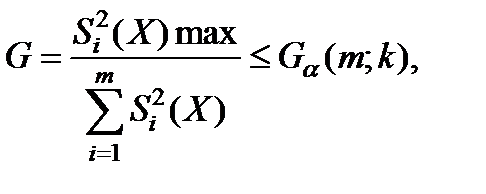 (5.25)
(5.25)
где α - уровень значимости;
m - число групп наблюдена;
k = n-1 - число степеней свободы,
Пример.
Была проанализирована статистическая информации по 4 насосным станциям о времени восстановления насосных агрегатов, m=4. Объем выборки в каждой группе статистической информации составил n =17; при этом:
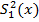 = 40;
= 40; 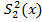 = 30 ;
= 30 ; 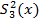 = 50;
= 50; 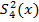 =20.
=20.
Проверить однородность дисперсий при α = 0,05 (таблица 13 для G - критерия составлены для α = 0,05 и α = 0,01).
В рассматриваемом случае 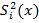 max =
max = 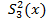 .
.
G= 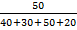 =
= 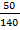 =0.357 < G0,05 (4; 16) = 0,4366
=0.357 < G0,05 (4; 16) = 0,4366
Следовательно, гипотеза о случайности расхождения между m дисперсиями не отвергается.
Как видим, проверка с помощью G - критерия очень проста, но критерий не очень чувствителен .
М - критерий (критерий Бартлетта) - используется для проверки однородности дисперсий, когда объемы наблюдений в каждой группе различны. Значение М - статистики вычисляется по следующей формуле :
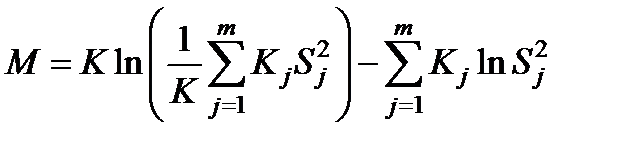 (5.26)
(5.26)
где 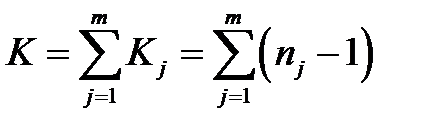 - с суммарное число степеней своды;
- с суммарное число степеней своды;
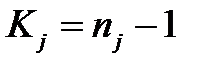 - число степеней свободы в j -той группе наблюдений:
- число степеней свободы в j -той группе наблюдений:
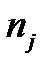 - число наблюдений j -той группе;
- число наблюдений j -той группе;
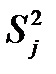 -дисперсия в j - той группе наблюдений.
-дисперсия в j - той группе наблюдений.
Вычисленное значение М -критерия. сравнивается с величинами ma(α;m;c) и mb(α;m;c)
Здесь С1 вычисляется по формуле:
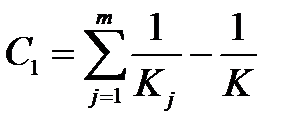 (5.27)
(5.27)
Если вычисленное значение М - критерия меньше ma(α;m;C1) для всех значений С1 , то принимается гипотеза об однородности дисперсии.
Если 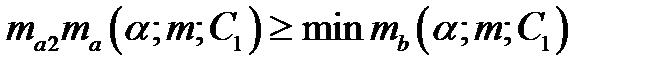 , то вычисляется значение С1 .
, то вычисляется значение С1 .
Для вычисленного значения С1 и значений α и m по таблицам определяются величины ma и mb .
Если ma(α;m;c1) ≤ M то гипотеза отвергается, если M < mв(α;m;С1), то гипотеза принимается.
При проверке однородности дисперсий следует отдавать предпочтение критерию Бартлетта, т.к. он более мощный, чем G - критерий.
Если G -критерий дает отрицательный ответ об однородности дисперсий, то необходимо проверить гипотезу с использованием M - критерия.
Пример.
Проведено исследование характеристики прочности стальных труб с толщиной стенки d. Результаты исследований приведены в таблице 5.1.
Таблица 5.1
| d j - толщина стенки, мм | 1 | 2 | 3 | 4 | 5 |
| nj - объем наблюдений | 9 | 8 | 5 | 6 | 4 |
| sвj - , кг/ мм2 | 68,2 | 68,2 | 64 | 62,5 | 61,8 |
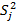 ( ( 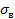 ) )
| 10,95 | 11,82 | 7,18 | 5.58 | 6 |
Однородность дисперсий S j ( s в ) при уровне значимости α = 0,05 проверяется по М -критерию.
Вычисляются значения величин, входящих в формулу для М - критерия
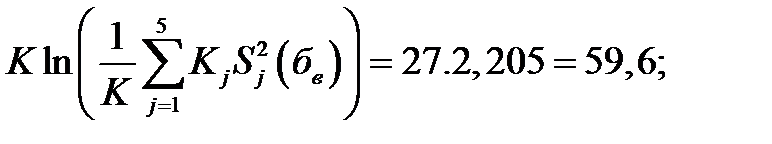
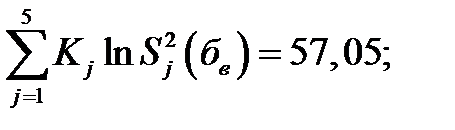
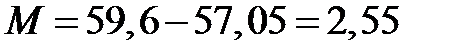
По таблицам для М - критерия, (приложение 2 табл. 14) находим : ma(α;m;c1) и mв(α;m;c1)
В этих таблицах С1 меняется от 0 до 5 .
При C1 = 0 ma = mв = 9,49,
C1 = 5 ma = mв = 11,02,
т.е. для всех значений С1 вычисленное значение М -критерия
М = 2,55 < mв =0,49 ¸ 11,02,
Дата: 2018-12-21, просмотров: 389.