При обработке статистических данных бывают случаи, когда отдельные наблюдения резко выделяются от результатов остальных наблюдений. Возникают сомнения о необходимости объединения всех этих данных при определении статистического закона распределения. В целях проверки сомнений выполняется проверка,  т.е.  уточняется условие по однородности выборки наблюдений.  

Для проверки однородности наблюдений используются несколько методов, но наиболее часто применяется следующий .

Первый вариант. Когда известны параметры теоретического закона распределения случайной величины.

Рассматриваемые ниже методы справедливы для случая, когда распределения выборочной и генеральной совокупности являются нормальными. С параметрами a и s ².

Результаты наблюдений располагаются в виде вариационного ряда, следовательно могут выделиться только крайние члены (первый или последний). Эти выделяющие члены называется экстремальными .

Проверка гипотезы об однородности наблюдений в этой случае заключается в проверке неравенства:

| x_э - x | £  t_{p , n}; s(x)           (5.17)

где t_{p , n} - размах  распределения этой разности при процентном пределе (вероятности) Р  и числе наблюдений  n.

Для величины t_{p , n} составлены специальные таблицы (таблице 11). Если неравенство соблюдается, то экстремальная  величина  вариа­ционного ряде является однородный в данной выборочной совокупнос­ти, и его отбрасывать не следует.

Если | x_э - x | > t_{p , n}; s(x) , то величина  x_э  - не принадлежит данной совокупности и должен быть исключен.

Пример.

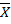 = x =  36,335;   s(x) = 3,3;   n = 170.

В вариационном ряду наблюдений имеется член x_э = 51, который резко отличается от других наблюдений. Принадлежит ли x_э  данному ряду?

Решаем задачу при a = 0,10, т.е. доверительная вероят­ность равна 1- a =Р =0,90,

По таблицах для t_{p , n}, находим: t _0,9;170 = 3, 2 (табл. II).  |51 - 36,335|   = 14,665 > 3,2  . Следовательно, величина x_э = 51 должна быть исключена из наб­людений при обработке статистических данных.

Но, как правило, параметров теоретического распределения мы не знаем, и чаще используется второй случай.

Второй вариант. Когда параметры закона распределения неиз­вестны.

Вводим допущение, что размах отклонения величины x_i  имеет нормальный закон распределения.  Определяем по статистические данным величины :

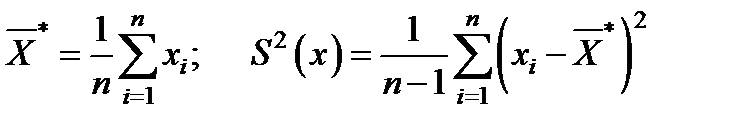
Вычисляем значение r (иногда ее называют "размахом") по следующей зависимости :

r = 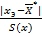       (5.18)

и сравниваем с значением этого критерия при уровне значимости a , (P = 1- a)  и числе наблюдений n.

Если 

r = 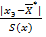 £ t_{p ; n}

то член принадлежит к рассматриваемому ряду.

Если равенство не соблюдается, то величина  x_э  из выборки данных должен быть исключен.

Пример:

n=8; 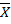^* = 62;      S ( x )= s = 2,4 x_э = 58,6; a= 0,І0; P=0,9 .

Определяем значение r .

r = 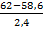=1,415

 По таблице ІІ определяем значение t_{p , n =}         = 2,2.

Сопоставляем значения  r и  t_{p , n ,} 1,415 < 2,2

 Следовательно, величина x_э при обработке результатов наблюдений не должен исключаться.