Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

       На практике соединение элементов в системе (в смысле надеж­ности) чаще всего приводится к комбинации последовательных и параллельных соединений. В этом случае, применяя многократно формулы (3.43) и (3.4.10) нетрудно рассчитать надежность системы. По­кажем это на примере (см. рис. 3.4 - 3.5).

Рис. 3.4 . Схема итераций преобразования сооружений объекта в модель надежности системы

       Рассчитывая  надежность каждой из обведенных пунктиром групп, мы считаем каждую из этих групп одним элементом с известной надежностью и получаем новую систему:

 

 

Рис. 3.5. Схема итераций по упрощению модели надежности объекта         

       Проделывая с этой системой ту же операцию, получаем третью систему и так далее до тех пор, пока не получим один элемент.  

Метод путей и сечений.

       Это один  из общих методов расчета надежности. Система из множества  элементов 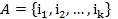рассматривается как путь:

       а)    Система исправна, если исправны все элементы этого множества независимо от состояния других элементов;

       б)    Никакое подмножество  А  не обладает свойством   (а).

       Пусть 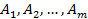- множество всех путей. Собы­тие, состоящее в том, что все элементы  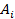исправны,  обозначим аналогично буквой 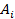.Тогда   функция надежности системы будет равна :

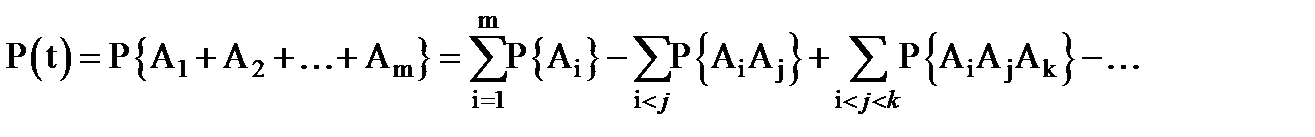(3.46)

       Каждая из вероятностей, стоящих в правой части,  вы­числяется по формуле ,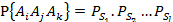

       где 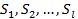- номера элементов, образующих пути  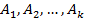(эти пути могут,   пересекаться). При небольшом числе путей m формула  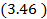удобна, при большом числе путей она неэффективна, так как число слагаемых правой части равно 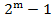. Существует прием, позволяющий в некоторых случаях уменьшать объем вычислений. Прежде всего , очевидно, что

,

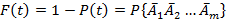       где 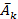- событие, дополнительное к 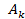. Два пути на­зовем пересекающимися, если они имеют хотя бы один общий эле­мент. Два пути назовем связанными, если их можно соединить це­почкой пересекающихся путей. Поскольку понятие связанности яв­ляется отношением эквивалентности, все пути разбиваются на классы связанных путей.

       Пусть 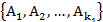 первый класс,  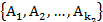-второй класс и так далее. Поскольку события  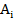и 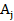из разных классов независимы,

…

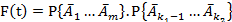       Если число путей в классах невелико, то вероятности в правой части легко вычисляются.

       Введем теперь понятие сечения. Множество элементов 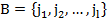 -называется сечением, если:

       а)    Система неисправна, если неисправны все элементы сечения независимо от состояния других элементов.

       б)    Никакое подмножество B не обладает свойством (а).

Пусть 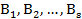 - все сечения. Событие, состоящее в том, что все элементы неисправны обозначим той же буквой  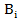. Тогда: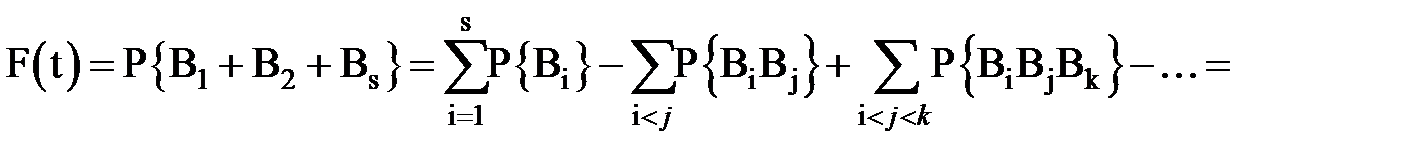

               

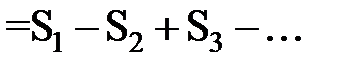
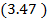
   Обычно вероятности 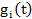на интересующем нас участке времени малы.   Знакопеременная сумма 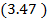обладает таким свойством для любого k :

,

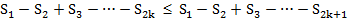     то есть 

,   

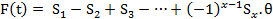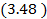
     где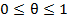   

     Если:

,

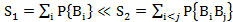то справедлива приближенная формула:

       .                      

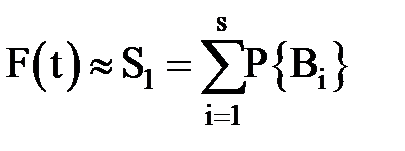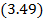
       Если такого приближения недостаточно, можно взять еще нес­колько слагаемых 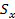, использовав оценку  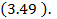Саму сумму 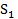, также можно оценить. Допустим, что все  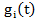одного порядка , 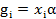,  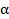- малый параметр. Тогда любая вероятность  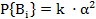, где x - число элементов в сечении. В этом случае в сумме 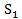мы можем ограничиться самыми короткими сечениями, у которых x минимально, грубо оценив все остальные слагаемые.       

Рекуррентный метод

       Часто для расчета надежности можно использовать рекуррентный метод, суть которого состоит в следующем.

       Допустим, что оценивается  надежность системы. Будем рассмат­ривать нашу систему 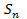как       n -ый член некоторой последовательности систему  в которой каждая последующая система получается из предыдущей добавлением нескольких элементов, множество состояний каждой системы 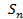 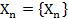мы выбираем так, чтобы:

       а)    по состоянию системы 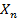 мы могли однозначно сказать работоспособна  система или нет;

       б)    последовательность состояний систем 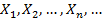 образовывала марковскую цепь, то есть, чтобы по известному со­стоянию  n-ой системы  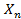однозначно определялись вероят­ности состояний системы  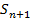. Конечно, если взять 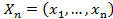,    задать состояния всех эле­ментов системы, то эти два условия будут выполнены. Но очень часто удается выбрать пространство с гораздо меньшим числом со­стояний, для которого условия (а) и (б) выполняются. Тогда можно для расчета надежности воспользоваться обычными методами теории марковских цепей.

       Приведем два примера.

1) Пусть система имеет вид (см. рис. 3.6):

1          2           3

B

n

A

Рис. 3.6. Интерпретация системы из n   элементов

       Для удобства понимания будем интерпретировать систему так: элементы - это линии , по которым подается вода; из А по двум линиям она поступает на первые два пункта, каждый из этих пунктов передает ее по двум линиям на следующие два пункта и т.д. Вероятность отказа каждой линии равна g , сами пункты связи считаются безотказными. Каждая из двух вход­ных и двух выходных линий тоже считается безотказной. Система 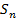, состоящая из 4 ( n-1 ) элементов (линий связи) ис­правна, если вода поступает   из А в В.

       Возьмем в качестве пространства состояний системы

,

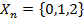       Состояние 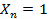означает, что информация не поступает на і конечных пунктов. Ясно, что последовательность, образует однородную марковскую цепь.

       Переходные вероятности

, ,

,    ,

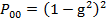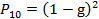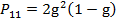Других переходных вероятностей можно не вычислять, так как со­стояние 2 является поглощающим.

       Пусть ,     ,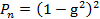

       тогда 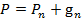 - вероятность безотказной рабо­ты системы . Вероятност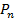и и 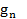удовлетворяют рекуррентным уравнениям (уравнения Колмогорова):

 ,

 ,

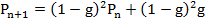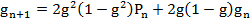       с начальнальными условиями .

       Решая  эти уравнения, получим:

,

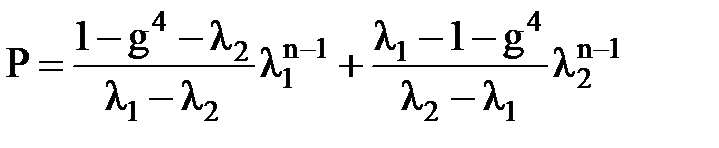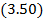
       где 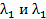 - корни уравнения

,

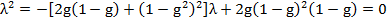       откуда:

,

,

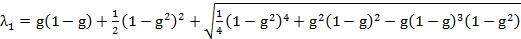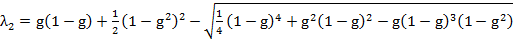       При 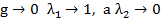, поэтому при молом  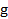 даже не очень большом  n  вторым слагаемым в ( 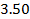) можно   пренебречь.

       Раскладывая 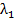 и 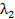 по степеням 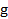, получим:

   

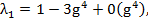
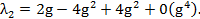
       C некоторым приближением  получается:

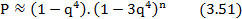
Ветвящаяся система

       Ветвящаяся система S _n имеет следующий вид (см. рис.3.7):

 

 

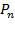
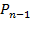
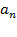
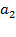
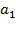
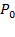
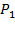
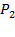
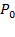
Рис.3.7. Схема ветвящейся системы

 

       Головной элемент, имеющий функцию надежности 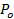 , управляет 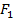одинаковыми элементами первого ранга с фун­кцией надежности  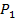     , каждый из них управляет  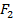элементами второго ранга, у всех элементов второго ранга с функ­цией надежности  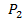и так далее.

       Отказ каждого элемента выключает из работы все элементы, сле­дующие за ним. Элементы последнего n-го ранга называются выходными, их число равно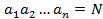

       Таким образом, выходной элемент может не работать либо пото­му, что он сам отказал, либо потому, что отказал один из пред­шествующих ему элементов. Система 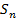 считается отказавшей, если число работающих выходных элементов стало меньше некото­рого критического числа in.

       Здесь в качестве состояния системы S_n    можно взять число работающих выходных элементов. Обозначим его .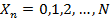

       Последовательность образует марковскую цепь. Эта цепь будет неоднородной. Она является частным случаем дискретного ветвящегося процесса Гальтона-Ватсона и исследовать ее проще всего методом производящих функций [10, 23 ].

       Пусть

.

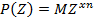       Обозначим 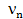 - биномиальную случайную величину

, ,

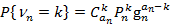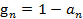это есть вероятность того, что из , элементов n -го ранга, управляемых одним элементом предыдущего ранга, не отка­зало k элементов. Производящая функция биномиальной вели чины

,   

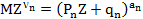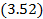
        Заметить, что

,

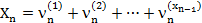       где 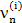 - независикы и распределены по закону (3.52).

       Тогда по формуле полных вероятностей

                                                                                                        

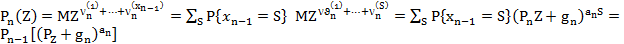
       Итак,

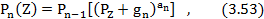
причем

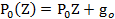
       Эта рекуррентная формула позволяет   найти произ­водящую функцию 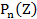,  но при большом числе выходных элементов она малоэффективна. Однако, моменты величины  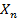 находятся довольно просто:

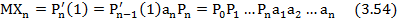
       С большими вычислениями, но все же в обозримой форме находятся 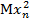,  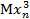и так далее.

       Учитывая это обстоятельство, можно предложить следующий ме­тод приближенной оценки функции надежности системы:

                                                                                   

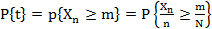
Как известно из анализа,

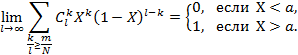
Но тогда:

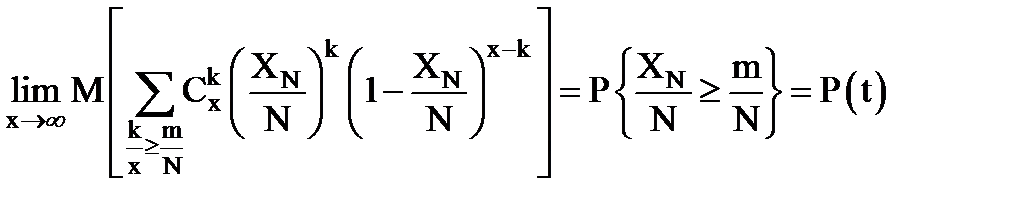
При достаточно большом  l  (при l ³ 3 ) справедлива приближенная формула

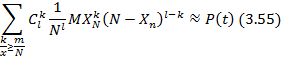
где левая часть выражается через моменты  X_n  порядка, не выше l .

  3.4.4.Модели зависимости элементов

       В системах без восстановления очевидно допускать  наличие зависимости отказов элементов в си­стеме.  

       1.Дискретная зависимость.

       Предположим, что каждый элемент может находиться в трех со­стояниях - состоянии простоя, состоянии работы и состоянии от­каза .

       Состояние отказа - необратимое, т.к. элементы невосстанавливаемые. Состояние всех элементов задается троичным вектором  

n=(n_1, n_{2, × × ×} n_n),

       где 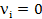 - простой,  - работа, 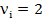 - отказ –го элемента.

       Допустим, что отказ элемента может быть собственным и несобственным.   Каждый і-тый элемент имеет некоторый ресурс 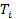и его собственный отказ наступает тогда, когда суммарное время работы, то есть суммарное время, проведенное в состоянии (1) достигает величины .

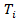2

n

1

           

 

 

Рис. 3.8. Интерпретация перехода элемента в состояние: простоя, работы, отказа  

       Несобственные отказы (переходы 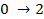 и 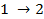),а также переходы из рабочего состояния в состояние простоя и обратно (переходы  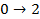и 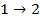) могут происходить только в моменты собственных отказов элементов(см. рис. 3.8). Причем перехо­дить из состояния в состояние в эти моменты могут с некоторыми заданными вероятностями целые группы элементов.  

       2. Холодное резервирование.

       Пусть имеется n одинаковых элементов с вероятностью отказа 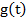. В момент t= 0 первый из включаемых в работу , а остальные в выключенном состоянии образуют холодный резерв.  В момент от­каза работающего элемента включается первый резервный, после его отказа второй и так далее. Система отказывает, когда отка­зывают все n элементов.  Время жизни системы:

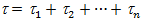
       где 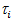- время работы i -го элемента.

       Вероятность отказа системы 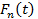определяется реккурентно

      

,

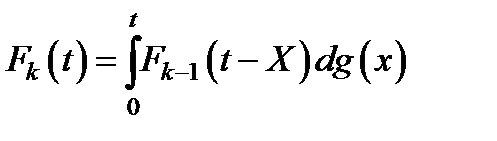
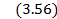
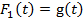       а среднее время жизни системы

 ,     

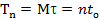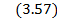
       где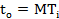

       Если элементы стареющие, то сама система тоже будет старею­щей. Кроме того  справедли­ва оценка:

    

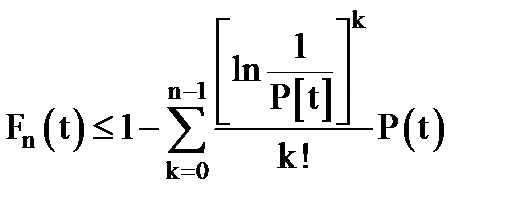
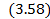
       где .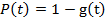

       Эта оценка удобна тем, что в отличие от 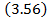она не требу­ет знания промежуточных  значений функции 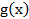, , 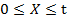достаточно знать .

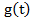       3. Зависимость начальных параметров.

       Время безотказной работы изделия определяется двумя фактора­ми - значениями начальных параметров изделия и параметрами ре­жима, в котором работает это изделие. Отказы элементов могут быть зависимыми из-за того, что они входят в состав одной систе­мы и на них действует общий случайный режим . Но отказы элементов могут быть зависимы и потому, что зависимы их начальные параметры - этот тип зависимости почти никогда не учитывается .  Не будем развивать никакой теории, а ограничимся примером.

       Пусть завод поставляет  одинаковые трубы, из кото­рых  монтируется трубопровод из 100  труб (элементов) . На заводе  периодически возникают неполадки,  обнаруживаемые не сразу. За период от начала неполадки  до ее об­наружения с завода поставляется  в среднем 100 дефектных  труб (элементов) , которые отказывают в системе вскоре после начала работы. Пред­положим, что остальные трубы, изготовленные в период нормальной работы завода  практически безотказны. После обнаружения неполадки  дефект устраняется  и завод  продолжает нормально работать. Допустим,  за  время неполадки изготавливается  в среднем 100.000  труб. Если   из большой партии труб  (например, продукция за год) взять  равномерно распределенную по множеству элементов выборку и провести  испытания, то   по­лучим, что вероятность отказа трубы  равна:

, а вероятность отказа трубопровода (системы из последовательных элементов)

 .

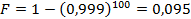        При сложившихся  условиях поставки труб на объекты можно допустить, что   группа дефектных труб  может попасть  на один, максимум  на два объекта и поэтому истин­ная вероятность отказа трубопровода  равна  .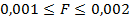           

       Эту разницу мы получили потому, что в первом случае пренебрегли зависимостью отказов.        Этот   утрированный пример имеет своей целью обра­тить внимание инженера  на то, что зависимость начальных пара­метров следует как-то учитывать при расчете надежности, особенно надежности оборудования, объектов систем водоснабжения.

       4. Зависимость отказов из-за общего режима.

        Обозначим  режим работы системы 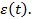Допустим, что элементы соединены в системе последовательно и при фиксированной траектории 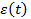от­казывают независимо. Тогда, если  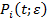- условная вероятность безотказной работу при условии, что фиксирован ре­жим 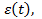то функция надежности системы:

 ,     

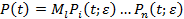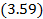
где усреднение берется по всем траекториям режима. Безусловная функция надежности і -го элемента равна:

и, как видно из 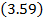  вообще говоря,

 ,

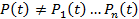       Для того, чтобы воспользоваться формулой 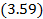, надо, во-первых знать, как зависит надежность от режима, и, во-вторых, как рас­пределен случайный процесс 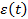. Однако, даже не зная распределения процесса 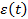, можно получить одно полезное неравенство.

       Предположим, что справедлива гипотеза линейного накопления повреждений. Тогда (см. § 4 гл. 1):

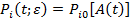, где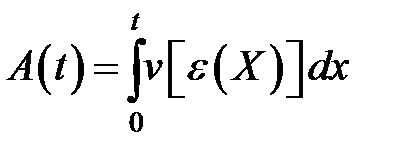

       Пусть 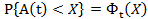- функция распределения случайной величины А(t).   Тогда из 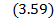следует:

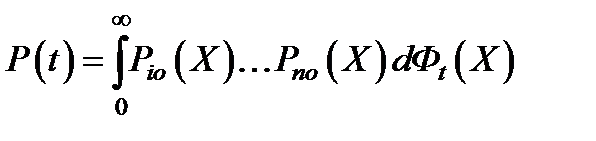и

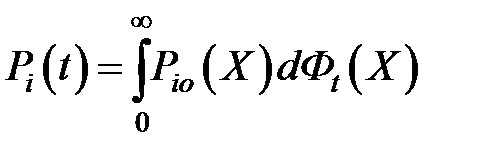
       Существует одно малоизвестное неравенство Чебышева [23] :

если функции 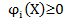монотонно убывают, a F(Х) - функция распределения, то:

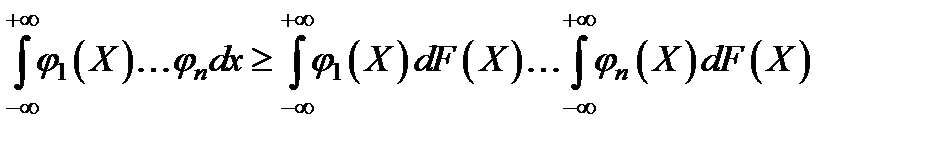   (3.60)

       Применяя его к нашему случаю, получим:

 ,

то есть, рассчитывая надежность в предположении независимости элементов, мы несколько занижаем истинную надежность.

       5.Случай зависимости надежности элементов от состояния других элементов.

       Пусть состояние элементов определяется   двоичным вектором 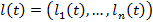, траекторию процесс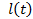а  на 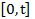обозначим  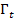. Если предположить, что нет зависимости начальных параметров элементов и нет зависимости отказов из-за общего случайного режима (например, режим детерминированный), то единственным возможным типом зависимости может быть зависимость надёжности одного элемента от отказов других элементов. Отказы элементов могут приводить к дополнительному износу другого  элемента.

       Например, в момент отказа возникает гидравлический удар, который меняет скачком давление в сети.  При увели­чении давлния , нагрузка передается  на другие элементы. Если эле­менты функционально заменяемы, то при отказе одного элемента другие берут на себя дополнительную нагрузку, отчего их надеж­ность, естественно, падает.

       Наконец, отказы одних элементов могут включать   или выключать другие элементы (насосные установки, запорная арматура, трубопроводы).

       Трудно описать все возможные проявления такой зависимости, но ясно, что в самом общем случае эту зависимость можно описать так: если фиксирована траектория процесса 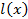 до момен­та t , то вероятность перейти за время  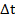из со­стояния 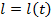в состояние  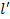  равна:

.

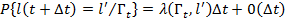       Эта формула учитывает и возможность появления в один момент нескольких отказов. Более частным является случай, когда в каждый данный момент может произойти только один отказ. В этом случае процесс  задаетсяинтенсивностями отказов элементов .

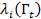 - условная интенсивность отказа i-го элемен­та при условии, что фиксирована траектория процесса до момента t . Еще  предполагается , что вероят­ность появления более одного отказа на  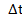 есть 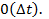Cледующим является тот случай, когда интенсивность отказа эле­мента зависит от времени t и от состояния процесса в момент t; .

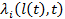       В этом случае процесс будет марковским. Наконец, последний случай - это случай, когда интенсивности при фикси­рованном 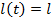не зависят от времени:  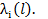 Отметим , что если из­вестно одномерное распределение процесса

.

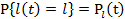то в силу монотонности функции 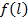- состояния си­стемы -  находится и функция надежности системы

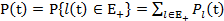 , (3.62)

( монотонность 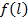 означает, что система, отказав, не может восстановиться из-за появления до­полнительных отказов элементов).

       6.Процесс чистой гибели.

       Рассматривается случай, когда интенсивность отказа элементов зависит только от состояния этих элементов в данный момент 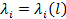  .Но предварительно   рассмотрим  случай, когда элементы входят в систему симмет­рично, то есть  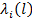не зависит от номера i (все элементы одинаковы),  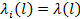 и функция 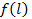не меняется при любой перестановке координат вектора l. В этом случае интенсивность  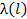и функция 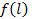зависят только от числа отказавших элементов:

,

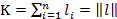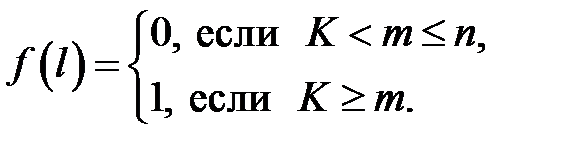
       Тогда вместо процесса  мы можем рассмотреть процесс 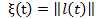, это число неисправных элементов в момент t.

       Вероятность перехода из состояния K в состояние ( К + і) за время 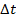 равна,  

,

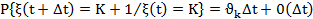       где 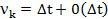,  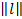     = К

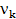        - это суммарная интенсивность отказа оставшихся в живых ( n - К ) элементов.        Получившийся марковский однородный процесс с состояниями 0,1,...,  в котором мгновенные скачки воз­можны только вверх на одно состояние, называется процессом чис­той гибели.  Поскольку рассматривается только поведение процесса до момента отказа системы,  поэтому состояние m   будет по­глощающим, поскольку попав в состояние  при 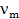=0 , процесс навсегда в нем останется.

       Введем вероятности состояний:

Р_к (t)= Е { x (і) = K },

 очевидно также, что вероятность отказа системы равна

F(t)= Pt).    (3.63)

       Для вероятностей состояний легко составляются уравнения Колмо­горова:

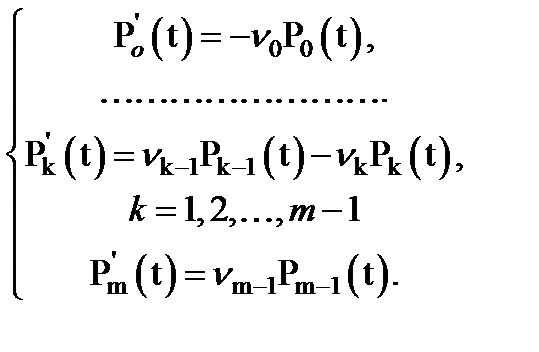(3.64)

                    

       Так как в начальный момент    t = 0     в системе исправны все элементы (это обычное предположение), то

Р _o ( o )=1, Р _k ( o )=0, K > 0

       Применяя к этой системе преобразование Лапласа А.Д. в работе [ 23] доказано , что для расчета надежности можно пользоваться приближенной формулой :

F ( t ) = 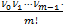t^m          ( 3.65)      

 относительная погрешность  при этом не превысит

 

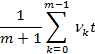
        Отметим еще такую очевидную интерпретацию  данной  модели - время до отказа системы T есть сумма независимых величин

,

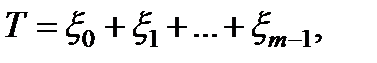
где   Р{ x _k > t }= ,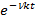

это следует из того, что время пребывания процесса в каждом состоянии К имеет показательное распределение с параметром n k . Отсюда, в частности, мгновенно получается  

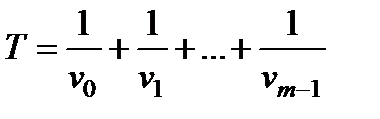      (3.66)

       Изученный процесс чистой гибели включает в себя довольно много реальных моделей резервирования без восстановления. Пусть резервная группа состоит из m элементов - один рабочий, остальные резервные. При отказе рабочего элемента на его место мгновенно включается резервный элемент. Система отказывает, ко­гда отказывают все элементы (например, противопожарные системы водоснабжения).  Пусть l - интенсивность от­каза рабочего элемента, l^' - интенсивность отказа каждо­го резервного элемента. Процесс  x(t) - число отказавших  элементов к моменту t   - будет   процессом чистой гибели, если взять

n _k = l +( m -1) l ^'

       При  l^'= 0 получаем холодный резерв, при l^' = l  горячий резерв, а в случае, когда l^' <l  ,       - теплый ре­зерв. Существуют и другие модели, которые описываются процессом чистой гибели.

       7. Обобщенный процесс чистой гибели.

Рассмотрим случай, когда интенсивность отказа i -го эле­мента -  l_i ( l ).  Поток отказов элементов системы относится к мар­ковскому однородному процессу   l ( t ) . Но это процесс многомер­ный и уравнения Колмогорова выглядят  для  него весьма громоздко. Не приводя дальнейших подробностей , отметим, что оценивать  надежность такой системы, с небольшой погрешностью , можно  [23 ] по формуле

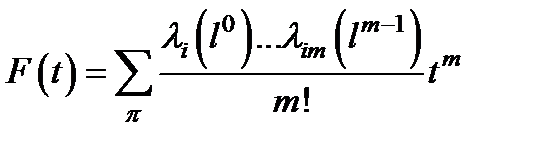 (3.67)

       где m – количество элементов в системе;

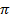        - путь;

       l _i ( l ) t – интенсивность отказов на участке времени t очень мала, т.е.

      l _i ( l ) - интенсивности положительны и фиксированы, а t ® 0.

       Средене время жизни системы будет равно

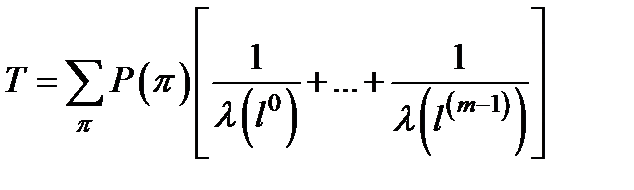        ( 3.68)