1. Описание системы.
Рассмотрим систему, состоящую из n элементов, каждый из которых работает, отказывает, сразу же после отказа восстанавливается, после восстановления возвращается на свое место и включается в работу, снова отказывает и так далее. Состояние элементов в каждый момент времени задается двоичным вектором 
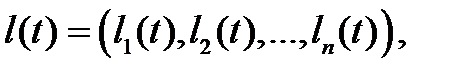
Состояние системы задается функцией

Как и выше, мы предполагаем, что функция f удовлетворяет условию :
из 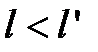 следует
следует 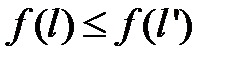 .
.
Пусть 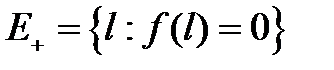 - множество исправных состояний системы,
- множество исправных состояний системы,
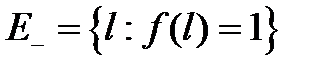 множество неисправных состояний системы.
множество неисправных состояний системы.
Пусть l = (l 1 , l 2, .., li -1, 0 , li +1, ... ln ).
Определим вектор 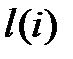 так:
так:
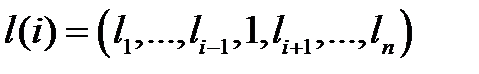
то есть вектор 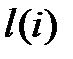 получается из l при отказе i-го элемента.
получается из l при отказе i-го элемента.
Назовем состояние 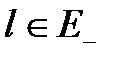 граничным неисправным состоянием, если существует
граничным неисправным состоянием, если существует 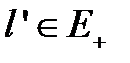 и номер i такой, что
и номер i такой, что 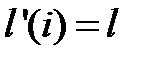 . Другими словами, в граничное неисправное состояние мы можем попасть из
. Другими словами, в граничное неисправное состояние мы можем попасть из 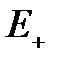 при отказе одного элемента. Множество граничных неисправных состояний обозначим
при отказе одного элемента. Множество граничных неисправных состояний обозначим 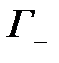 . Определим условие при котором отказывают элементы в системе.
. Определим условие при котором отказывают элементы в системе.
Пусть в момент t система находится в состоянии 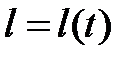 . Допустим, что вероятность отказа i -го элемента на интервале
. Допустим, что вероятность отказа i -го элемента на интервале 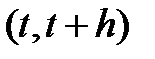 равна
равна
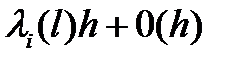 (3.129)
(3.129)
и не зависит от поведения процесса l (x) момента t, а вероятность появления более одного отказа на (t, t+h) есть ( h ) , то есть исключаются групповые отказы. Условие (3.129)выполняется с достаточной точностью если сами элементы являются достаточно сложными устройствами, так как тут действует предельная теорема Григелиониса ( см. § 3 гл. П) .
Если же элементы - простые, то они обычно входят в системы большими симметричными группами, поток отказов от этой группы по той же теореме Григелиониса будет пуассоновским (условие постоянства) и поэтому опять условие (3.129)должно выполняться. Правда, с течением времени система может изнашиваться стареть и интенсивности 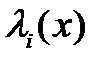 будут тогда зависеть от времени -
будут тогда зависеть от времени - 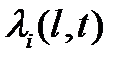 . Но обычно интенсивности с течением времени меняются медленно и на не очень большом участке времени их можно считать постоянными.
. Но обычно интенсивности с течением времени меняются медленно и на не очень большом участке времени их можно считать постоянными.
Отметим 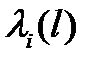 , если l i =1 , то есть і -тый элемент в состоянии l неисправен.
, если l i =1 , то есть і -тый элемент в состоянии l неисправен.
Обозначим 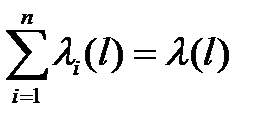 и допустим, что для любого
и допустим, что для любого 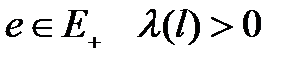 , иначе система становится безотказной. После отказа элемент мгновенно поступает на восстановление. Количество ремонтных единиц - r . Дисциплина восстановления элементов может быть произвольной - не все ремонтные единицы могут быть доступны для данного элемента (например, ремонтные рабочие могут иметь разную специализацию) , при ремонте среди элементов может быть установлен приоритет, восстановление элементов может прерываться из-за поступления более важного отказавшего элемента и т.п. Но ставятся условия:
, иначе система становится безотказной. После отказа элемент мгновенно поступает на восстановление. Количество ремонтных единиц - r . Дисциплина восстановления элементов может быть произвольной - не все ремонтные единицы могут быть доступны для данного элемента (например, ремонтные рабочие могут иметь разную специализацию) , при ремонте среди элементов может быть установлен приоритет, восстановление элементов может прерываться из-за поступления более важного отказавшего элемента и т.п. Но ставятся условия:
а) каждый элемент имеет хотя бы одну доступную для него ремонтную единицу и, если в момент отказа элемента имеется хотя бы одна свободная и доступная для него ремонтная единица, то он мгновенно поступает на одну из них;
б) ремонт элемента может прерываться при поступлении других отказавших элементов, однако суммарное время ремонта 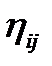 имеет всегда одно и то же распределение
имеет всегда одно и то же распределение
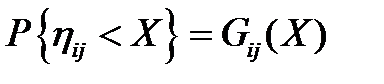 , (3.130)
, (3.130)
где i - номер элемента, j - номер ремонтной единицы, на которую поступил отказавший элемент (здесь мы учитываем, что ремонтные рабочие могут иметь разную квалификацию).
Допустим, что 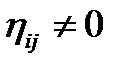 . В начальный момент система полностью исправна, то есть
. В начальный момент система полностью исправна, то есть 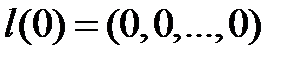 .
.
Задача заключается в нахождении распределения момента первого отказа системы 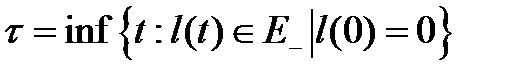 .
.
Если интервалы времени ремонта будут распределены экспоненциально, то есть
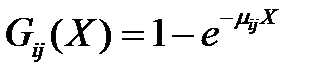 , (3.131)
, (3.131)
то процесс 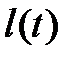 будет Марковским. Однако, как показывают статистические данные, время ремонта почти никогда не имеет показательного распределения. При допущении (3.131) сильно искажаются характеристики надежности. С другой стороны, в реальных условиях время ремонта, обычно, очень мало по сравнению с интервалом между соседними отказами элементов. Поэтому естественно исследовать асимптотическое поведение величины
будет Марковским. Однако, как показывают статистические данные, время ремонта почти никогда не имеет показательного распределения. При допущении (3.131) сильно искажаются характеристики надежности. С другой стороны, в реальных условиях время ремонта, обычно, очень мало по сравнению с интервалом между соседними отказами элементов. Поэтому естественно исследовать асимптотическое поведение величины 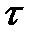 , когда время ремонта в некотором смысле стремится к нулю, и, как следствие, получить приближенные формулы для характеристик надежности. Авторамим [10, 23 ] доказано, что если время ремонта элементов в среднем мало по сравнению со временем между соседними отказами элементов, то для оценки вероятности безотказной работы системы можно пользоваться приближенной формулой:
, когда время ремонта в некотором смысле стремится к нулю, и, как следствие, получить приближенные формулы для характеристик надежности. Авторамим [10, 23 ] доказано, что если время ремонта элементов в среднем мало по сравнению со временем между соседними отказами элементов, то для оценки вероятности безотказной работы системы можно пользоваться приближенной формулой:
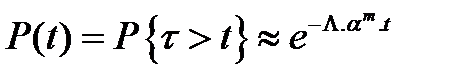 , (3.132)
, (3.132)
где 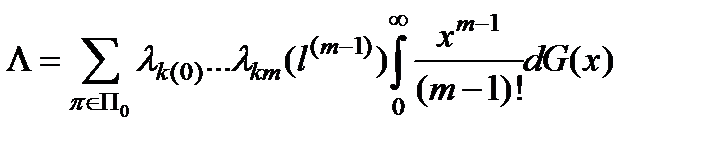 .
.
Дата: 2018-12-21, просмотров: 378.