Статистической гипотезой называют всякую гипотезу, которая относится к законам распределения или параметрам закона распределения случайных величин и которая может быть проверена статистически, т.е. ко результатам выборочных наблюдений.
Статистические гипотезы могут быть отнесены или к распределениям случайных величин, или к их числовым характеристикам.
В первом случае при проверке статистических гипотез приходится решать два вида задач:
- когда проверяются гипотезы о законах распределения случайных величин т.е. проверяют различие (или сходимость) между статистическим распределением и распределением генеральной совокупности;
- когда проверяется однородность двух (или более) статистических (выборочных) распределений, т.е. проверяется гипотеза, что оба выборочных распределения характеризуют одну генеральную совокупность.
Во втором случае, - при проверке гипотез относительно числовых характеристик или параметров законов распределения, -могут решаться следующие задачи
-когда сравниваются средние значения выборочной совокупности и генеральной совокупности (случайно ли расхождение между ними или расхождение существенно);
- когда проверяется гипотеза о равенстве дисперсий выборочной и генеральной совокупности;
- когда проверяется гипотеза о равенстве средних значений двух или более выборочных наблюдений;
- когда проверяется статистическая гипотезе о равенстве двух или более выборочных дисперсий,
При проверке статистических гипотез выдвигаются две гипотезы:
Но - нулевая гипотеза; т.e. такая гипотеза, которая подтверждает выдвинутое предположение, например, что расхождения между характеристиками случайны и Н1 - альтернативная (противоположная) гипотеза, которая отвергает сделанное предположение, т.е., что расхождения неслучайны, существенны.
Проверка статистических гипотез осуществляется в следующей последовательности [4,15] :
а) В соответствий с решаемой задачей формулируется критерий R . В общем случае критерий R является функцией выборочных наблюдений т.е.
R = R {Fn ( x1, x2, · · · xn; q )}
R = R { 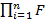 ( xi ; q )} ( 5. 1 )
( xi ; q )} ( 5. 1 )
б) По результатам и выборочных наблюдения вычисляется значение критерия R.
в) Вычисленное значение критерия R со значением этого критерия, устанавливаемого в соответствии с выдвинутым предположением.
Рассмотрим геометрическую интерпретацию поставленной задачи. Критерий R , являющийся функцией выборочных наблюдений, представляет собой случайную величину, следовательно, он может описан некоторым законом распределения (рис. 5.1).
| f(R) |
| R |
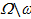
|
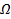
|
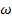
|
Рис. 5.1. Плотность вероятности наблюдения велчины R
Обозначим W - область возможного изменения критерия. Рассмотрим область w , отсекаемую некоторой прямой, при этом значение критерия в этой точке обозначим R a , а оставшуюся область - через W - w = W \ w (знак \ означает исключение).
Говорят, что гипотеза Но справедлива, если значение статистического критерия R попадает в область W \ w т.е.
Но : R Є W \ w (5.2)
Если справедлива гипотеза Н1, то критерий R попадает в критическую область w, т.е.
Но : R Є w (5.3)
В связи с тем, что значение критерия R величина случайная, поэтому может оказаться, что R попадает в критическую область, хотя справедлива гипотеза Но и, наоборот, R попадает в область W \ w , хотя справедлива гипотеза Н1.
Следовательно, при проверке гипотез может быть совершено два вида ошибок.
Ошибка первого рода возникает в тех случаях, когда справедлива гипотеза Но, но , но критерий R попадает в критическую зону w. Вероятность такой ошибки обозначается через a .
Ошибка второго рода состоит в том, что справедлива альтернативная гипотеза Н1 , но значение критерия R попадает в область W \ w. Вероятность такой ошибки обозначается через, b.
Вероятность ошибки первого рода определяется из соотношения
Р {R Є w / Но } = a (5.4)
В этом случае величина a называется уровнем значимости.
Вероятность ошибки второго рода определяется по формуле:
Р { R Є W \ w / Н1} = b (5.5)
При проверке гипотез возникает проблема выбора уровня значимости a
При уменьшении a вероятность отвергнуть нулевую гипотезу Но уменьшается, но при этом растет β , т. е. увеличивается вероятность ошибки второго рода - принять гипотезу, когда она неверна.
Выбор критической области и представляет собой сущность решения задачи о проверке статистических гипотез.
При решении ряда практических задач одному и тому же уровню значимости a могут соответствовать различные критические области.
Рассмотрим эту задачу на примере t - критерия :
Первый случай. Область больших положительных отклонений (рис. 5.2)
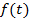
|
| t |
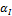
|
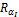
|
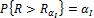
|
Рис.5.2. Область больших положительных отклонений
Второй случай. Область больших отрицательных отклонений (рис. 5.3).
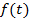
|
| t |
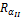
|
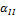
|
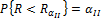
|
Рис. 5.3 .Область больших отрицательных отклонений
Третий случай. Двухсторонняя область отклонений (рис. 5.4).
|
|
| t |
|
|
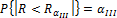
|
Рис. 5.4. Двухсторонняя область отклонений
Критическая область выбирается в соответствии с решаемой задачей. Для выбора критической области в статистике введено понятие мощности критерия. Под мощностью критерия понимают вероятность того, что значение вычисленного критерия попадает в критическую зону, если верна конкурирующая гипотеза. По статистическим данным вычисляется критерий R. Если верна альтернативная гипотеза Н1, то вычисление значение критерия R попадает в критическую область, т.е.
Р {R Є w / Но } = g (5.6)
Величина γ и является характеристикой мощности критерия, γ = 1-β.
При правильном выборе критической области эта вероятность должна иметь максимальное значение.
Чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода.
В статистике различают два вида гипотез:
а/ непараметрические гипотезы и критерии. Применение их не
требует знания законов распределения случайных величин. В качестве таких критериев, например, используется c2 -критерий (Пирсона), λ - критерий (Колмогорова), W - критерий (Вилкоксона) и т.д. Точность (качество) проверки гипотез с помощью непараметрических критериев всегда ниже по сравнению с параметрическими критериями.
б) параметрические гипотезы и критерии. Они основаны на знании законов распределения случайной величина. Эти критерии, как правило, используются для проверки однородности средних и дисперсий. К ним относятся: t - критерий (Стьюдента), для проварки однородности средних; F - критерий (Фишера) - для проверки однородности дисперсии двух групп наблюдений; M -критерий (Бартлетта) - для проверки однородности нескольких дисперсий, когда объемы наблюдений различны; G -критерий (Кочрена),
когда объемы выборки одинакова; L-критерий (Неймана-Пирсона) используется для проверки однородности нескольких средних.
Дата: 2018-12-21, просмотров: 463.