Требования к информации

       Своевременная регистрация всех происходящих в процессе эксплуатации повреждений элементов систем водоснабжения и сбор необходимых сведений  о причинах их возникновения  представляют собой единственный возможный источник информации для получения обоснованных численных показателей   надежности водопроводных объектов.  Для накопления требуемых статистических сведений о повреж­дениях элементов водопроводных систем необходимо, чтобы  формы  регистрации неисправностей сооружений и оборудования были  по возможности простыми и предельно унифицированными для всех  организаций эксплуатирующих данные объекты.           Поэтому разработка методов и форм регистрации повреждений имеет большое практическое значение. Качество информации  определяется ее достовер­ностью, полнотой, непрерывностью и оперативностью [ 25 ].

Достоверность достигается точным учетом всех отказов незави­симо от причины возникновения, последствий или трудоемкости  их устранения.   

Не менее важно и правильное определение причин отказов.   Достоверность информации в значительной степени  зависит от квалификации персонала, ведущего записи в журналах по эксплуатации оборудования и сооружений, а также  лиц, выполняющих обработку сведений об отказах объектов водоснабжения.  Полнота информации заключается в том, что собранные сведения  должны быть достаточны для решения поставленных задач. 

Объем информации определяется целями решения задачи, особенностями конструкции  и условий эксплуа­тации объекта.  

Для определения количественных показателей надежности и выявления причин отказов необходимо как мини­мум:

1) Сведения об отказавшем объекте  (наименование и тип от­казавшего устройства, узла, технологи­ческого агрегата, которые объединяет объект  или элемент);

2) Сведения о времени наступления отказа;

3) Сведения о наработке на отказ (моменты включения и от­ключения элемента);

4) Сведения о причине возникновения отказа.

5) Сведения об условиях восстановления

При оценке причин отказа  необходимы дополнительные сведения об условиях эксплуатации, режиме работы, ремонта объекта.

Сведения о потоках отказов

        Водопроводные сооружения и системы относятся к восстанавливаемым объектам. Оборудование или сооружение (насосные агрегаты, запорная арматура, трубопроводы и т.д.)  после каждого отказа ремонтирует­ся на месте или заменяется идентичным, причем моменты наступле­ния отказов являются случайными величинами. Последовательность отказов, возникающих  в случайные моменты време­ни, именуют  потоком.    

       Для математического описания потоков отказов обычно исполь­зуются модели теории потоков однородных событий и теории восстановления, изложенных в работах  [4,10, 23]. Описании этих моделей базируется на терминологии, которая используется в теории потоков отказов (потоков однородных событий).  

Обычно  число отказов на  про­межутке  времени (0, t ) обозначают как функцию  N (t ). Поток называется стационарным, если закон распределения N ( a + t ₁) - N ( a), N ( a + t ₂) - N ( a),   · · · N ( a + t _k) - N ( a) для любого конечного k ³ 1 зависит только от чисел t _1, t _{2 , · · ·} t _{k ,}  но не зависит от a ³0. Выполнение требования стационарности означает, что вероятно­стная структура потока не зависит от сдвига во времени. В част­ности, закон распределения числа отказов на любом промежутке времени (t₂ -t₁ ) не зависит от самих   значений t ₁ и t₂, а зависит только от их разности.

Поток называется потоком без последействия, если для лю­бой конечной системы попарно непересекающихся промежутков вре­мени Dt1, Dt2 , · · · Dtk, числа отказов на этих промежутках N (_Dt ₁ ), N (_Dt ₂ ), _{· · ·}  N (_Dt _k    являются взаимно независимыми слу­чайными величинами.

В частности, выполнение требования отсутствия последействия означает, что закон распределения числа отказов на любом проме­жутке времени не зависит or реализации потока до и после этого промежутка времени.

Поток называется ординарным, если

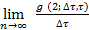 = 0,

где g(2; Dt ,  t ) = 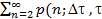) - вероятность получения по меньшей мере двух отказов на интервале времени [t, t +Dt ] .

 Ординарность означает практическую невозможность возникновения двух или более отказов одновременно.

Отметим возможность упрощения задания потока при выполне­нии требований стационарности и отсутствия последействия. Заме­тим сначала, что для любого потока задание распределения вектора

 Ведущая функция потока равна по определению

 w (t) = М [N (t)]                          (4.1 )

где М [N (t)] - математическое ожидание числа отказов за время t.

Приращение ведущей функции на отрезке времени [t, t] можно обозначить w (Dt, t) . Если w (t) дифференци­руема, то

u (t ) = 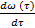 ,                ( 4.2)

называется   плотностью или интенсивностью потока.  

 Если w (t) < + 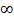 для t > 0, то поток называется финитным. Финитный поток называется регулярным, если для любого мо­мента времени выполняется условие

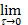р (0; 2 _D t ; t - _D t ) = 1,

где р (0; 2Dt; t- Dt) — вероятность не получить ни одного отказа в течение промежутка времени (0; 2Dt; t- Dt). Регулярность  озна­чает практическую невозможность возникновения отказов в заранее заданный момент времени.

Пуассоновские потоки

       Самым простым потоком является стационарный ординарный по­ток без последействия, который принято называть простейшим или однородным  пуассоновским. Он задается при помо­щи вероятностей  ):

P {N ( 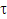 ) = n} = р (n ; 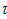)  (0 £ t < 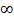; n = 0, 1, 2 )  (4.3 )

        В случае простейшего потока (выполняются требования ординарности, отсутствия последействия) и существует ведущая функция w (t), то поток задается  вероятностями получения n отказов  на   фиксированном отрезке t

p (t)= 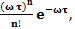     (4.4 )

     где   w -  математическое ожидание числа отказов на   отрезке времени  t , w = .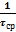

Выбор модели потока отказов

На этапе обработки статистической информации о надежности объекта водоснабжения первым возникает вопрос о выборе математической модели для описания его потока отказов.  От того, насколько правильно выбрана модель,  зависит  достоверность и точность полученных результатов.     

 Окончательное суждение о том, пригодна  предполагаемая модель для описания потока отказов, может быть сделано только на основании статистической проверки выдвинутой  гипотезы при помощи специальных критериев, некоторые из которых  будут рассмотрены ниже.  

Вопрос о выборе математической модели для описания потока в каждом конкретном случае может решаться на основе исследо­вания основных свойств реального потока: финитности, регулярно­сти, стационарности, ординарности и последействия. Наличие или отсутствие указанных свойств зависит от сложности объекта (оборудования), от условий работы и от вида отказа.

Перейдем к рассмотрению свойств потоков.

Финитность потока означает, что среднее число отказов на любом конечном отрезке времени должно быть конечно. Очевидно, что для любого реального потока это условие выполняется. 

Как уже отмечалось, регулярность означает практическую невозможность возникновения отказов в заранее заданный момент времени. Не будем рассматривать редкие случаи, кода для оборудования, установленного не качественно, это требование не выполняется. Например насос с отметкой выше уровня воды в источнике может не запуститься в работу при включении агрегата (не будим останавливаться на причинах). И обслуживающий персонал насосных станций допускает возникновение подобного события заранее.  Однако в большин­стве практических случаев отказы, возникшие в такие моменты времени, составляют небольшую долю процента по отношению к общему числу отказов и их влиянием можно пренебречь. Если же по какой-либо причине число таких отказов велико, их можно выделить из общего потока и обработать отдельно.

Требование ординарности также можно считать выполненным в большинстве практических случаев. Напомним, что требование ор­динарности означает практическую невозможность возникновения двух или более отказов одновременно. Поэтому причиной нарушения  ординарности в реальных потоках являются в основном вторичные отказы и переключения агрегатов, трубопроводов, сооружений. Отметим, что если на регуляр­ность потока влияли только заранее заданные моменты переклю­чений, то на ординарность влияют и случайные переключения, свя­занные, например, с отказами основного оборудования. Практика исследования потоков отказов насосных агрегатов  систем водоснабжения  показала, что неординарность незначительно влияет на  свойства потока   и этим влиянием без ущерба для точности статистических оценок  можно пренебречь.   Отказы, возникшие в моменты включения или изменения режимов основного оборудования, можно, как и в предыдущем случае, выделить из общего потока и рассматривать отдельно.

В этой связи, потоки отказов объектов водоснабжения (оборудования, сооружений, систем) практически можно считать финитными, регулярными и ординарными. Предположение об отсутствии этих свойств  у потоков  приводит, как правило, к  усложнению модели, а следовательно и статистических оценок.

 В то же время  необоснованно принятые предположения об отсутствии последействия и стационарности  могут привести к значительным ошибкам при обработке статистической информации, определении и использовании показателей надежности

Одной из основных причин наличия нестационарности и последействия в потоке событий следует считать влияние на любом объекте различ­ных воздействий человека.

 Воздействия человека, изменяющиеся во времени по определен­ному (не случайному) закону, приводят к нестационарности. К та­ким воздействиям можно отнести отключения технологического оборудования, сооружений; наличие периодов приработки после пуска оборудования в эксплуатацию и после ремонтов; изменение условий эксплуатации во времени;  изменение  режима работы основного оборудования по плану- графику и т.д.

Случайные внешние воздействия обусловливают последействие в потоках. В качестве примеров случайных воздействий, вызываю­щих последействие, можно привести случайные отключения оборудования  при  ошибках персонала, отказах вспомогательного оборудования (например,  при переключениях насосных агрегатов, трубопроводов); случайные воздействия человека при выполнении ремонтных работ   т. д.   При слу­чайном изменении условий эксплуатации меняется и интенсивность потока отказов. Условия эксплуатации, а следовательно, и интен­сивность потока отказов не могут меняться мгновенно. Если на каком-либо отрезке времени интенсивность, имеет повышенное зна­чение, то более вероятно, что на смежном отрезке интенсивность потока также будет иметь повышенное значение, и наоборот. Как показывает практика, дисперсия числа отказов в таком потоке будет больше, чем в случае неизменных условий работы.

 При прогнозировании  потока, говоря о том, что поток нестационарен, будем иметь в виду, что нестацнонарность потока во времени задана не случайным образом  или ее можно рассчитать по имеющимся данным. Если же известно, что имеются какие-либо   воздействия, влияющие на поток, или закон изменения этих воздействий во времени не задан, или не удается рассчитать закон изменения  во времени характеристик потока по имеющимся сведениям о внешних воздействиях, или закон изменений внешних воздействий задан как случайный, в потоке следует предполагать последействие. При статистической обработке для того, чтобы рассматривать поток как нестационарный, достаточно знать неслучайный закон изменения воздействий во времени , а определение зависимости характеристик потока от воздействий можно считать задачей статистического исследования потока. Поэтому при статистической обработке преимущественное применение находят модели нестационарных потоков, в то время как при прогнозировании более широкое приме­нение находят потоки отказов с последействием.

В качестве примера рассмотрим прогнозирование потока отка­зов технологического оборудования в целом. Если бы от­ключения оборудования производились только по заранее заданному графику, например, при капитальных ремонтах агрегатов, то такой поток можно было бы рассматривать как неоднородный пуассоновский с интенсивностью и( t), пропорциональной количеству работаю­щих агрегатов. Так как заранее нельзя предусмотреть все отключения агрегатов, например, при авариях, то такой поток приходится рас­сматривать как поток с последействием, причем если плановые остановки агрегатов в течение рассматриваемого промежутка времени не предвидятся, то поток можно считать стационарным, так как вероятность остановки агрегата вследствие аварии для любого мо­мента времени одинакова. В то же время при статистической обра­ботке потока, т. е. при обработке реализации потока, все отклю­чения можно учесть и рассматривать поток как нестационарный.

Следующей причиной, в результате которой в потоке появляется нестацнонарность и последействие, является отличие законов рас­пределения отдельных элементов от экспоненциального. Отличие за­конов распределения элементов от экспоненциального по-разному сказывается на свойствах потока в зависимости от сложности и состава оборудования и вида отказа.

Рассмотрим сначала поток отказов одного восстанавливаемого элемента. В этом случае вероятность безотказной работы зависит только от момента возникновения последнего отказа, а законы рас­пределения времени между отказами можно считать одинаковыми. Заметим, что последействием, обусловленным случайными внешними воздействиями, в случае потока отказов одного элемента часто можно пренебречь. Это допущение основано на том, что частота изменении внешних воздействий, как правило, больше частоты вос­становления. Кратковременные отключения элементов можно рас­сматривать как случайные изменения режимов работы. Поэтому зависимость между наработками отдельных элементов будет незна­чительна и все предпосылки модели потока восстановления оказы­ваются выполненными.

Выше уже отмечалось, что интенсивность потока восстановле­ния устанавливается не сразу. Поэтому для того, чтобы опреде­лить установившееся значение интенсивности потока отказов, дли­тельность испытаний должна быть достаточно велика или испыта­ния должны начинаться после того, как поток установится. Иначе говоря, испытания должны начинаться не в момент отказа, а в про­извольный момент времени, не зависящий от моментов возникнове­ния отказов. Поток отказов в этом случае можно считать стацио­нарным.

Если на испытаниях находится не один элемент, а группа одно­временно установленных элементов, то испытания должны начи­наться после того, как поток установится, или проводится доста­точно длительное время. Необходимо отметить, что практически при испытаниях на надежность в условиях эксплуатации наблюдение ведется над оборудованием, состоящем из различных деталей с раз­личными законами распределения. Кроме того, еще до монтажа оборудование подвергается приработке, причем различное оборудование к моменту ввода в эксплуатацию нарабатывает различное количество часов (на заводских стендах). Все это приводит к тому приводит к тому, что поток устанавливается значительно быстрее, чем в случае суммы потоков одинаковых элементов.   

Как следует из предельных теорем, если вероятность отказа каждого элемента мала и отказы независимы, то при числе элементов m ® 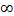 суммарный поток отказов стремится к пуассоновскому, т. е. не имеет не имеет последействия. Если к тому же каждый поток стационарен, то суммарный поток тоже стационарен, т.е. является простейшим независимо от вида закона распределения наработок между отказами.

Точность приближения суммарного потока отказов к модели простейшего потока зависит от числа элементов  m  отличия законов распределения времени безотказной работы отдельных элементов от экспоненциального и ожидаемого числа отказов [2, 5, 10, 23].

 Если наработки между отказами подчиняются экспоненциальному закону распределения, то поток отказов каждого элемента простейший.  Простейшим будет и суммарный поток отказов таких элементов, независимо от их числа.   

Если основная причина отличия закона распределения времени безотказной  работы элемента от экспоненциального заключается в наличии периода приработки, то, как показывает анализ, для того, чтобы отличие индивидуальных законов распределения мало влияло на  форму потока в случае внезапных отказов, необходимо выполнение  соотношения [ 10 ]

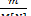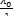>10 ( -1) при М [ N ] > 1.     (4.5)

М [ N ] -  математическое ожидание числа отказов на рассмат­риваемом отрезке времени;

 l _o = l (0) - значение интенсивности отказов в начальный момент времени;

l - установившееся значение интенсивности отказов.

Смысл приведенного неравенства заключается в том, что при больших значениях отношения m /M[N]  число отказов каждого элемента в общем потоке невелико и поэтому индивидуальные законы распределения элементов не влияют на закон распределения числа отказов в суммарном потоке. И наоборот, при малых значениях отношения m /M[N] от каждого элемента может быть получено   несколько отказов и закон распределения числа отказов суммарного пока будет в значительной степени определяться индивидуальными законами распределения наработок между отказами элементов. Обычно для сокращения времени испытаний (длительности наблюдения на интервале времени t + _D t ) производят испытания не одного элемента, оборудования, сооружения и т. д., а группы объектов.  Очевидно, что все приведенные выше выводы  остаются в силе и в этом случае.  Отличия заключаются в следующем. Поток постепенных отказов элемента  или даже всей системы нельзя рассматривать как сумму потоков отказов большого числа элементов с малыми интенсивностями отказов, так как постепенные отказы обусловливаются в основном  одним или несколькими  элементами.

 При наличии большой группы элементов, можно рассматривать приближение суммарного потока постепенных отказов простейшим или неоднородным пуассоновским потоком. Законы рас­пределения наработок между отказами в случае постепенных отка­зов значительно отличаются от экспоненциального и условие бли­зости суммарного потока к простейшему задается в этом случае неравенством

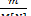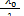>10 ( - 1) при М [ N ] > 1        (4.6)

где m — количество элементов, обусловливающих постепенные отказы.

Таким образом, при соблюдении неравенств (4.5) и (4.6) ос­новной причиной последействия в потоках отказов сложного оборудования являются случайные внешние воздействия.

Из сделанного обзора потоков отказов объектов водоснабжения видно, что часто принимаемая при расче­тах гипотеза о близости потока к простейшему недостаточно обос­нована и, во всяком случае, требует проверки.