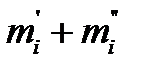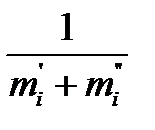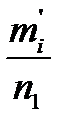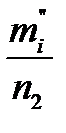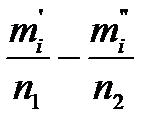Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Непараметрические гипотезы - это такие гипотезы, для про­верки которым не надо знать закон распределения случайной величины.

Чувствительность критериев используемых для проверка непараметрических гипотез, ниже, чем чувствительность критериев для проверки параметрических гипотез, так как закон распределения дает наиболее полную информацию о случайной величине.

В настоящее время применяются две группу, непараметрических критериев:

Первая группа - это группа гипотез, при проверке которых в качестве критериев используется статистики, основанные на раз­ности эмпирических и теоретических, распределений изучаемого приз­нака. В этом случае в качестве критериев используются:

критерий c² (Пирсона),

критерий L (Колмогорова),

критерий D_т (Смирнова),

критерий Реньи /(R - критерий),

критерий ω².

Эта группа критериев как правило, используется для проверки принадлежности рассматриваемой выборочной совокупности к некоторой генеральной совокупности;

Вторая группа - при проверке гипотез этой группы используется критерии, основанные на простейших функциях ранговых статистик

(используются свойства вариационных рядов).

К этим критериям. относятся:

критерий знаков,    

критерий серий,

критерий Вилкоксона

критерий Ван дер Вардена ( X —критерий).

Они используется для проверки однородности двух выборочных совокупностей. При этой распределение признаке случайных величин должно быть непрерывным.

1. Проверка однородности двух выборочных наблюдений с помощью c² - критерия.

Пусть n₁ и n₂ - объемы выборочных наблюдений. Разбиваем число наблюдений в каждой выборке на    l    интервалов. В каждый  интервал попадает какое-то количество  наблюдений m _i , т.е.:

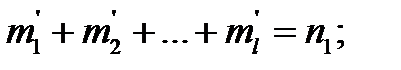
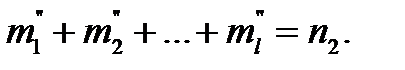
Далее вычисляем значение c²  - критерия до формуле:

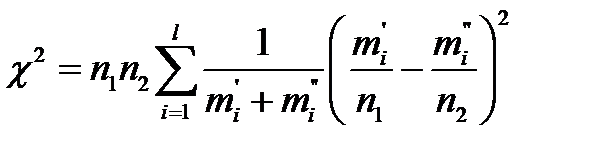(5.37)

Полученное значение x² сравнивается с теоретическим, т.е.

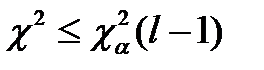
где   l  - количество интервалов.

Если 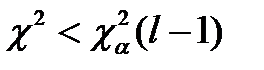, то гипотеза об однородности наблюдений принимается. Это - наиболее часто применяемый критерий при проверке непараметрических гипотез, когда  n₁  и  n₂  достаточно велики. Чем больше n , тем чувствительнее этот критерий.

Пример:  От разных заводов поступили две трубы. Из труб вырезаны образцы и определены значения s _в .

Проверить, являются ли обе трубы однородными в отношении значении характеристики s _в

Данные наблюдений и подсчет значения критерая приведены в таблица 5.2.

Таблица 5.2

Интервалы изменения s в	Частоты							(5)х(6)
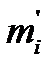
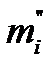
1	2	3	4	5	6	7	8	9
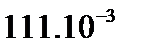
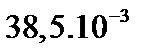
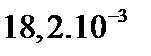
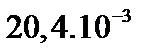
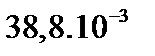
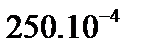
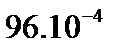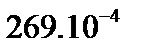
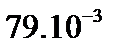
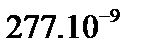
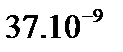До 42 42-45 45-48 48-51 Более 51	9 13 20 12 3	- 13 35 37 14	9 26 55 49 17		0,158 0,228 0,351 0,210 0,053	- 0,130 0,354 0,374 0,142	0	0
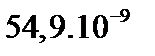
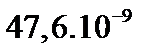
суммы	57	99	15,6		1,000	1,000		417,10

Из таблицы видно, что вторая выборка сдвинута относительно первой.

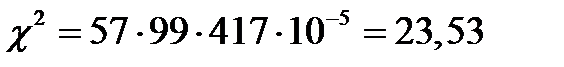
Пусть α = 0,05, тогда при числе степеней свободы l - 1 = 5 - 1 = 4 значение 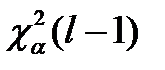 составит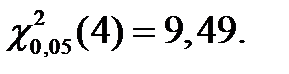

Следовательно,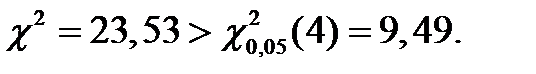

Таким образом, гипотеза об однородности двух труб ( в отношений значений средней величины ) должна быть отвергнута,

2.Проверка однородности двух выборочных наблюдений с использованием критерия Вилкоксона

Этот критерий применяются, когда объема выборок малы.

а)  Проверка гипотез путем вычисления значения критерия, основанного на числе инверсий u.

Пусть имеем два выборочных наблюдения объемами n₁ и n₂.

Все элементы обеих выборок выписываются в два вариационных ряда:

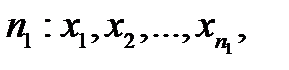
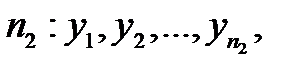
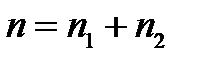 -суммарное количество наблюдений.

Далее все наблюдения выписываются в одну возрастающую после­довательность (в один вариационный ряд), т.е.

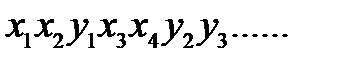
Затем вычисляется число инверсий   u   для    x   или   y.

Например, подсчитаем число инверсий 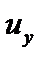   для  y .

Напомним , что под инверсией   y  понимается число, ровное коли­честву элементов  x, предшествующих рассматриваемому эле­менту    y  , т,е.

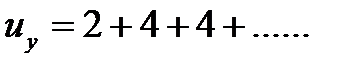
При этом среднее число инверсий (оценка, математического ожидания) равно:

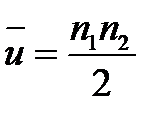                      (5.38)

Дисперсий числа инверсий равна:

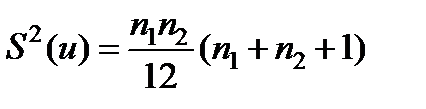           (5.39)

В том случае, если    n₁  и    n₂ > 10, то распределение случайного значения числа инверсий вариационного ряда асимптотически нормально. Это свойство используется для построения критической области статистики   u .  Поскольку в этом случае (нормального распределе­ния) функций распределения числа инверсий симметрична, то при про­верке гипотезы об однородности используется двухсторонний крите­рий (рис. 5.1), т.е.

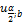
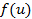
u

Рис. 5.6

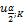
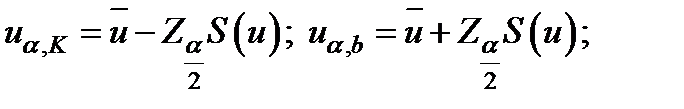       (5.40)

Следовательно, если 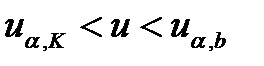, то гипотеза об одно­родности выборочных наблюдений должна быть принята.

В случае, ес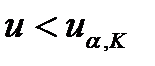ли  или 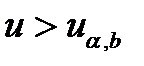 - гипотеза об однороднос­ти выборочных наблюдений должна быть отвергнута.

Пример

Проводились наблюдения над двумя группами  гидравлических машин, эксплуатируемых в различных климатических зонах. В результате проведенных наблюде­ний зафиксировано число отказов n₁ и n₂, Времена между отка­зами  составили t _j     и S _j , соответственно:          

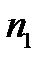 = 23; 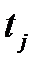 = 40, 60, 65, 75, 80, 90, 95, 101, 110, 115, 124, 135, 151, 155, 160, 167, 176, 180, 195, 205, 220, 268, 280,

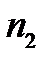= 22; S _j = 23, 78, 96, 104, 122, 137, 165, 171, 192, 203, 221, 226, 231, 245, 252, 263, 270, 278,  252, 298, 305, 340.

Проворить однородность условий эксплуатации двух групп машин.

По этим наблюдениям составляем один вариационный ряд:

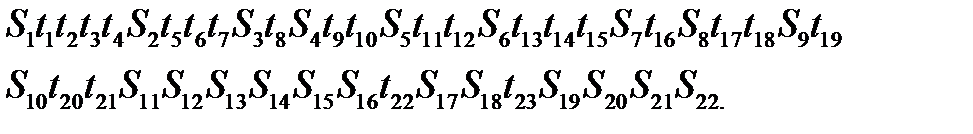
Вычисляем число инверсий для t

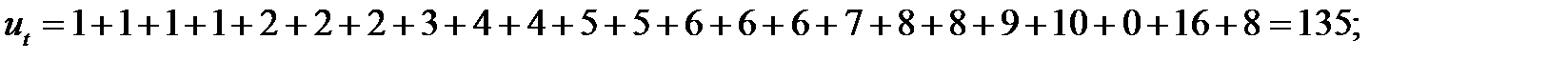
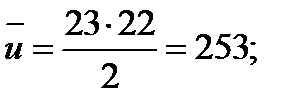
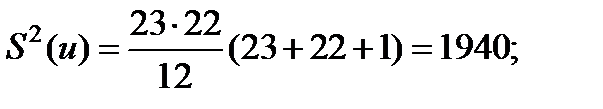
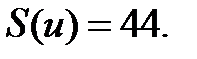
При уровне значимости α = 0,05 для нормального распреде­ления:

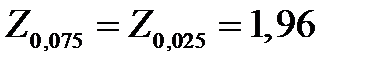
Тогда: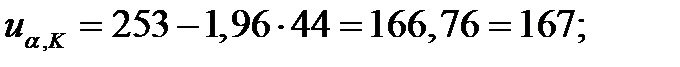

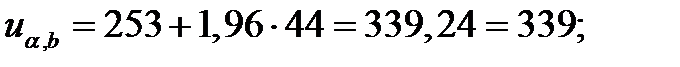
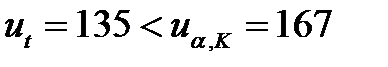 т.е. число инверсий попадает в критическую зону. Следовательно, гипотеза об однородности условий эксплуатации машин должна быть отвергнута.

При использовании критерия Вилкоксона в качестве сравнивае­мых характеристик наблюдений используются средние значения выбо­рочно наблюдений ( в данной примере они смещены друг относительно друга).

б) Проверка гипотезы однородности выборочных наблюдений основывается на вычислении ранговой W - статистики.

Под рангом вариационного ряда понимается порядковый номер элемента вариационного ряда. Пусть имеем вариационный ряд:

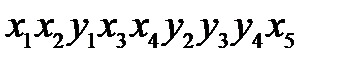
Тогда ранги элементов будут: 1 2 3 4 5 6 7 .....

По общему вариационному ряду ( для обеих выборок) вычисляется W – статистика для той выборки, в которой число элементов меньше

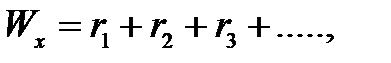
       где 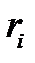- ранг i –го элемента в выборке меньшего объема, пример, .

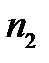Среднее значение (математическое ожидание) W - статистики равно:

       (5.41)

Дисперсия W - статистики:

       (5.42)

Порядок проверки гипотезы об однородности наблюдений с использованием W - статистики сводится к следующему.

По статистическим данным строится общий вариационный ряд и вычисляется W - статистика для элементов выборки меньшего объема. Полученное значение W - статистика сравнивается с ее критическими значениями: ω(α;m;n) и W(α;m;n), т.е.

ω(α;m;n)< W < W(α;m;n)              (5.43)

При соблюдении указанного неравенства гипотеза со однородности выборок принимается . При этом ω(α;m;n) определяется по таблице 17 приложения 2  для W - статистики, а

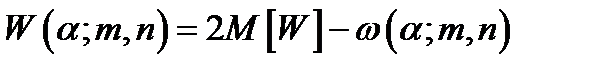                  (5.44)

Эта формуле справедлива для  m   и  n  > 25.

Если  m  и  n < 25, то :        

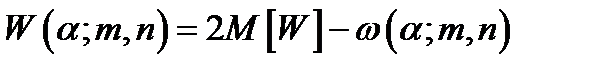            (5.45)

и 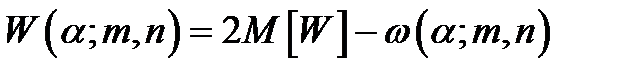 начиная с  m  и  n  >5.

Пример. (используется данные предущего примера)

Вариационный ряд:

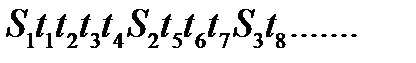
Ранги вариационного ряде: 1 2 3 4 5 6 7 8 9 10 11..;

Значение W -       - статистики: ,

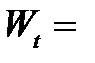2+ 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 13 + 14 + 16 + 17 + 19 + 20 + 21 + 23 +25 + 26 + 28 + 30 + 31 + 38 + 41 = 401 .

Математическое ожидание:

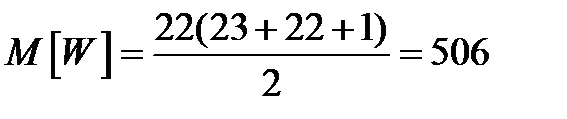
Дисперсия:

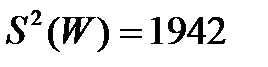, следовательно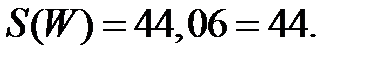

По таблице 17  приложения 2 для W - статистики , находим:

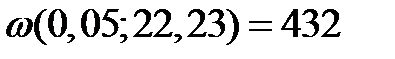
W (0,05; 22, 23) = 2M[W] - 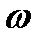(0,05; 22; 23) = 2 ·506 - 432 = 580.

Таким образом , W_t = 401  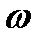<  (0,05; 22,23) = 432.

Следовательно, гипотеза об однородности выборочных наблюдений отвергается.

с). Проверка гипотез об однородности двух выборочных наблюдений с использованием критерия знаков

Критерий знаков используется в той случае, если объемы наблюдений в выборках одинаковы, т.е. n₁ = n₂ = n . В этом случае проверяется гипотеза о равенстве математических ожиданий в рассматриваемых выборках .

Метод проверки гипотез, основан на вычислении числа положительных ( отрицательных) разностей  μ  результатов наблюдений и сопоставлений полученного значения с критический значением критерия   m (α;n), соответствующего уровню значимости  α  и числу наблюдений  n.

Для определения числа положительных разностей  μ  результаты двух групп наблюдений выписываются в ряд в соответствий с оче­редностью их получения и сравниваются друг с другом.

Величина  μ  является случайной величиной, подчиняющейся биномиальному распределению с параметрами n  и p= 0,5, т.е.

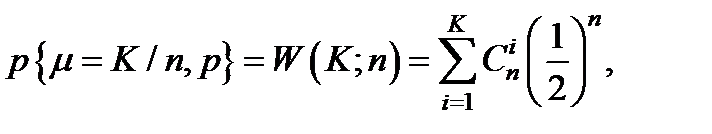           (5.46)

где k = 0,1,2,……..,n

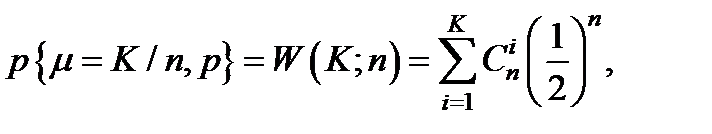(5.47)

В случае, если средние значения двух выборочных наблюдений равны, то вероятность получения положительных и отрицательных раз­ностей равны, т.е. Р = 0,5. В качестве альтернативных гипотез Н₁ в случае использования одностороннего критерия , могут быть:

1) Н{Р < 0,5}, тогда нулевой гипотеза Н_о принимается, если

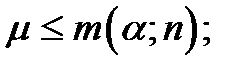                                  (5.48)

2) Н{p > 0,50},  тогда

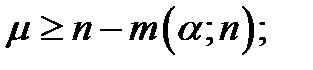                            (5.49)

В случае использования двухстороннего критерия:

3/) Н{Р ≠ 0,5} и нулевая гипотеза принимается, если

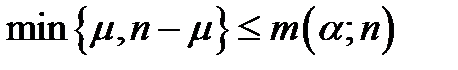             (5.50)

Значение критерия  m (α ; n)  определяется из таблицы 16 приложения 2  по принятому значению   α   к объему выборочных наблюдений  n.

Часто при проварке гипотез с использованием критерия знаков определяется не критическое значение числа положительных разностей  m (α ; n),  а минимально необходимое число наблюдений, cоответствующее m(α;n)=μ,  при котором нулевая гипотеза Н_о может быть принята, если по результатам наблюдений получено число положительных разностей μ.

Критическое значение число наблюдений N(α;μ) опреде­ляется из соотношения:

N(α;μ) = min{n}

                  m(α;n) = μ                                   (5.51)

В этом случае условиями принятия нулевой гипотенузы. являются:

1/ 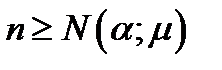                             для 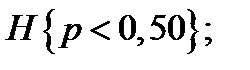                              (5.52)

2/ 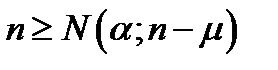                        для 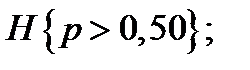                              (5.53)

3/ 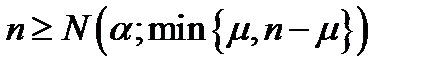         для 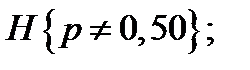                              (5.54)

Применение этого критерия рассмотрим на следующем примере. При эксплуатации двух однотипных насосных  агрегатов  проводились наблюдения за наработками до получения 16 отказов. Данное наблюдения приведены в табл. 5.3.

Таблица 5.3

 

Номера отказов	1	2	3	4	5	6	7
Нас.  агр. № 1	50	98	120	175	198	260	340
Нас. агр. № 2	30	80	150	190	210	250	310
Знак разности	+	+	-	-	-	+	+

 

8	9	10	11	12	13	14	15	16
410	480	560	610	630	670	750	810	880
390	490	580	620	670	690	740	820	900
+	-	-	-	-	-	+	-	-

Следовательно: n =16, µ = 6. Проверяем гипотезу о равенстве характеристик надежности двух насосных агрегатов  при α = 0,05. В качестве альтернативной гипотезы Н₁ принимаем гипотезу Н{Р<0,5}, т е., что насосный агрегат № I является менее надежной.

По таблице 16 приложения 2  при  n = 16 и α = 0,05, находим:

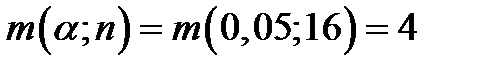 и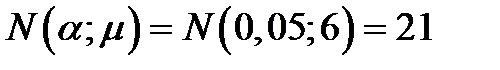

Таким образом μ = 6 > m (0,05;16) = 4  и   n = 16 < N (0,05;7) = 21. Неравенства (5.48) и (5.52)  не удовлетворяется и гипоте­за о равенство показателей надежности рассматриваемых насосных агрегатов  должна быть отвергнута.

ГЛАВА 6. ПРИМЕРЫ ОЦЕНКИ НАДЕЖНОСТИ ВОДОПРОВОДНЫХ СООРУЖЕНИЙ