Случай последовательного соединения элементов самый частый, который встречается в водопроводных системах: трубопроводы , оборудование водозаборных , очистных сооружений и т.д.
1. Мгновенное восстановление.
Пусть система состоит из n элементов, 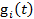 - функция распределения времени жизни i-го элемента, tі - среднее время безотказной работы i-го элемента. Элементы отказывают независимо друг от друга. В момент отказа элемента он мгновенно и полностью восстанавливается (например, происходит замена новым идентичным элементом). Поток отказов элемента будет, очевидно, процессом восстановления, а поток отказов системы, поскольку каждый отказ элемента есть отказ системы, будет суммой n независимых процессов восстановления. Для такой системы можно в принципе рассчитать все характеристики надежности.
- функция распределения времени жизни i-го элемента, tі - среднее время безотказной работы i-го элемента. Элементы отказывают независимо друг от друга. В момент отказа элемента он мгновенно и полностью восстанавливается (например, происходит замена новым идентичным элементом). Поток отказов элемента будет, очевидно, процессом восстановления, а поток отказов системы, поскольку каждый отказ элемента есть отказ системы, будет суммой n независимых процессов восстановления. Для такой системы можно в принципе рассчитать все характеристики надежности.
Обозначим 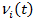 - случайное число отказов i-го элемента на [0, t ] ,
- случайное число отказов i-го элемента на [0, t ] , 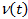 - число отказов системы на [0, t ].
- число отказов системы на [0, t ].
Тогда,  (3.69)
(3.69)
Так как распределение 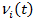 - известно, то возможно просчитать распределение
- известно, то возможно просчитать распределение 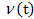 . Обозначим
. Обозначим 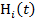 и
и 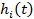 - функция восстановления и плотность восстановления потока отказов i-го элемента, Н (t) - среднее число отказов системы на [0, t ],
- функция восстановления и плотность восстановления потока отказов i-го элемента, Н (t) - среднее число отказов системы на [0, t ], 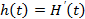 - интенсивность отказов системы. Тогда из (3.69) следует, что
- интенсивность отказов системы. Тогда из (3.69) следует, что

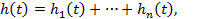 (3.70)
(3.70)
В принципе можно найти распределение остаточного времени (время от момента t до ближайшего отказа системы). Не будем заниматься выводом громоздких формул для распределений 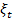 и
и 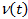 - на практике их почти не используют.
- на практике их почти не используют.
Рассмотрим работу системы в стационарном режиме. При известных условиях
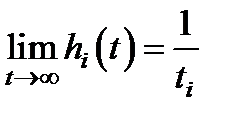 , откуда следует,
, откуда следует,
что 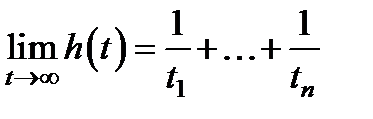
C другой стороны, для любого стационарного потока интенсивность потока обратна к среднему интервалу между соседними точками потока. Отсюда среднее время между соседними отказами (или средняя наработка на отказ) Т равно
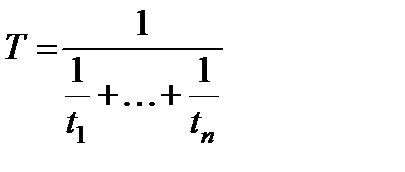 (3.71)
(3.71)
Далее пусть 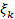 - стационарное остаточное время жизни k -го элемента, x- стационарное остаточное время жизни системы. Поскольку
- стационарное остаточное время жизни k -го элемента, x- стационарное остаточное время жизни системы. Поскольку
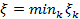 , то :
, то :
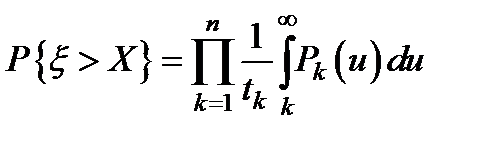 , 3.72)
, 3.72)
где 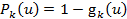 - функция надежности k -го элемента.
- функция надежности k -го элемента.
Пусть t - случайное время между соседними отказами системы (следует, иметь в виду, что последовательные интервалы между отказами системы зависимы) и
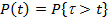 .
.
Из теории стационарных потоков [23] следует, что
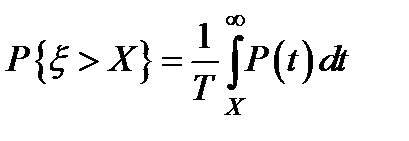 .
.
Приравнивая этот интеграл к правой части (3.72) и дифференцируя по Х получим:
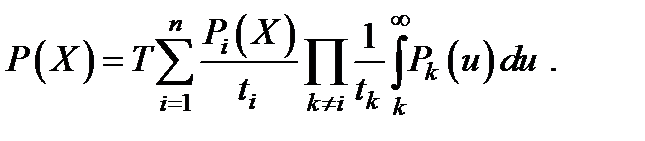 (3.73)
(3.73)
2. Случай большого числа элементов в системе.
Григелионис доказал [23], что при выполнении некоторых общих условий сумма большого числа независимых потоков асимптотически будет пуассоновским потоком с переменным параметром. Пуассоновским потоком с переменным параметром λ(t) называется точечный поток, который определяется двумя условиями:
а) появления точек потока на непересекающихся интервалах независимы;
б) вероятность появления k точек на интервале равна:
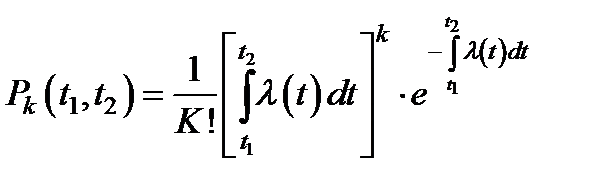 (3.74)
(3.74)
Не приводя точной формулировки теоремы Григелиониса отметим, что главное условие этой теоремы состоит в том, что интенсивность каждого из слагаемых потоков бесконечно мала по отношению к интенсивности суммарного потока, то есть применительно к нашему случаю интенсивность потока отказов каждого элемента должна быть мала по сравнению с интенсивностью потока отказов системы
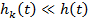 .
.
Итак, предположим, что число элементов n велико и выполнены условия теоремы Григелиониса. Тогда поток отказов системы можно считать с хорошим приближением пуассоновским потоком с переменным параметром. Из (3.74) получаем, что среднее число отказов системы на [0,t] равно:
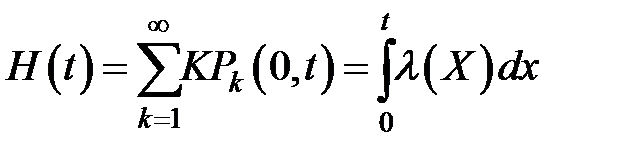
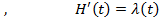 ,
,
то есть параметром пуассоновского потока будет введенная раньше интенсивность потока 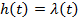 .
.
Для сложных систем интенсивность h(t) меняется медленно и на интервале между соседними отказами ее можно считать постоянной. Этот факт связан с тем, что в сложной ( n - велико) и относительно надежной системе время жизни каждого отдельного элемента очень велико, гораздо больше интересующего нас интервала времени. Естественно, поэтому, что плотности отказов 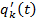 меняются на этом интервале медленно, а с ними так же медленно меняются
меняются на этом интервале медленно, а с ними так же медленно меняются 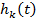 и
и 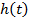 . Для каждого элемента поток восстановлений будет приближенно стационарным только через время, равное нескольким средним временам жизни. По этим же причинам можно интенсивность потока h (t) рассчитывать по приближенной формуле :
. Для каждого элемента поток восстановлений будет приближенно стационарным только через время, равное нескольким средним временам жизни. По этим же причинам можно интенсивность потока h (t) рассчитывать по приближенной формуле :
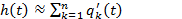 (3.75)
(3.75)
Если h(t) меняется медленно, то остаточное время жизни 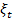 имеет распределение:
имеет распределение:
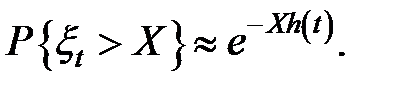 (3.76)
(3.76)
Вероятность появления на участке (t, t+x) k отказов можно считать по приближенной формуле
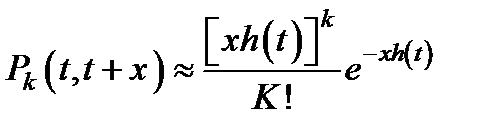 (3.77)
(3.77)
Распределение интервала между соседними отказами, если этот интервал начался в момент t можно считать по формуле (3.76) .
3. Конечное время восстановления
Представим, что время жизни k -го элемента имеет функцию распределения 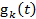 и среднее
и среднее 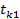 , а время восстановления имеет функцию распределения
, а время восстановления имеет функцию распределения 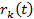 и среднее
и среднее  . Рассматривается случай, когда при отказе элемента вся система останавливается и включается в работу в момент окончания восстановления. Естественно также предположить,что во время восстановлений система "застывает", то есть надежность элементов в это время не меняется.
. Рассматривается случай, когда при отказе элемента вся система останавливается и включается в работу в момент окончания восстановления. Естественно также предположить,что во время восстановлений система "застывает", то есть надежность элементов в это время не меняется.
Работа системы может быть изображена так (см. рис.3.9 ):
| 0 |
Рис. 3.9. Интерпретация работы и восстановления системы
Прямоугольники соответствуют участкам восстановлений. Если вырезать эти участки и сомкнуть интервалы работы, то получим поток, рассмотренный в предыдущем пункте. Это соображение дает возможность вычислить все характеристики надежности. Но, как и выше, ограничимся тем, что найдем стационарные характеристики, а затем рассмотрим случай большого числа элементов.
Пусть То - среднее время безотказной работы системы, а Тв= t среднее время восстановления систем. Из сказанного выше очевидно, что
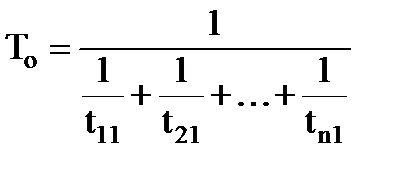 , (3.78)
, (3.78)
а функция распределения времени жизни выражается из (3.73).
Если в стационарном режиме произошел отказ системы, то с вероятностью
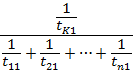
это отказ k -го элемента. Поэтому функция распределения времени восстановления системы равна:
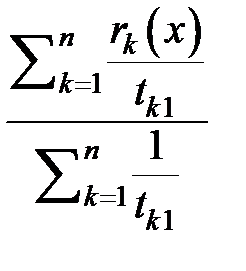 , (3.79)
, (3.79)
а среднее время
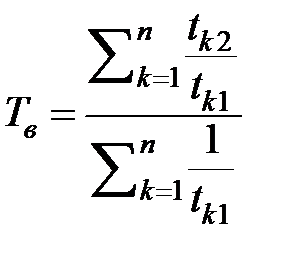 . (3.80)
. (3.80)
Отсюда стационарный коэффициент готовности
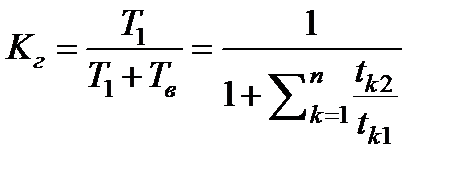 (3.81)
(3.81)
Чтобы получить распределение остаточного времени жизни системы x , надо правую часть (3.73) умножить на коэффициент готовности:
 , (3.82)
, (3.82)
Перейдем теперь к случаю, когда система состоит из большого числа элементов. Если бы восстановление было мгновенным, то поток отказов системы был пуассоновским потоком с переменным параметром. Наш поток (см. рис. 7) получится, если мы разрежем пуассоновский поток в точках отказа и вставим туда интервалы восстановления. При этом, если на оси первого потока в момент t (t - наработка системы) возник отказ, то с вероятностью
p k (t) = 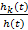
это отказ k -го элемента.
Поэтому, если в момент, когда наработка системы достигла величины t, возник отказ, то функция распределения времени восстановления ht будет равна:
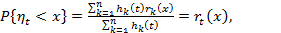 (3.83)
(3.83)
а среднее время восстановления
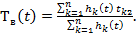 (3.84)
(3.84)
Для оценки других характеристик предположим дополнительно, что время восстановления мало по сравнению с интервалом безотказной работы системы (это предположение естественно - система почти все время должна работать). Тогда можно пренебречь разницей между календарным временем и наработкой системы. Найдем нестационарный коэффициент готовности системы
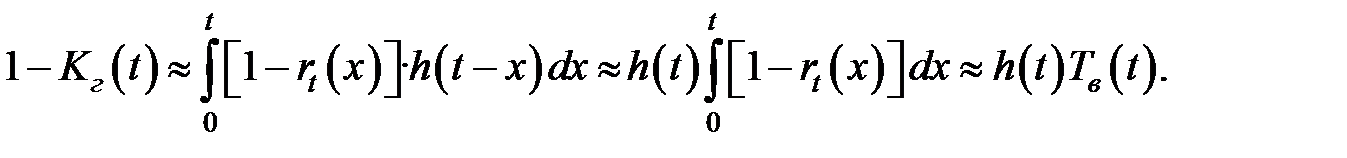 (3.85)
(3.85)
Из (3.85) найдем среднее время, которое на [0,t] система находится в неисправном состоянии, обозначим его 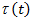 . Если рассмотреть единичный процесс
. Если рассмотреть единичный процесс
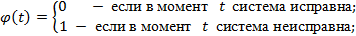
то 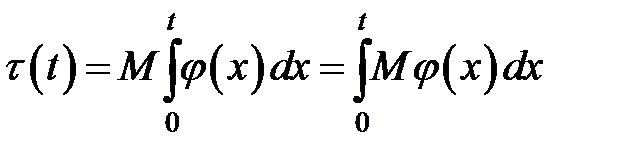
Но 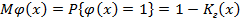 ,
,
отсюда
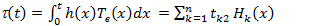 (3.86)
(3.86)
Если h (t) меняется медленно, тогда остаточное время жизни системы 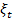 имеет, распределение [см. (3.76)].
имеет, распределение [см. (3.76)].
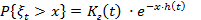 (3.87)
(3.87)
4. Конечное время восстановления (независимое восстановление) .
Рассмотрим случай (см. рис. 3.10 ), когда каждый элемент работает, отказывает, восстанавливается, снова работает и так далее, независимо от других элементов. Время жизни k-го элемента имеет функцию распределения 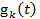 , а время ремонта -
, а время ремонта - 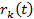 . Соответственно,
. Соответственно, 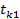 и
и  среднее время жизни и восстановления.
среднее время жизни и восстановления.
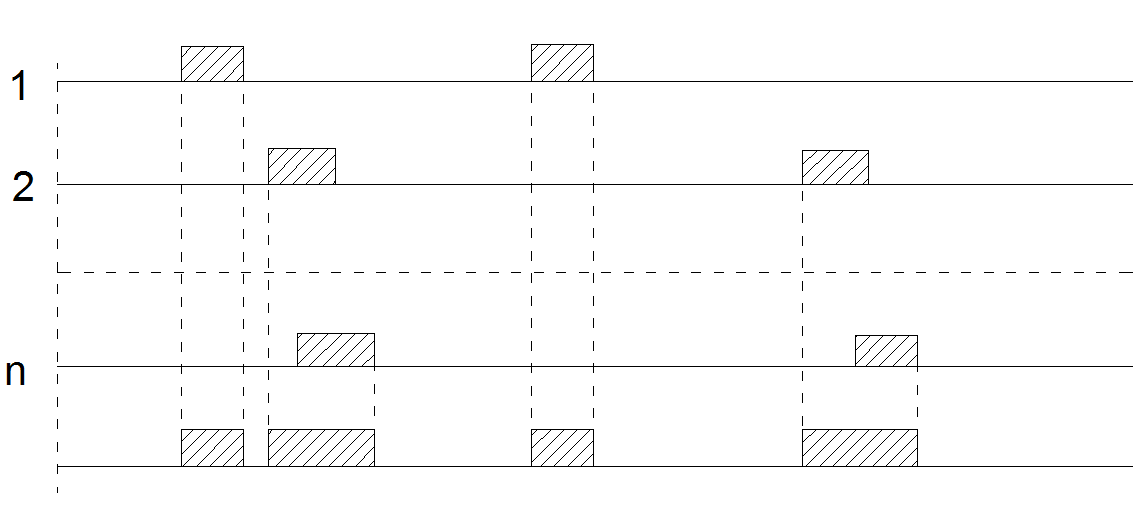
Рис.3.10. Интерпретация работы и восстановления системы из n элементов
На первых n осях времени изображена работа элементов, на последней оси - работа системы. Прямоугольниками отмечены участки восстановления. Пусть То - среднее время безотказной работы, а Тв среднее время восстановления системы в стационарном режиме. Рассмариваемый процесс H(t) имеет стационарное распределение и стационарную вероятность

Допустим интенсивность потока отказов системы в стационарном режиме λ.
Тогда:
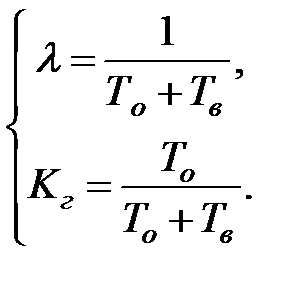 (3.88)
(3.88)
Из (3.88) можно найти Tо и Tв . Поскольку элементы в системе работают независимо, то ее коэффициент готовности
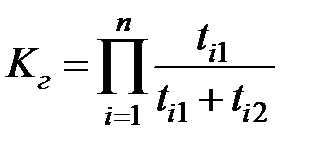 (3.89)
(3.89)
Аналогично оценим интенсивность потока отказов системы L. Для того, чтобы на [t, t+dt] произошел отказ системы надо, чтобы в момент t все элементы, кроме одного, скажем k -го, были исправны, вероятность этого
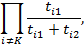
a k-тый элемент на [ t, t+dt] отказал, вероятность этого 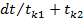 . Перемножая эти две величины и суммируя по k , получим, что вероятность отказа системы на
. Перемножая эти две величины и суммируя по k , получим, что вероятность отказа системы на
[ t, t+d] равна:
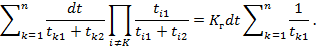
С другой стороны, по определению интенсивности L эта вероятность равна Ldt и отсюда:
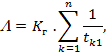
Используя теперь формулу (3.88) , получаем:
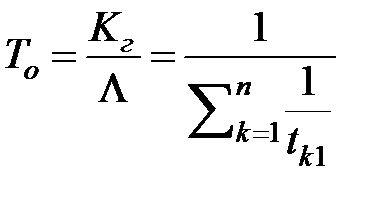 ,
, 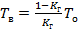 . (3.90)
. (3.90)
 .4.6. Марковские методы
.4.6. Марковские методы
1 . Точные формулы для характеристик марковского процесса. Предположим, что процесс H ( t ) описывающий работу системы - марковский однородный процесс с конечным числом состояний, обозначим состояния - 0,1,2... n. Состояния {0,1,2,…, m -1} = E + соответствуют исправным состояниям системы, а состояния {m,...,n}=E - - неисправным состояниям системы. Процесс H(t) называется марковским однородным процессом, если для любых состояний 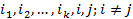 и любых моментов
и любых моментов 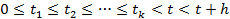 условная вероятность
условная вероятность
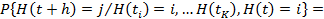
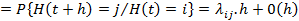 , при
, при 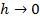 . (3.91)
. (3.91)
Из этого определения следует, что вероятности будущих состояний процесса определяются знанием его настоящего состояния и при этом условии не зависят от прошлого поведения процесса. Если, например, в системе время безотказной работы каждого элемента и время его восстановления имеют экспоненциальное распределение, то процесс, описывающий поведение такой системы, будет марковским однородным процессом. Однако, эти свойства могут иметь процессы и в гораздо более общих ситуациях, например, когда отказы элементов зависимы, а время восстановления элементов зависит от состояния системы. В настоящее время нет необходимости описывать все те случаи, когда возникает марковский процесс. Проще для каждой конкретной системы проверять условие (3.91). Исходя из определения, легко показать [23 ] , что в каждом состоянии i процесс H(t) находится в течение экспоненциального времени 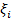 (см. рис. 3.11) с параметром -
(см. рис. 3.11) с параметром - 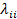 .
.
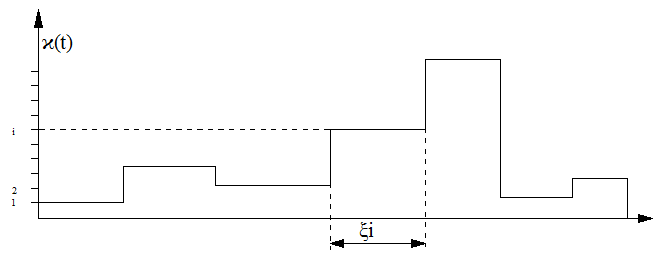
Рис.3.11. Интерпретация процесса безотказной работы и восстановления системы с экспоненциальным распределением
Т.е. 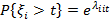 ,
,
где 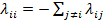 .
.
Вероятность того, что процесс из состояния i прейдет в состояние j равна
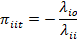
(если λii=0, то состояние i будет поглощающим, так как, попав в него, процесс навсегда в нем остается; в этом случае можно положить 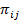 =0). Таким образом, марковский однородный процесс в каждом состоянии находится экспоненциально распределенное время, и эти времена независимы, а переход из состояния в состояние управляется цепью Маркова с переходными вероятностями
=0). Таким образом, марковский однородный процесс в каждом состоянии находится экспоненциально распределенное время, и эти времена независимы, а переход из состояния в состояние управляется цепью Маркова с переходными вероятностями 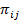 . Такая трактовка марковского процесса оказывается для ряда задач удобной.
. Такая трактовка марковского процесса оказывается для ряда задач удобной.
Пусть: 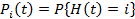
Вероятность состояний 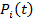 удовлетворяют уравнениям Колмогорова
удовлетворяют уравнениям Колмогорова
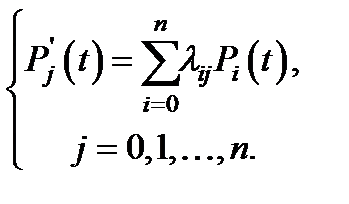 (3.92)
(3.92)
Эту систему можно записать и в матричной форме:
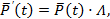
где 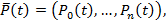 - вектор вероятностей состояний, а
- вектор вероятностей состояний, а 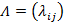 - матрица интенсивностей перехода.
- матрица интенсивностей перехода.
Эта матрица характеризуется двумя свойствами:
a) все 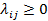 при
при 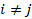 ;
;
б) 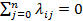
Для того, чтобы системе (3.92) имела единственное решение, то есть процесс H(t) был однозначно определен, надо задать начальное распределение процесса 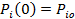 .
.
Систему (3.92) можно решить, применив к ней преобразование Лапласа. Пусть
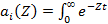 .
.
Тогда, используя элементарные свойства преобразования Лапласа получим:
. 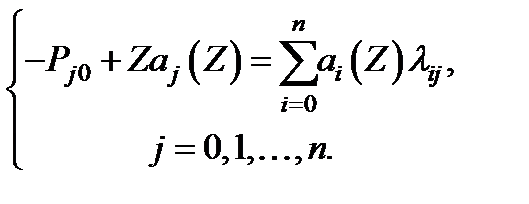
Решение этой системы по правилу Крамера дает [23 ]
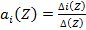 , (3.93)
, (3.93)
где 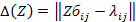
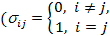 - символ Кронекера) ,
- символ Кронекера) ,
а определитель 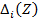 получается из определителя
получается из определителя 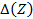 заменой i-той строки определителя строкой начальных вероятностей
заменой i-той строки определителя строкой начальных вероятностей 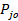 . Здесь
. Здесь 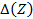 есть многочлен степени (n + 1), a
есть многочлен степени (n + 1), a 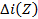 - многочлен меньшей степени. Отсюда, по формуле обращения (23), находятся сами вероятности
- многочлен меньшей степени. Отсюда, по формуле обращения (23), находятся сами вероятности 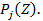 Конечно, при большом числе состояний здесь могут возникнуть непреодолимые вычислительные трудности. Возможно применение ЭВМ при этом.
Конечно, при большом числе состояний здесь могут возникнуть непреодолимые вычислительные трудности. Возможно применение ЭВМ при этом.
Предположим теперь, что состояния образуют один эргодический класс. Это значит, что для любых i и j найдутся
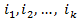 такие,
такие,
что 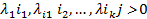 ,
,
то есть из любого состояния i можно перейти в любое другое состояние j . Тогда существуют пределы 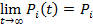 , не зависящие от начального распределения. Эти предельные величины, называемые стационарными вероятностями, удовлетворяют системе алгебраических уравнений:
, не зависящие от начального распределения. Эти предельные величины, называемые стационарными вероятностями, удовлетворяют системе алгебраических уравнений:
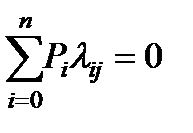 , (3.94)
, (3.94)
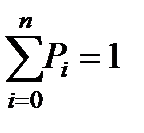 ,
, 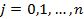
После этого краткого описания основных определений и фактов для марковских процессов приступим к подробному выводу характеристик марковских процессов, тех характеристик, которые в моделях теории надежности являются основными характеристиками надежности.
Пусть А - некоторое множество состояний, 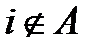 и
и 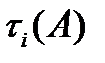
есть время перехода из состояния i в множество A то есть:
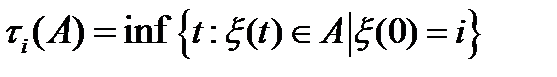 .
.
Распределение 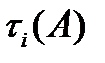 проще всего найти в терминах преобразования Лапласа. Поэтому обозначим:
проще всего найти в терминах преобразования Лапласа. Поэтому обозначим:
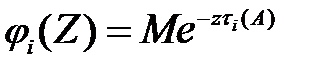 .
.
Тогда по формуле полных вероятностей для математического ожидания имеем:
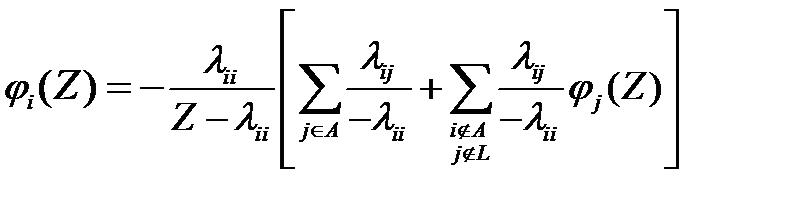
Это уравнение получается так: в состоянии i процесс проведет экспоненциальное время 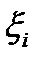 , его преобразование Лапласа. равно;
, его преобразование Лапласа. равно;
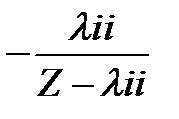 ,
,
а затем с вероятностью 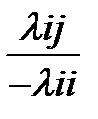
перейдет в состояние j . Если 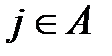 , то при этом условия
, то при этом условия 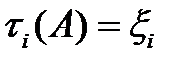 еcли же
еcли же 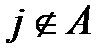 то
то 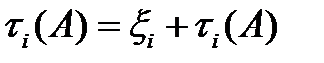 , причем эти слагаемые независимы. Преобразовав найденное уравнение, получим
, причем эти слагаемые независимы. Преобразовав найденное уравнение, получим
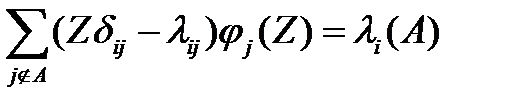 ,
,
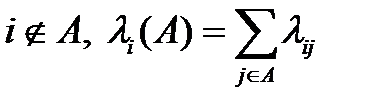 (3.95)
(3.95)
Решив систему, мы найдем 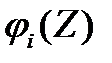 - это будет правильная рациональная дробь, обратив ее, мы найдем распределение величины
- это будет правильная рациональная дробь, обратив ее, мы найдем распределение величины 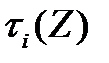 . Пусть
. Пусть
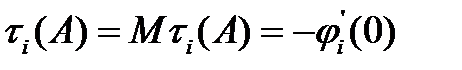 ,
,
Дифференцируя (3.95) по Z и полагая Z=0, получим для средних алгебраическую систему:
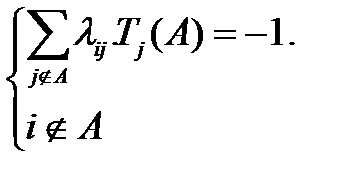 (3.96)
(3.96)
Пусть теперь 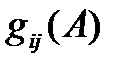 есть вероятность того, что мы попали в состояние
есть вероятность того, что мы попали в состояние 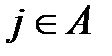 при условии, что в начальный момент мы находились в состоянии i и в первый раз попали в множество A . Нетрудно составить уравнения для этих вероятностей ;
при условии, что в начальный момент мы находились в состоянии i и в первый раз попали в множество A . Нетрудно составить уравнения для этих вероятностей ;
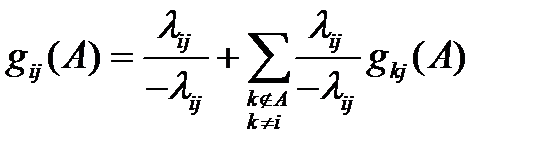 ,
,
которые получаются так: либо из i мы сразу попадем в j вероятность этого будет 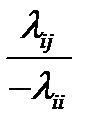 , либо из i с вероятностью
, либо из i с вероятностью 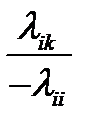 мы попадем в
мы попадем в 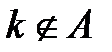 , при этом условии вероятность попасть в j будет равна
, при этом условии вероятность попасть в j будет равна 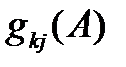 . Преобразуя уравнения, получим:
. Преобразуя уравнения, получим:
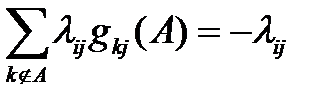 , (3.97)
, (3.97)
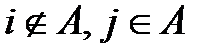
Из этой системы и находятся  . Покажем теперь, что через величины
. Покажем теперь, что через величины 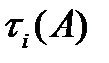 и вероятности
и вероятности 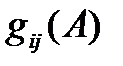 выражаются все введенные ранее (см. гл. 2) характеристики надежности
выражаются все введенные ранее (см. гл. 2) характеристики надежности 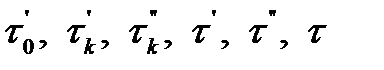 .
.
Пусть в начальный момент  , тогда
, тогда
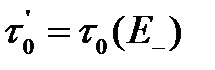 (3.98)
(3.98)
Кроме того, из (3.97) найдем 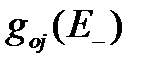 - вероятность того, что в момент первого отказа система попала в состояние
- вероятность того, что в момент первого отказа система попала в состояние 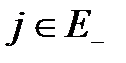 Но тогда по формуле полных вероятностей
Но тогда по формуле полных вероятностей
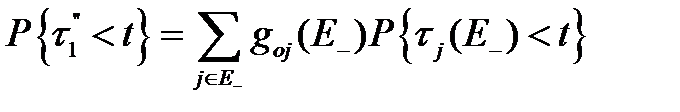 . (3.99)
. (3.99)
Вероятность того, что в момент первого восстановления система попадет в состояние 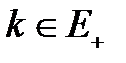 по формуле полных вероятностей равна:
по формуле полных вероятностей равна:
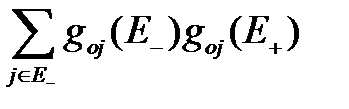 (3.100)
(3.100)
Зная эти вероятности, можно найти распределение 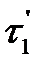 и вероятности состояний, в которые мы попадем в момент второго отказа и так далее. Мы не будем выписывать в общем случае распределений
и вероятности состояний, в которые мы попадем в момент второго отказа и так далее. Мы не будем выписывать в общем случае распределений 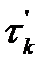 и
и 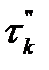 - это громоздко и, кроме того, на практике в основном используют стационарные величины -
- это громоздко и, кроме того, на практике в основном используют стационарные величины - 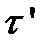 и
и 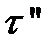 . Для того, чтобы найти их распределение, найдем предварительно такие вероятности:
. Для того, чтобы найти их распределение, найдем предварительно такие вероятности:
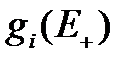 - вероятность того, что в момент восстановлен системы в стационарном режиме мы попали в состояние
- вероятность того, что в момент восстановлен системы в стационарном режиме мы попали в состояние  ;
;
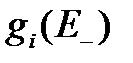 - соответственно, вероятность в момент отказа попасть в состояние
- соответственно, вероятность в момент отказа попасть в состояние 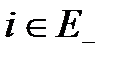 ,
,
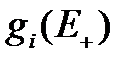 - есть вероятность за время dt перейти из
- есть вероятность за время dt перейти из 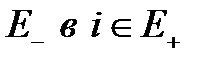 при условии, что за это время произошёл переход из
при условии, что за это время произошёл переход из 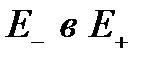 , то есть
, то есть
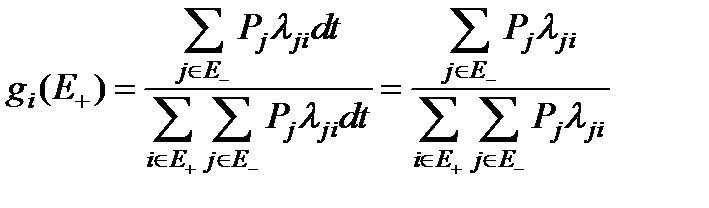 . (3.101)
. (3.101)
Аналогично
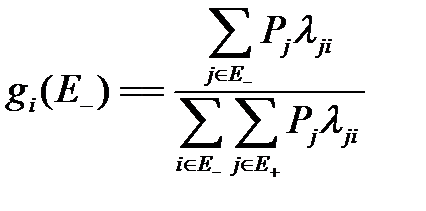 . (3.102)
. (3.102)
Здесь  - стационарные вероятности состояний, находимые из (3.94).
- стационарные вероятности состояний, находимые из (3.94).
Теперь:
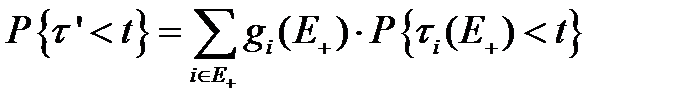 (3.103)
(3.103)
и
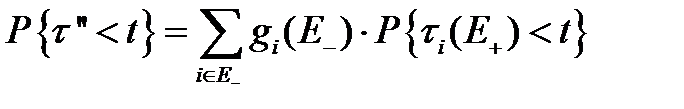
Распределение остаточного времени жизни системы t находится по формуле :
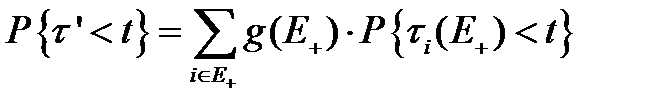 . (3.103)
. (3.103)
Еще проще находятся средние 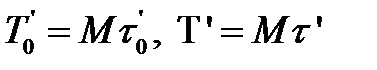
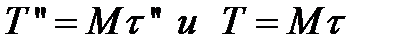
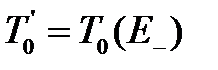 , (3.104)
, (3.104)
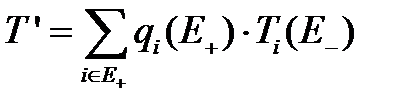 , (3.105)
, (3.105)
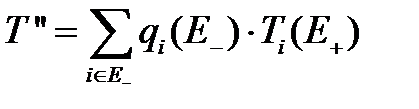 , (3.106)
, (3.106)
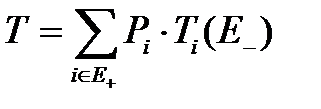 . (3.107)
. (3.107)
Наконец, коэффициент готовности
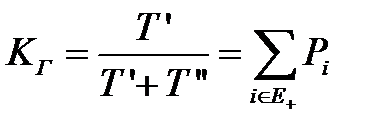 . (3.108)
. (3.108)
2. Процесс рождения и смерти.
Рассмотрим теперь один специальный марковский процесс, который очень часто возникает в моделях теории надежности (а также в теории массового обслуживания).
Процессом рождения и смерти (в литературе по теории надежности его также называют процесс гибели и размножения) называется марковский процесс с конечным или счетным числом состояний - 0,1,2,3,..., в котором мгновенные переходы возможны только в два соседних состояния, то есть:
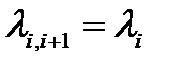 ,
, 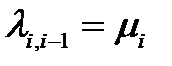 ,
,
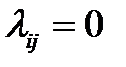 , если
, если 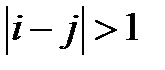 .
.
Кроме того, 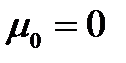 и, если число состояний конечно и равно
и, если число состояний конечно и равно 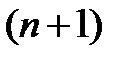 , то
, то 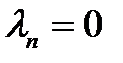 .
.
Для такого процесса уравнения Колмогорова имеют вид:
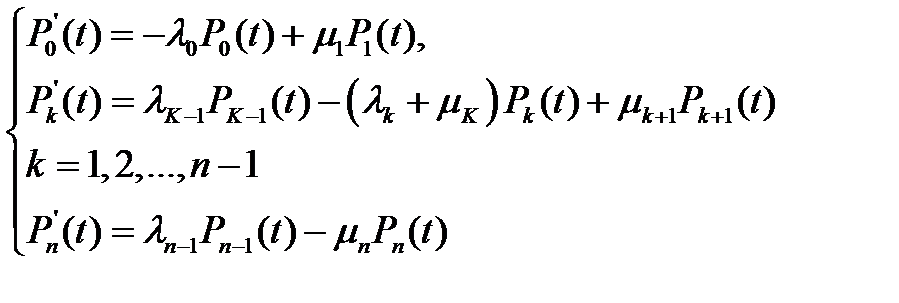 . (3.109)
. (3.109)
(для бесконечного числа состояний последнего уравнения не будет) .
Для того, чтобы процесс рождения и смерти имел стационарное распределение, необходимо и достаточно выполнение следующих условий [9] :
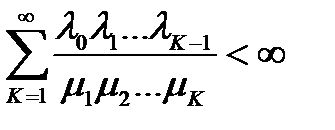 , (3.110)
, (3.110)
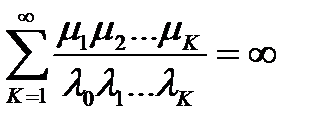 ,
,
(эти условия - для бесконечного числа состояний, для конечного числа состояний стационарные вероятности всегда существуют). Пусть выполнены условия (3.110), тогда стационарные вероятности 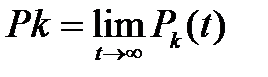 существуют и удовлетворяют уравнениям:
существуют и удовлетворяют уравнениям:
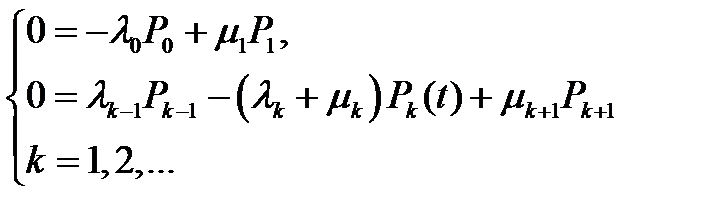
Для решения этой системы введем новые неизвестные
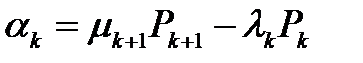 .
.
Тогда наша система будет иметь вид 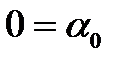 ,
, 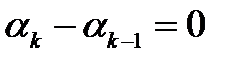 , то есть
, то есть 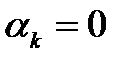 для всех k. Отсюда
для всех k. Отсюда
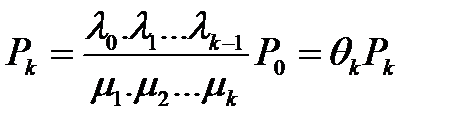 .
.
Так как сумма  , то
, то
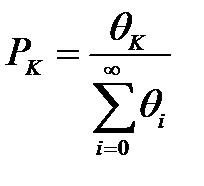 , (3.111)
, (3.111)
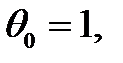
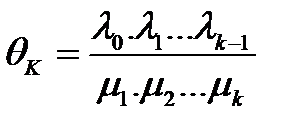
(разумеется, этот вывод справедлив и для конечного числа состояний, нужно присвоить 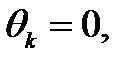 при
при 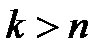 )
)
Теперь для процесса рождения и смерти найдем в явном виде все те характеристики надежности, которые были найдены выше для общего случая.
В моделях теории надежности состояние процесса рождения и смерти Н(t) = k — это, как правило, число неисправных элементов в системе. Тогда из условия монотонности следует [ 23] , что множества 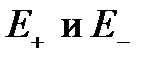 должны быть связаны, то есть:
должны быть связаны, то есть:
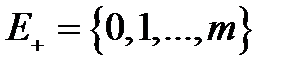 ,
,
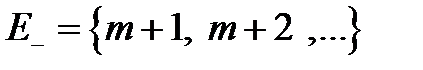
Удобно ввести величины:
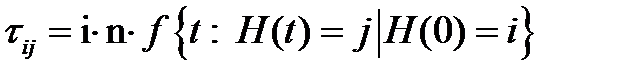
- время достижения состояния j из состояния i . Пусть 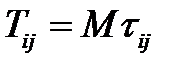 . Заметим, что при переходе из множества
. Заметим, что при переходе из множества 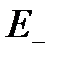 в
в 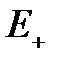 , система всегда попадаем в состояние
, система всегда попадаем в состояние 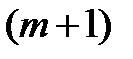 , а
, а
переходя из 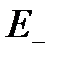 в
в 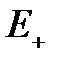 , всегда попадает в состояние m . Поэтому (как и выше, пусть
, всегда попадает в состояние m . Поэтому (как и выше, пусть 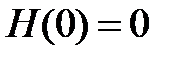 )
)
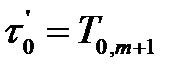 ,
, 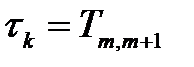
Кроме того, из теории стационарных потоков следует, что
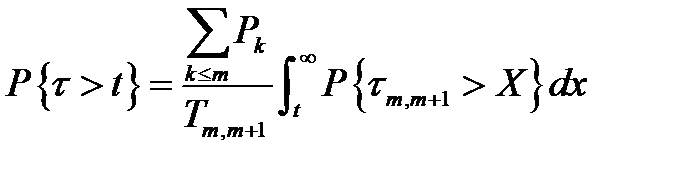 , (3.112)
, (3.112)
(это равенство получается из связи функций Пальма и распределения интервала между соседними точками потока).
Итак, все приводится к нахождению распределения величины 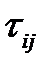 . Так как в моделях теории надежности почти всегда число состояний конечно, то будем считать, что наш процесс рождения и смерти имеет конечное число состояний 0,1,2,..., n (В противном случае распределения
. Так как в моделях теории надежности почти всегда число состояний конечно, то будем считать, что наш процесс рождения и смерти имеет конечное число состояний 0,1,2,..., n (В противном случае распределения 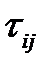 при i > j эффективно не вычисляются).
при i > j эффективно не вычисляются).
Найдем сначала распределение 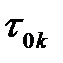 . Пусть
. Пусть 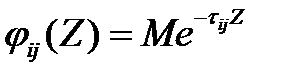 . По формуле (3.95) функции
. По формуле (3.95) функции  удовлетворяют системе
удовлетворяют системе
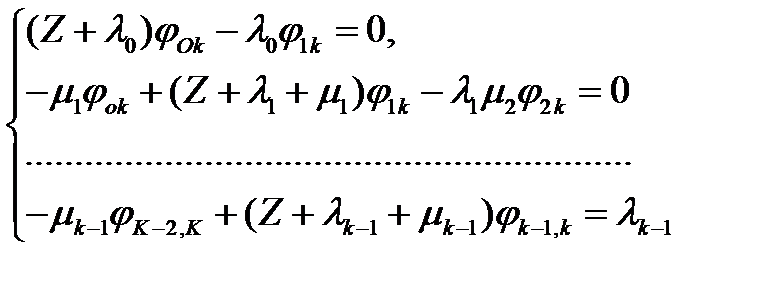
Обозначим определитель этой системы 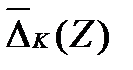 во правилу Крамара, получим:
во правилу Крамара, получим:
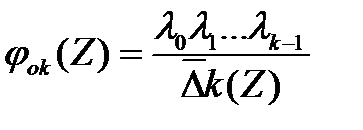 .
.
Раскладывая определитель 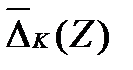 по элементам последнего столбца, можно получить для этих определителей реккурентное уравнение
по элементам последнего столбца, можно получить для этих определителей реккурентное уравнение
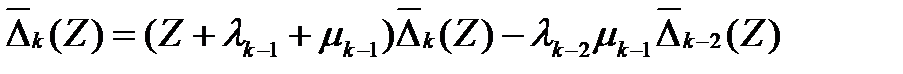 .
.
Введем нормированные определители
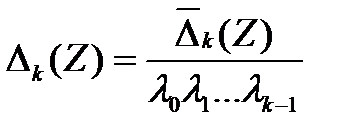 .
.
Для них справедливо уравнение
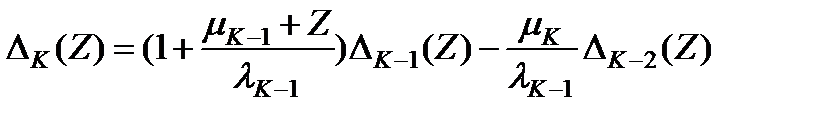 (3.113)
(3.113)
Начальные условия
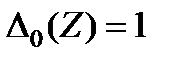 ,
, 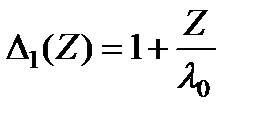
Тогда:
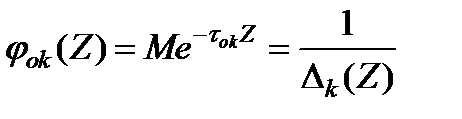 (3.114)
(3.114)
Многочлены 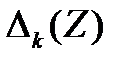 удовлетворяют следующим свойствам:
удовлетворяют следующим свойствам:
1) 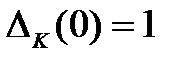
2) все корни 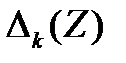 различны и отрицательны;
различны и отрицательны;
3) корни соседних многочленов чередуются, то есть между любыми двумя корнями 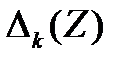 лежит один корень
лежит один корень 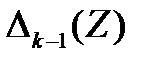
4) модуль максимального по величине корня не превосходит
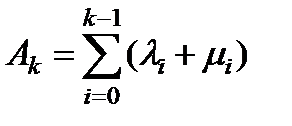 .
.
Эти свойства дают удобный алгоритм для вычисления корней.
Для нахождения распределений 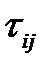 заметим, что при i < j
заметим, что при i < j
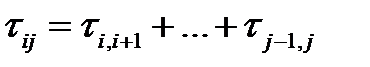 , (3.115)
, (3.115)
где в силу марковости процесса слагаемые независимы. В частности,
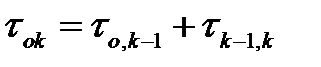
откуда 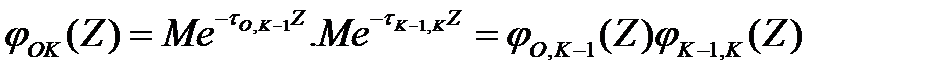
то есть:
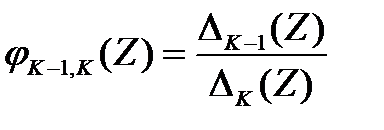 , (3.116)
, (3.116)
а из (3.115) следует, что при i < j
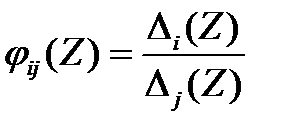 (3.117)
(3.117)
Для того, чтобы быстро найти распре деления 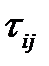 при i > j рассмотрим ''перевернутый ' ' процесс
при i > j рассмотрим ''перевернутый ' ' процесс
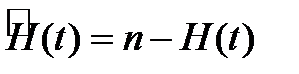 ,
,
его состояниями тоже будут 0,1,2,..., n . Очевидно, что 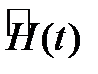 будет процессом рождения и смерти, причем
будет процессом рождения и смерти, причем
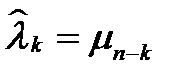 ,
, 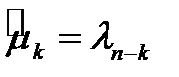
и при 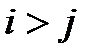
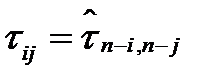
Заменяя в (3.113) 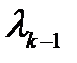 на
на 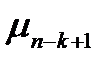 и
и 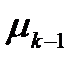 на
на 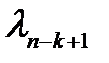 , получим реккурентное уравнение для
, получим реккурентное уравнение для 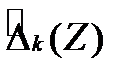
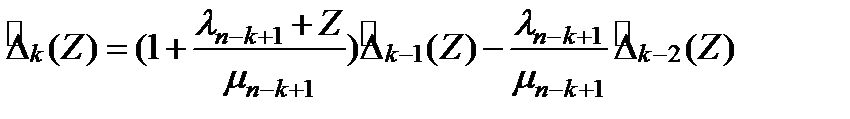 ,
,
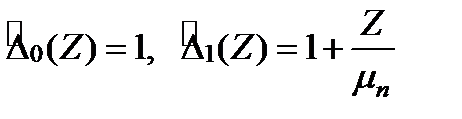 (3.118)
(3.118)
Решая это уравнение, мы находим 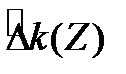 и тогда при
и тогда при 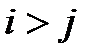
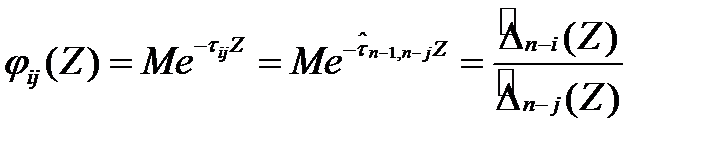 (3.119)
(3.119)
Можно найти выражения для распределений основных характеристик надежности
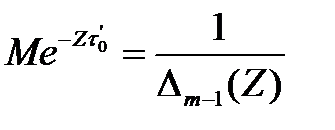 ; (3.120)
; (3.120)
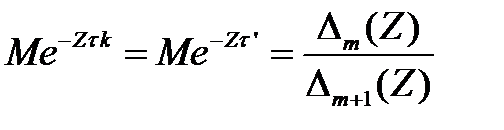 ;
; 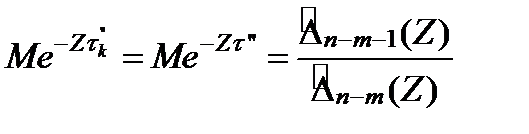 (3.121)
(3.121)
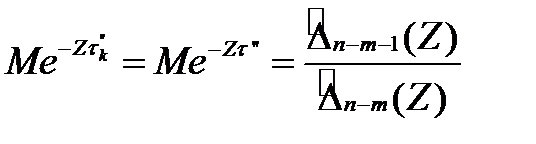 . (3.122)
. (3.122)
Кроме того, из (3.112) и свойств преобразования Лапласа находим:
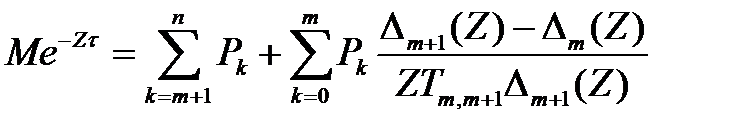 . (3.123)
. (3.123)
В заключение найдем средние значения этих величин.
Коэффициент готовности:
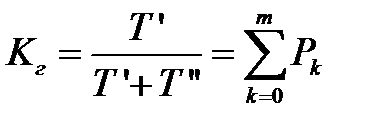 . (3.124)
. (3.124)
Интенсивность потока отказов сиcтемы 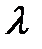 :
:
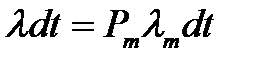 ,
,
для того, чтобы система отказла на [ t , t + dt ] нужно, чтобы в момент t она находилась в состоянии m , вероятность этого 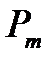 , и на [ t , t + dt ] произошел переход из состояния m в состояние (m+1), вероятность этого
, и на [ t , t + dt ] произошел переход из состояния m в состояние (m+1), вероятность этого 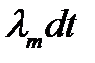 . Итак,
. Итак,
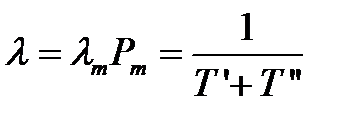 . (3.125)
. (3.125)
Отсюда:
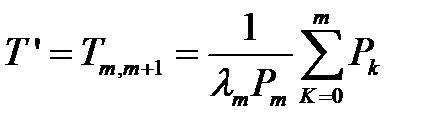 ; (3.126)
; (3.126)
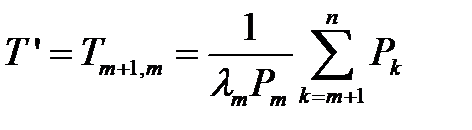 ; (3.127)
; (3.127)
Кроме того, поскольку за m можно взять любое число, то:
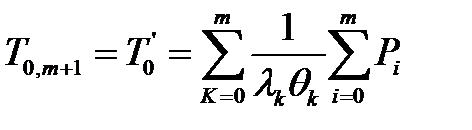 . (3.128)
. (3.128)
И, наконец, из того, что
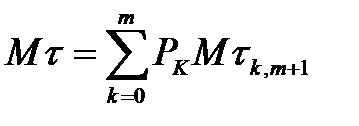
следует:
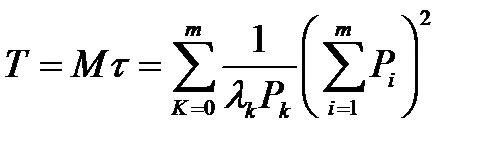 . (3.129)
. (3.129)
Рассмотрим общую модель теории надежности, которая описывается процессом рождения и смерти (см. рис.3.12).
| n-m |
| m |
| λ |
| λ' |
| µ |
Рис.3.12. Модель резервированной системы с восстановлением
Это модель теплого резервирования с восстановлением. Предположим, что имеется ( n- m ) рабочих элементов с интенсивностью отказа 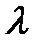 и m резервных элементов с интенсивностью отказа
и m резервных элементов с интенсивностью отказа 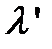 (теплый или скользящий резерв). Каждый отказавший элемент поступает в ремонтное устройство, состоящее из r ремонтных единиц. Каждая единица может одновременно восстанавливать один элемент. Время восстановления имеет показательное распределение с параметром
(теплый или скользящий резерв). Каждый отказавший элемент поступает в ремонтное устройство, состоящее из r ремонтных единиц. Каждая единица может одновременно восстанавливать один элемент. Время восстановления имеет показательное распределение с параметром 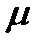 . Если все ремонты единицы заняты восстановлением, то поступающие элементы становятся в очередь. При отказе рабочего элемента на его место мгновенно становится резервный элемент и его интенсивность отказа меняется с
. Если все ремонты единицы заняты восстановлением, то поступающие элементы становятся в очередь. При отказе рабочего элемента на его место мгновенно становится резервный элемент и его интенсивность отказа меняется с 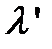 на
на 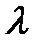 . Восстановившиеся элементы становятся в резерв, а, если все резервные и хотя бы один рабочий элемент отказали, то восстановившийся элемент становится на рабочее место. Этот процесс будет процессом рождения и смерти. В моделях теории надежности состояние процесса рождения и смерти H (t)= k - это, как правило, число неисправвных элементов в системе. Система неисправна, если число неисправных элементов больше m , то есть отказали все резервные элементы и хотя бы один рабочий.
. Восстановившиеся элементы становятся в резерв, а, если все резервные и хотя бы один рабочий элемент отказали, то восстановившийся элемент становится на рабочее место. Этот процесс будет процессом рождения и смерти. В моделях теории надежности состояние процесса рождения и смерти H (t)= k - это, как правило, число неисправвных элементов в системе. Система неисправна, если число неисправных элементов больше m , то есть отказали все резервные элементы и хотя бы один рабочий.
Пусть H (t) - число неисправных элементов в момент t . Интенсивности 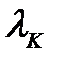 и
и 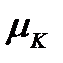 будут иметь следующий вид:
будут иметь следующий вид:
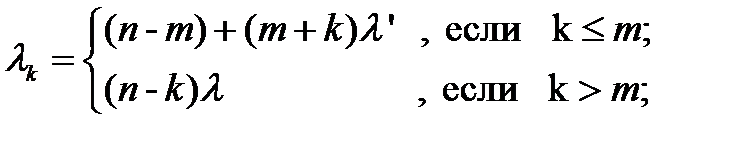
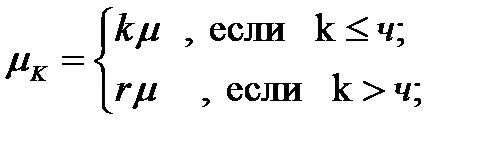
Здесь: 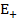 = { 0, 1, 2, ... m }
= { 0, 1, 2, ... m }
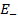 = {m+1, ..., n}
= {m+1, ..., n}
Используя все выведенные выше формулы, можно вычислить характеристики надежности системы.
Поскольку процесс рождения и смерти довольно часто встречается в практике надежности, было бы полезно составить стандартную программу для вычисления характеристик надежности. Входом здесь будут числа 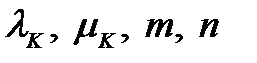 . Программа должна:
. Программа должна:
а) вычислить 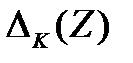 и
и 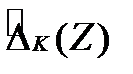 ;
;
б) найти их корни;
в) найти стационарные вероятности;
г) найти распределения величин 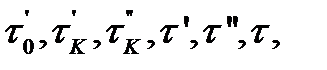 их средние и коэффициент готовности.
их средние и коэффициент готовности.
Дата: 2018-12-21, просмотров: 386.