Допустим, что элементы в системе соединены последовательно, если отказ любого элемента вызывает отказ системы. Подчеркнем, что это - последовательное соединение в смысле надежности оно не означает (для трубопроводной сети), что реальное соединение этих элементов в схеме будет последовательным. Например, элементы в схеме могут быть соединены параллельно, но, если отказ этих элементов есть прекращение подачи воды, то в смысле надежности они будут соединены последовательно. Это важное замечание относится и ко всем дальнейшим пунктам.
Определим для последовательного соединения основные характеристики надежности системы. Система работоспособна в момент t только тогда, когда работоспособны все элементы, то есть:
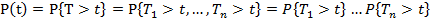 =
=
=Р1 ( t ) P 2 ( t ) .... Pn ( t ) (3.33)
Вероятность отказа системы
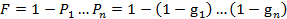
 (3.34)
(3.34)
(ради краткости не будем писать аргумент t).
Если 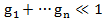 , то можно пользоваться приближенной формулой
, то можно пользоваться приближенной формулой
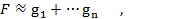 (3.35)
(3.35)
в которой, абсолютная ошибка 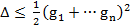
Интенсивность отказа системы в этом случае будет равна:
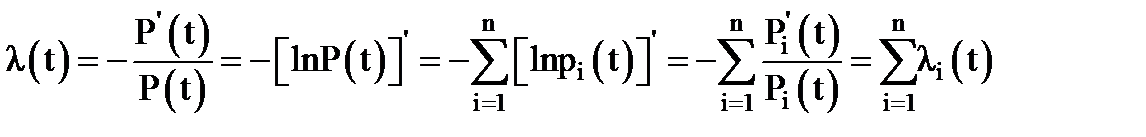
 (3.36)
(3.36)
то есть интенсивность отказа системы равна сумме интенсивностей отказа элементов
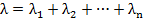
 (3.37)
(3.37)
Отсюда следует, что, если время жизни каждого элемента - экспоненциальное, то и время жизни системы распределено по показательному закону.
Обозначим:
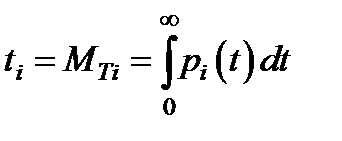 - среднее время жизни i-го элемента;
- среднее время жизни i-го элемента;
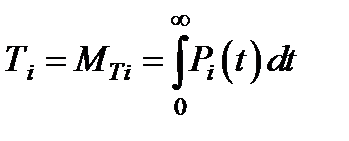 - среднее время жизни системы.
- среднее время жизни системы.
В общем случае время Т не выражается явно как сокупность ti , однако в случае, когда все времена жизни - экспоненциальные, из (3.37) следует:
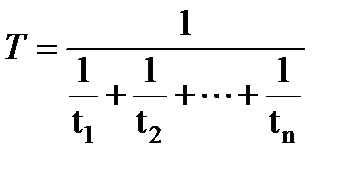
 (3.38)
(3.38)
Из равенства (3.36) видно также, что, если все элементы стареющие, то есть 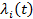 - монотонно возрастает, то и сама система является стареющей, так как
- монотонно возрастает, то и сама система является стареющей, так как 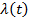 тоже будет монотонно возрастать.
тоже будет монотонно возрастать.
Можно показать, что в этом случае среднее время жизни системы [10,23]:
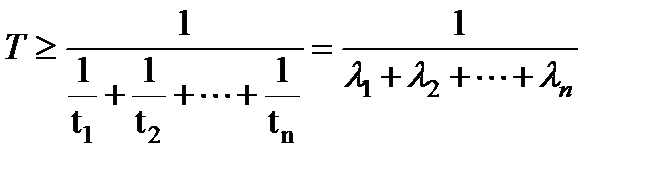 (3.39)
(3.39)
Таким образом, если для стареющих элементов рассчитывается среднее время жизни по формуле (3.38), то при этом занижается истинное среднее время 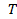 . При большом n это занижение может быть значительным.
. При большом n это занижение может быть значительным.
Если элементы стареют не очень интенсивно, то величина 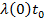 будет лишь немного меньше единицы и в этом случае оценка (3.39) будет достаточно точной.
будет лишь немного меньше единицы и в этом случае оценка (3.39) будет достаточно точной.
Параллельное соединение
Элементы в системе соединены параллельно в смысле надежности, если отказ системы наступает тогда и только тогда, когда отказывают все элементы. Отсюда сразу получаем:
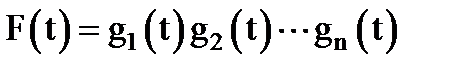 ,
,
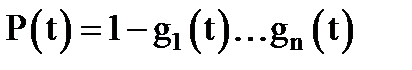
 (3.40)
(3.40)
Параллельное соединение элементов назначается обычно в тех случаях, когда несколько элементов выполняют одну и ту же функцию. Для ее выполнения достаточно одного элемента, поэтому остальные элементы играют роль резервных, а само параллельное соединение часто называют горячим резервом. Понятно, что в такой ситуации элементы чаще всего бывают одинаковыми, то есть:
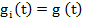 и
и
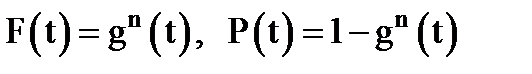
 (3.41)
(3.41)
Если 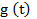 - стареющее распределение, то и F (t) - стареющее распределение [10 ] .
- стареющее распределение, то и F (t) - стареющее распределение [10 ] .
Среднее время жизни системы
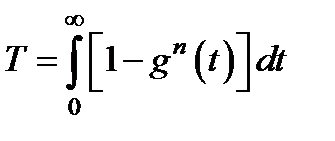
 (3.42 )
(3.42 )
вычисляется в явном виде очень редко. Например, для случая g(t)= 1- 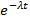
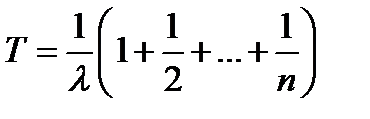 (3.43 )
(3.43 )
C другой стороны, при большом n , как видно из (3.42 ), среднее время в основном зависит от поведения функции распределения при больших t . Но поведение “хвостов” распределений мы обычно знаем очень плохо. В этих условиях желательно иметь для среднего Т пусть очень грубую, но простую оценку. Такую оценку можно получить.
Пусть распределение g(t) - стареющее, тогда справедливо неравенство
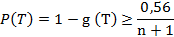
Теперь предположим, что функция надежности элемента р(t) обладает следующим свойством - касательная к графику p(t), проведенная в точке t = Т, лежит ниже этого графика. Тогда справедливо неравенство:
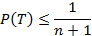
Если распределение p ( t )- стареющее, то тогда [10, 23]
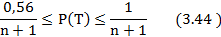
Неравенство 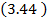 очень удобно. Если дан график р(t) то мы берем на оси ординат две (а и b) точки (см. рис. 3.3 ):
очень удобно. Если дан график р(t) то мы берем на оси ординат две (а и b) точки (см. рис. 3.3 ):
| P(t) |
| 1 a b |
| n=3 |
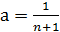 и и 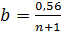 , ,
|
0 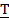 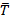
|
| t |
Рис. 3.3. Интерпретация интервала оценки среднего времени Т стареющего элемента
проводим через них горизонтальные прямые до пересечения с графиком р(t) , получаем две точки на оси абсцисс 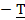
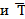 . Если мы уверены , что элемент стареющий, и, если проверили, что касательные к графику р(t) на
. Если мы уверены , что элемент стареющий, и, если проверили, что касательные к графику р(t) на  участке
участке 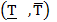 лежат ниже графика, то справедливо неравенство
лежат ниже графика, то справедливо неравенство 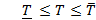 .
.
Отметим ещё, что на практике часто встречается такое соединение элементов - система из n одинаковых элементов исправна тогда и только тогда, когда исправно не менее m элементов. Для этого сличая
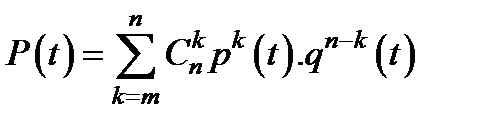 ,
, 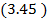
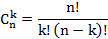
При m = n получается последовательное соединение, а при m = 1 - параллельное. Для этого случая также можно получить оценку типа 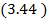 .
.
Дата: 2018-12-21, просмотров: 386.