В системах водоснабжения не всегда применяется параллельная работа элементов с нагруженным резервом. Чаще для обеспечения надежности системы  используется схема с резервированием ее элементов ненагруженным резервом. При такой схеме используется работа основных  элементов системы,  а другая часть (резервных) элементов  вступает  в работу только при отказе одного или нескольких основных элементов. 

        Работа элементов в системе с ненагруженным  резервом  обычно требует контрольных при­боров, с помощью которых обнаруживаются  отказы элементов, и   устройства переключений, которые позволяют включать резервные элементы в работу. Предположим, что при­бор, обнаруживающий отказ, и переключатель имеют 100%-ную надежность и что работающие и резервные элементы имеют одинаковую интенсивность отказов  l.

Можно рассматривать группу основных и  резервных элементов как еди­ную систему (например, противопожарная насосная станция) , в которой допускается несколько отка­зов до того, как система окончательно прекратит выполнение своих функций. Если для резервирования одного основного эле­мента (насосного агрегата) включаются п резервных  элементов (насосных агрегатов) , мы имеем в системе п +1 эле­ментов, и в ней может произойти п отказов, не вызывая отказа системы. Только отказы (п +1) элементов вызовут отказ всей системы. Используя теорему полной вероятности можно записать:

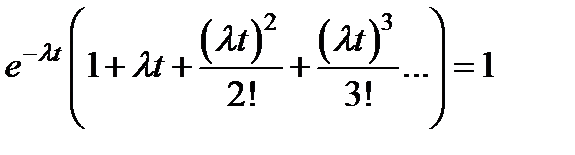          (3.29)

          В этом выражении величина ( 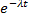× 1) представляет собой вероят­ность того, что не произойдет ни одного отказа, величина (  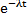×lt ) дает вероятность того, что произойдет один отказ,  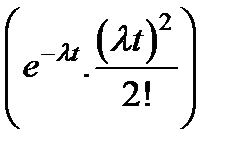     вероятность того, что произойдут два отказа, и т.д. Следовательно, вероятность того, что произойдет один отказ или не произойдет ни одного отказа, равна 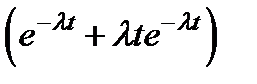, вероятность того, что произойдет не более двух отказов, равна 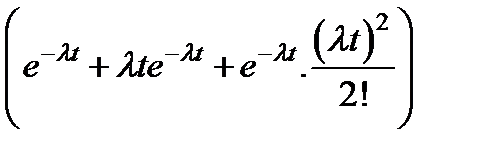и т. д. Эти вероятности представляют собой надежность много­кратно резервированных систем, состоящих из одинаковых элементов, т. е. из элементов, имеющих одинаковую интенсив­ность отказов.

       Если обозначить через Р_нн и F_нн соответственно надежность и ненадежность всей системы с ненагруженным резервом, то, поскольку Р_нн +F_нн = 1, можно написать:

.

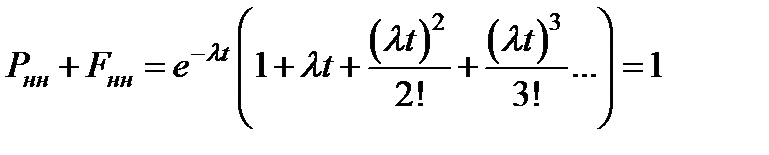
       Если допускается один отказ, то

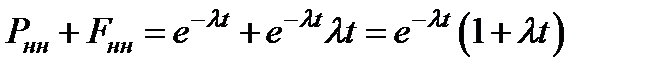                         (3.30)

       Формула (3.30) представляет собой надежность системы при ненагруженном резерве, состоящей из одного работающего и одного резервного элемента с интенсивностью отказов l.

       Поскольку в системах водоснабжения подобные методы резервирования элементов применяются сравнительно редко, ограничимся приведенной выше информацией. 

 3.4. Надежность невосстанавливаемой системы с независимыми элементами

       Системы водоснабжения, как правило,  восстанавливаются. Однако условия восстановления различны: в одних системах элементы восстанавливаются непрерывно (насосные агрегаты на насосных станциях жилищно-коммунального водоснабжения), в других системах (трубы в системах подачи и распределения воды)  элементы восстанавливаются  после отказа либо износа. В этой связи, если исключить периоды приработки и износа, то подобные системы на интервале времени "нормального периода жизни" можно рассматривать как невосстанавливаемые. А потому, эти модели заслуживают внимания со стороны любого специалиста в области водоснабжения. 

        Предположим, что система состоит из n элементов. Вре­мя жизни   i -го элемента есть случайная величина 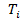 с функцией распределения      

,

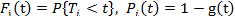       где 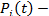вероятность безотказной работы i -го элемента до момен­та t.

       Элемен­ты не восстанавливаются и все время Т_i- независимы.

       Состояние i -го элемента в момент t, будем задавать функцией X i( t ):

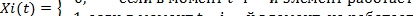
       Тогда состояние всех элементов задается двоичным вектором

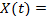 [x₁(t), x₂(t), x₃(t), ××× , x_n(t)]

       Допустим, что система может находиться тоже только в двух состояниях - исправном или неисправном, соответственно:

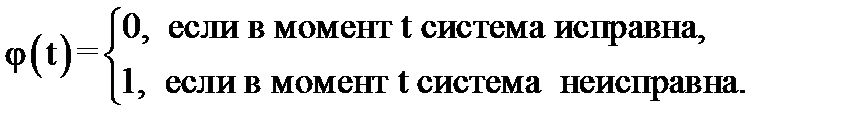
        При этом, состояние элементов в каждый момент времени однозначно определяет состояние системы, то есть:

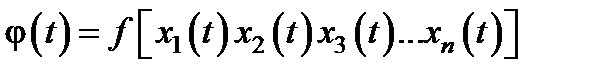
       В теории надежности логическая функция  f  удовлетворя­ет одному важному условию. Для того, чтобы его сформулировать, введем на множестве двоичных векторов упорядоченность - скажем, что

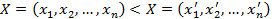если для всех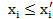

       Тогда условие на функцию f записывается так:

если X < 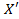, то f (X) < f ( 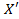,)                       (3.31)

       Смысл этого ограничения очень прост - дополнительные отказы . элементов не могут перевести систему из неисправного состоя­ния в исправное.

       Множество 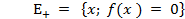- это множе­ство исправных состояний системы, а множество - это множество неисправных состояний

система.

       Пусть T- время жизни системы, 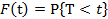       - вероятность отказа системы до момен­та t, 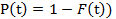- вероятность безотказной работы си­стемы до момента t.

       В принципе можно  написать выражение для функции надежности системы:

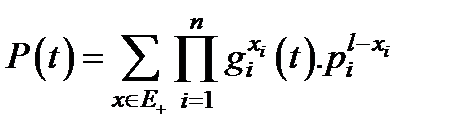 (3.32)

произведение, стоящее под знаком сумма, есть вероятность того, что элементы находятся в состоянии X). На самом деле фор­мула (3.32) позволяет рассчитать надежность системы только для нескольких простых случаев. Дело в том, что число элементов  n - велико, а число состояний элементов, равное 2 ⁿ  , бу­дет астрономически велико, и  никакая машина не в состоянии сосчитать сумму (3.32).

       Соловьев А.Д. [ 23] предложил  несколько мето­дов, позволяющих рассчитывать надежность подобных   си­стем.    При  описании  этих систем, предлагается  говорить о способах соединения элементов в системе так, как будто это трубопроводная сеть. Такой язык удобен, но следует понимать, что он ус­ловен и, говоря о соединении элементов в системе, мы лишь опи­сываем на этом языке логическую функцию f (x).