При проектировании системы водоснабжения, недостаточно,  просто выбрать число ее элементов по заданным характеристикам.   Необходимо убедиться, что требуемая величина надеж­ности  системы при этом обеспечивается. Если уровень надежности системы  не достаточен, то применяется  резервирвирование  ее элементов. Виды резервирования разнообразны [ 2 ,3, 6, 7, 10, 23 ]: нагруженный резерв, ненагруженный резерв, облегченный резерв, восстанавливаемый резерв, невосстанавливаемый резерв, постоянное резервирование, скользящее резервирование, резервирование замещением и т.д.

Расчет надежности системы (например, двух водоводов) при постоянном резервирова­нии  ее элементов, соединенных параллельно, можно выполнить по формулам  (3.7) и (3.8).

Однако часто параллельно работают больше чем два эле­мента (водовода). Возможна параллельная работа трех, четырех … и n элементов. Тогда необходимо оценивать вероятности появления не двух, а n  событий. Например, если в системе параллельно работают 3 элемента: А, В, С, с параметрами надежности Р(А), Р(В) и Р(С), то     вероятность того, что   система будет безотказно функционировать рассчитывается по формуле

Р(А Ú В Ú С) = Р(А) + Р(В) + Р(С) — P(A)P(B)-P(A)P(C)-P(B)P(C) + P(A)P(B)P(С)

Если все три элемента равнонадежны, т. е.

                       Р(А) = Р(В) = Р(С) = Р,

       то

Р(А Ú В Ú С) = 3Р — 3Р² + Р³             (3.17)

Аналогично можно рассчитать надежность системы  состоящей из четырех параллельно работающих элементов. Подобные расчеты утомительны.   Существует более простой способ расчета надежности параллельно работающих элемен­тов. Используя формулу Р + F= 1, вычисляем вначале ненадеж­ность F, а затем, вычитая ее из 1, получаем величину надеж­ности. Например,  вероятность отказа двух элементов F = F ₁ F₂. Вероятность отказа трех па­раллельно работающих элементов F = F ₁ F ₂ F₃ , а ненадеж­ность  п  параллельных элементов

F ( t )_н= F ₁ ( t ) F ₂ ( t ) F ₃( t ) и ××× F _n( t ) = 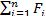( t )      (3.18)

Тогда надежность n работающих параллельно элементов выра­жается в виде 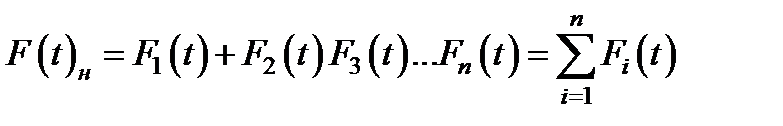                    (3.19).

       Метод предварительного вычисления ненадежности F ( t )_н как про­изведения ненадежностей элементов чрезвычайно облегчает рас­четы надежности параллельного соединения.

       На практике для быстрой оценки величины ненадежности элементов часто используется довольно простой способ апроксимации. Если допускать, что вероятность безотказной работы каждого элемента имеет экспоненциальное распределение, то

,

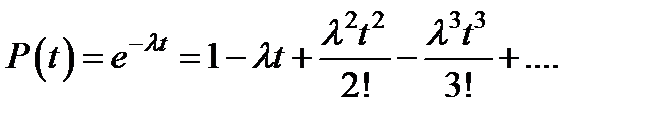       получаем

.

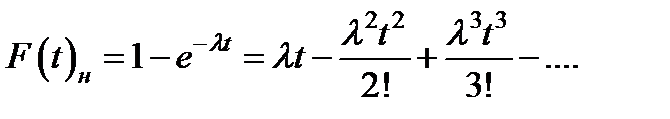       Когда  l t  существенно  меньше единицы, l t < 0,1, можно с незначительной по­грешностью пренебречь членом  и последующими слагае­мыми, в результате чего получаем

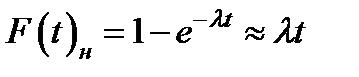              (3.20)

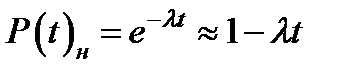               (3.21)

      Мгно­венная интенсивность отказов систем параллельно соединенных элементов является функцией времени работы t, тем не менее среднюю наработку на отказ системы можно рассматривать как стационарную величину. Например, для системы из двух параллельных элементов (см. рис. 3.2. "а")

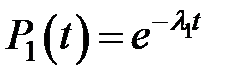
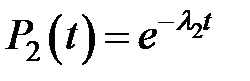
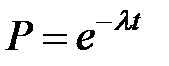
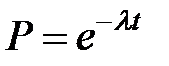
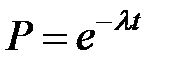
          а )                                                          б)

Рис. 3.2. Системы с параллельновключенными элементами: а) -  с двумя параллельно включенными элементами ;     б) - с тремя параллельно включенными элементами

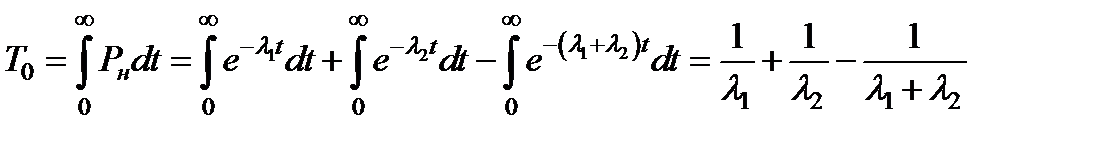
(3.22)

       Если надежности элементов системы одинаковы, то средняя наработка на отказ будет равна

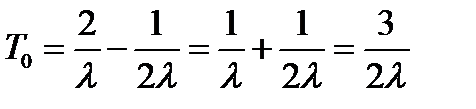
                                         (3.23)

Аналогично, для трех одинаковых элементов, работающих параллельно (см. рис. 3.2 "б")

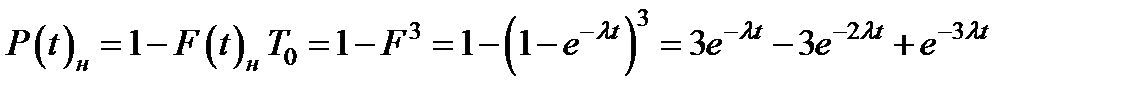  (3.23)

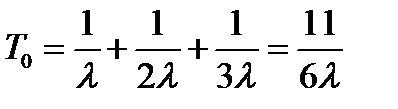
      (3.24)

      Когда три элемента, работающие параллельно, неодинаковы,  

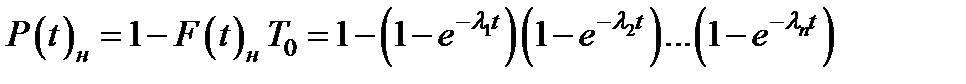                                        (3.25)             

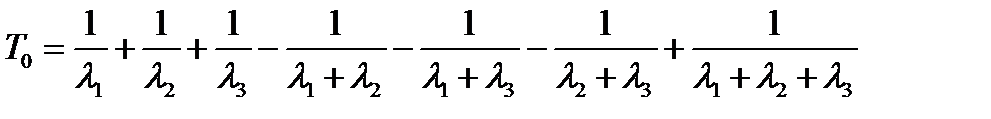
(3.26)

          Наконец, для  п одинаковых элементов, работающих параллельно

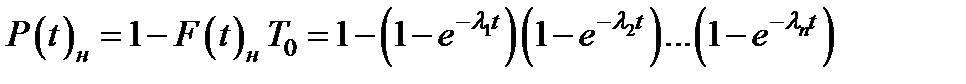    (3.27)

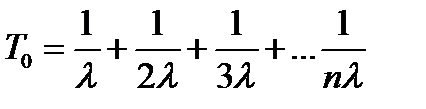                                                 (3.28)