1 . Случай мгновенного восстановления.
Предположим, что элемент, начавший работать в момент t = 0 ,
в некоторый момент tj = t j отказывает. Ранее приводились оценки надежности элемента только до момента tj = t j, будущее нас не интересовало. На практике, если элемент является достаточно сложным или дорогим устройством, его восстанавливают (при условии, что это возможно). Если неисправное изделие ремонтировать не целесообразно, его заменяют на новое. Обычно в теории надежности [2, 3, 23] эти два типа восстановления элементов не различают и называют одним словом - восстановление.
Итак, в момент t1= t 1, начинается восстановление элемента. Предположим , что время восстановления мало по сравнению со временем жизни. Тогда можно им пренебречь и считать, что восстановление - мгновенное. После восстановления элемент начинает работать и через времяt 2 снова отказывает. В момент отказа t2 =t 1 +t 2, происходит второе восстановление и так далее (см. рис. 3.1).
| 0 t1 t2 ……. tn t tn+1 |
| t1 t2 |
| ξt |
Рис. 3.1. Интерпритация процесса жизни и мгновенного восстановления элемента
Обычно вводится допущение, что периоды жизни t 1 , t 2. · · · t n независимы и одинаково распределены, для которых справедливы условие:
Р {t k < t }= F ( t ), M t k = T , D t k = 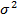 , f ( t )=
, f ( t )= 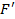 ( t )
( t )
Если восстановление заключается в замене, то это условие выполняется. В случае ремонта это условие справедливо сравнительно редко (например, когда ремонт состоит в том, что устраняются видимые неисправности). Чтобы учесть зависимость t k от предыдущих t 1 или t 2 · · · t n и т.д. , надо знать структуру элемента и надежность его частей, и рассматривать элемент как систему.
2. Процесс восстановления.
Процесс восстановления можно рассматривать как поток случайных точек 0 < t1 < t2 < · · · tn < · · ·. Раздел математики, изучающий этот процесс, называется теорией восстановления. В этой теории изучаются или оцениваются различные характеристики процесса, которые в теории надежности называются характеристиками надежности.
Введем обозначение: F n ( t ) = P {t n < t} , которая определяет рекуррентно,
F n +1 ( t ) = 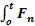 ( t - x ) d F ( t ) , F 1 ( t ) = F ( t ), f n ( t ) = F '( t ).
( t - x ) d F ( t ) , F 1 ( t ) = F ( t ), f n ( t ) = F '( t ).
3. Пуассоновский поток.
Пусть F ( t ) = 1- 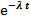 , то есть время жизни элемента имеет показательное распределение. В этом случае процесс восстановления называется пуассоновским потоком.
, то есть время жизни элемента имеет показательное распределение. В этом случае процесс восстановления называется пуассоновским потоком.
В этом случае f ( t ) = l 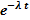 .
.
Так как f n +1 ( t ) = 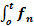 ( t - ) f ( x ) d x , то интегрируя последовательно, находим
( t - ) f ( x ) d x , то интегрируя последовательно, находим
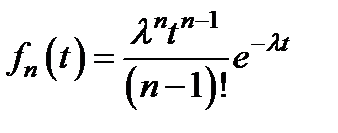
т.е. момент tn имеет гамма-распределение с параметром n .
Интегрируя f n ( t ), получим :
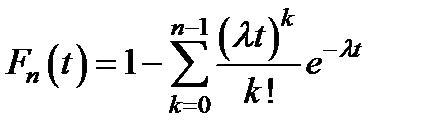
откуда
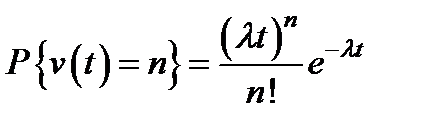 . (3.17)
. (3.17)
Это основная формула в теории пуассоновского потока.
Плотность восстановления
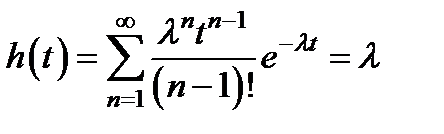 .
.
Следовательно, для пуассоновского потока плотность восстановления совпадает с интенсивностью отказа. Далее:
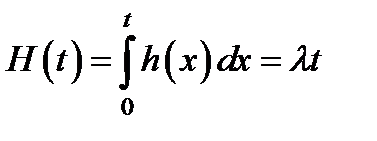
Найдем распределение остаточного времени жизни
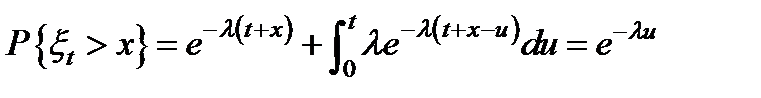 ,
,
т.е. остаточное время жизни элемента имеет такое распределение, как и полное время жизни.
Дата: 2018-12-21, просмотров: 392.