Выше отмечалось, что деление объекта на элементы системы весьма условно.  Элемент - это такой объект, надежность которого изучается сама по себе, независимо от его структуры и надежности составляющих его частей. Наоборот, система - это объект, надежность которого оценивается по его структуре и надежности его элементов. Таким образом, один и тот же объект мы можем рассматривать и как элемент, и как систему.

Если надежность объекта можно оценить при "испытании", то он рассматривается как одно целое. В противном случае объект рассматривается как система, которая состоит из отдельных элементов с заданной (или полученной в ходе "испытания") надежностью. Сочетание элементов формирует простую или сложную систему, с точки зрения методов ее расчета надежности.   Существует точная математическая связь между надежностью системы и надежностью ее элементов.

 Уровень надежности элемента определяется из испытаний, которые дают информацию об интенсивности отказов.    Чем прочнее элемент, тем меньшей интенсив­ностью отказов он будет обладать.   Действительная ин­тенсивность отказов, определяющая вероятность безотказной работы, зависит от случайных факторов, действующих в про­цессе производства, и от случайных изменений условий эксплуа­тации элемента.  Она зависит от соотношения между прочностью, закладываемой в элемент (оборудование, сооружение)  при проектировании, и многообразия условий функционирования.              

       Расчеты надежности систем основаны на двух важных операциях: 1) на оценке  с максимально возможной точностью надежности элементов, используемых в дан­ных условиях работы системы; 2) на расчетах надежности раз­личных комбинаций этих элементов.

 Моделью надежности системы из последовательных элементов называют систему, в которой отказ любого элемента приводит к ее отказу.

Ранее отмечалось, что длительные испытания  (большой объем статистических данных) дают более точную  ин­формации о действительной надежности элемента. Расчет на­дежности системы проводится тогда при помощи нескольких сравнительно простых и точных теорем теории вероятностей.    После того как по­лучены правильные количественные характеристики надежности элемента в системе или хотя бы хорошие оценки этих харак­теристик, можно точно рассчитать надежность всей системы, даже когда система представляет собой наиболее сложную мыс­лимую комбинацию элементов. Степень точности   резуль­татов расчета  не зависит от аппарата теории вероятностей, так как ве­роятностные соотношения сами по себе совершенно точны; достоверность расчетов зависит в основном от точности данных о надежности отдель­ных элементов.

В расчетах надежности системы используются следующие основные правила теории вероятностей:

1) Если А и В — два независимых события, вероятности ко­торых Р(А) и Р(В), то вероятность того, что имеют место оба события, равна произведению

Р(АВ) = Р(А) · Р(В).                     (3.1)

2) Если достаточно, чтобы из двух совместимых событий произошло хотя бы одно — А или В — или оба вместе, то

Р (А Ú  В) = Р (А)+Р(В) — Р(А) · Р(В).          (3.2)

3) Если события несовместимы, т. е. когда происходит одно, другое событие не может произойти, формула (3.2) упрощается:

            Р(А Ú  В) = Р(А) + Р(В).                                 (3.3)

4) Если два события не только несовместимы, но и противо­положны, т. е. когда не происходит  А, происходит В ( 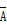), и на­оборот, из (3.3) получаем

                                P(A) + P(B) = 1.                          (3.4)

Случаи 1 и 2 — противоположные события, т. е.  Р_посл +F_посл = l, поскольку противоположное событие для безотказ­ной работы двух элементов осуществляется тремя путями: или отказывает один элемент, или другой, или оба вместе. Следо­вательно, величины Р_посл и F_посл можно соответственно на­звать надежностью и ненадежностью последовательного соеди­нения элементов, или последовательной системы. Это означает, что отказ любого элемента приводит к отказу системы.

Случаи 3 и 4 — также противоположные события, т. е. Р_пар +F_пар = l, так как противоположное событие для двух отказавших элементов есть событие, когда один или об эле­мента работают безотказно. Р_пар и F_пар  называются соответ­ственно надежностью и ненадежностью параллельного соединения элементов, или системы с нагруженным резервом. Это означает, что если отказал один элемент, то существует другой элемент, который выполняет требуемую функцию, и, следовательно, такая параллельная система из двух элементов не от­казывает, если отказал один элемент. Очевидно, что если имеется более двух элементов, включенных параллельно, например п элементов, система не откажет до тех пор, пока работает хотя бы один элемент. Следовательно, из п параллельных элементов допускается отказ п - 1 элемента, и это не приводит к отказу системы при условии, что один оставшийся элемент удовлетво­рительно выполняет требуемую функцию.

  При рассмотрении элементов с не экспоненциальным распределением отказов необходимо учитывать, что интен­сивности их отказов не постоянны, а являются функцией нapaботки  Т  этих элементов. Поэтому,   для заданного времени, для которого определяет­ся надежность, необходимо использовать интенсивность отказов элемента, соответствующую его наработке к этому времени.

  В большинстве случаев закономерности отказов элементов в системе удается достаточно точно описать экспоненциальной функцией; это всегда возможно, если момент воз­никновения отказов учитывается  за время  суммарной наработки системы или когда элементы работают только в течение своего периода нормальной эксплуатации (т. е. проводится профилактическая замена). В  случае, когда интенсивность отказов постоянна, с экспоненциальным распределением, формулы (3.1) — (3.2) могут быть представлены в виде:

Р_посл (t)  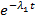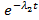= 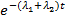· =            (3.5)
              F _пос  (t) = 1- 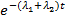                 (3.6)

Р_пар(t)  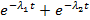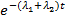=  -            (3.7)
    F _пар  (t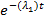) = (1-  ) (1- 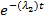 )                (3.8)

Сложные системы обычно состоят из большого числа эле­ментов или блоков, соединенных последовательно, что озна­чает, что система отказывает при отказе любого элемента или блока. В некоторых случаях к заведомо малонадежным элементам системы   для повышения надежности подключаются резерв­ные элементы; иногда к целым группам элементов подклю­чаются такие же или подобные группы, включаемые парал­лельно. Случай двух параллельно работающих водоводов, каждый из которых имеет 50% пропускную способность. Каждый из водоводов имеет только один  ремонтный участок (труб соединенных в трубопровод, который ограничивается переключающими устройствами) - элементов.

Такие параллельные соединения из двух или более эле­ментов или групп элементов можно рассматривать как блоки, соединенные последовательно, т. е. система отказывает, если отказывает такой блок в целом.

Для  п  элементов или блоков, соединенных последовательно, надежность системы выражается формулой

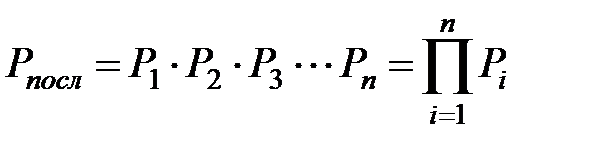                                    (3.9)   

где 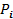 - надежность i-го элемента или блока в последовательном соединении.  

       Формула (3.7) является фундаментальной формулой для расчета на­дежности сложных систем . Эта формула называется законом произведения надежностей.                                                                                                                                                                                                                              

Когда надежность каждого элемента  в системе оценивается по экспонен­циальному закону, то формула (3.7), определяющая надежность системы, упрощается и принимает вид

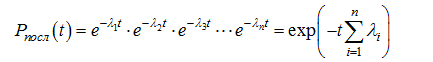(3.10)  

       В качестве простого примера предварительного анализа надежности рассмотрим водовод, состоящий из «последовательно» соединенных ремонтных участков, одинаковой длины каждый,  с экспоненциальным  законом надежности. Ремонтные участки смонтированы: 1-  из стальных труб с защитными покрытиями, 2 - из чугунных с защитными покрытиями, 3- из полимерных труб. Предположим, что ремонтные участки работают равное количество времени с момента монтажа, в равных условиях эксплуатации.

При этих условиях участки имеют следующие интенсивности отказов:

       1 - l₁ = 5,7 ·10^-6 1/час

       2 - l₂ = 4,56 ·10^-6 1/час

       3 - l₃ = 7,6 ·10^-6 1/час.

Сначала складываем все интенсивности отказов

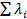        = 5,7 + 4,56+7,6) 10^-6 = 17,86· 10^-6 1/час

Эта сумма представляет собой интенсивность отказов всего водовода. Оценим надежность системы для заданного времени t=8760 часов (время работы от ревизии до ревизии)

Р_посл ( t ) = 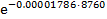= =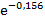0.9

Следовательно, от этой системы можно ожидать с вероятностью

Р_посл (8760 )=0,9 , что система водоводов имеет среднюю наработку на отказ 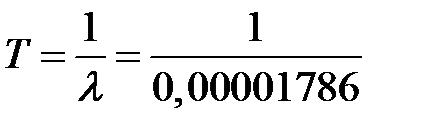 = 55 991 часов = 6,39 лет.

  Конечно, каждый вправе сомневаться в том, насколько точны вероятностные расчеты. Могут ли они дать ответы, достаточно близкие к истинным?  Если число испытаний мало, оценка может существенно отличаться от истинной вероятности; она может быть завышенной или заниженной, но может быть и близкой к истинной вероятности. Оценками, полученными по результатам небольшого числа испытаний, нужно пользоваться осторожно. Количество «испытаний», из которых получена оценка вероятности, является мерой достоверности полученной оценки. Не в меньшей мере на точность оценки влияет и соблюдение единиц измерения исследуемых величин. Так надежность задвижек, обратных и предохранительных клапанов, которые работают совместно с трубопроводами, насосами в системе, часто выражают количеством циклов при переключениях. Время работы трубопровода непрерывная величина, а цикл задвижки - периодическая. Складывать эти величины, как это часто делается инженерами, - недопустимо. Необ­ходимо переводить значение интенсивности отказов за рабочий цикл в единицы интенсивности отказов за время работы системы. Только после этого для численных расчетов можно использо­вать формулу (3.8). Число циклов   можно связать с наработкой, измеряемой  в часах, особенно в тех случаях, где существует некоторая регулярность рабочих циклов. Переход от циклов к часам может быть очень полезен при сложных вероятностных расчетах. Такой переход приводит надежность  элемента к общему параметру и значительно упрощает математические выкладки. 

 Перевод в интенсивность отказов за время t работы бывает необходим также для элементов со случайными промежутками занятости в течение общего периода работы си­стемы (например, насос на насосной станции, запорная арматура), хотя интенсивность их отказов тоже выражается числом отказов за время t .

Время t в формуле (3.8) —время работы системы. Только в том случае, когда элемент работает в системе непрерывно, время его работы совпадает с временем работы системы. На­пример, если элемент должен работать всего 1/ 1000  вре­мени работы системы t, то интенсивность его отказов в масштабе времени работы си­стемы будет  l'/1000.

В общем виде, когда элемент работает в среднем t₁ час за t  работы системы, интенсивность отказов элемента в мас­штабе времени работы системы выражается формулой

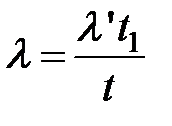                                               (3.11)

Эта приведенная интенсивность отказов элемента может быть использована в (3.8) для элементов со случайными про­межутками занятости. Если t₁ составляет весьма малую часть t, то элемент может оказаться высоконадежным в масштабе вре­мени работы системы, даже если интенсивность его отказов сравнительно высока при непрерывной работе.

Формула (3.9) основана на предположении, что в отклю­ченном или обесточенном состоянии элемент имеет нулевую интенсивность отказов, хотя система в это время работает.

Но это не всегда так. Интенсивность отказов элемента может не быть равной нулю даже в обесточенном или в отключенном со­стоянии. Если l'— интенсивность отказов в рабочем, а l"— в выключенном состоянии и если элемент в течение t час работы t₁  час находится в рабочем состоянии, a t₂=t- t₁ час _- в вы­ключенном, то поведение элемента в системе будет описываться средней интенсивностью отказов, равной

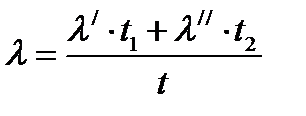                                     (3.12)

Формула (3.10) выражает, следовательно, интенсивность от­казов элемента в масштабе времени работы системы [ 3] .

Если интенсивность отказов элемента выражается в едини­цах рабочих циклов, т. е. значением l_с за один рабочий цикл, и если элемент в среднем совершает   с операций за t час ра­боты системы, элемент в системе будет иметь интенсивность от­казов

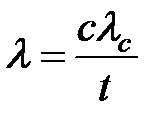                                       (3.13)             

Но если элемент к тому же обладает зависящей от времени ин­тенсивностью отказов l' во включенном состоянии и интенсив­ностью отказов l" в выключенном, интенсивность отказов эле­мента в масштабе времени работы всей системы будет равна

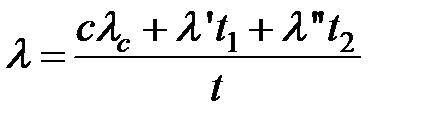                (3.14)

Очевидно, что в этой формуле t₁ + t₂ = t, где t — заданное время работы системы.

Формулу (3.12) можно рассматривать как общую формулу для расчета интенсивностей отказов элементов в масштабе вре­мени работы системы. Для большинства элементов (переключателей, регулирующей арматуры) величиной l" можно пренебречь, за исключением тех случаев, когда воз­действие нагрузок на элемент в работающей системе очень ве­лико, даже если сам элемент выключен (из-за коррозии металла). Интенсивность отказов некоторых устройств, в частности переключающих (запорной арматуры), почти пол­ностью определяется величиной l_с, так что в этих случаях ве­личиной l' также можно пренебречь; для других элементов, в частности для элементов, включаемых на длительное время, определяющей является как раз зависящая от времени интен­сивность отказов l'. Но имеется и категория элементов,   для которых не­обходимо учитывать как l_с, так и l'. Такие элементы обычно являются надолго включаемыми элементами, поскольку  в них возникают процессы износа при включениях и выклю­чениях, а также коррозии.  

 Практически влияние переключения не будет столь значи­тельным, так как сумма зависящих от времени интенсивностей отказов других элементов в системе обычно гораздо больше, чем интенсивность отказов за цикл переключающих устройств, которые совершают один цикл переключений за время выполнения задания.

  Однако если переключающее устройство совер­шает большое число циклов за время выполнения задания или если система содержит много переключающих устройств, чувствительных к  перепадам давлений, вызванным переключениями , то частота включения и отключения этих устройств  за время t  должна учитываться при расчетах надеж­ности системы.

Иногда возникает вопрос, не лучше ли, не экономичнее ли оставлять такие  элементы включенными, даже когда не требует­ся работа системы? Что выгоднее, с точки зрения надежно­сти, — определяется отношением вероятности безотказной ра­боты за t  пребывания во включенном состоянии, когда в этом нет необходимости, к вероятности безотказной работы за цикл одного включения. Таким образом, критерий для выбора режима использования объекта получается в виде отношения ожидаемых чисел отказов для двух случаев

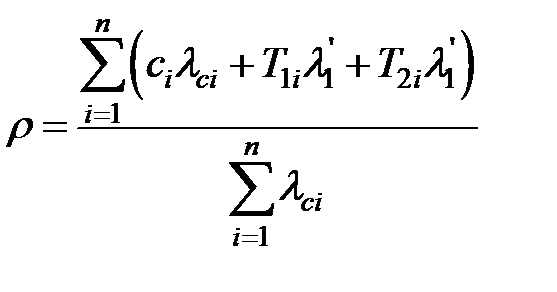                   (3.15)

где T ₁ + T ₂ = T. Если r > 1, более высокая надежность достигает­ся выключением системы на T -часовой промежуток, когда не требуется функционирования системы. Если r <1, более высо­кая надежность достигается, когда систему оставляют вклю­ченной на T -часовой промежуток времени, т. е. вплоть до на­чала выполнения следующего задания. Но, очевидно, что   r  может стать меньше единицы, только если  в формуле (3.15) числитель будет меньше знаменателя. Это может случиться, например, если за промежуток времени  Т , когда система остается вклю­ченной, ни один элемент не переключается, т. е. с = 0. Если за время Т  все элементы системы включены, среднее число отказов  будет 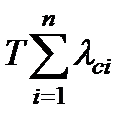 Оно должно быть меньше среднего числа отказов системы за одно включение 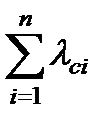. Требование r < 1 выполняется, если длительность промежутка   Т  меньше отношения интенсивности отказов системы за один переключающий цикл или за одно  включение к интенсивности отказов за один час не­прерывной работы:

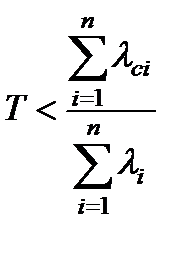                  (3.16)

Очевидно, что величина  Т может быть важна только для си­стем, которые содержат элементы со сравнительно высокой интенсивностью отказов  l _с  и когда эти элементы не подверже­ны переключениям во время нормальной работы системы.

Об экономичности системы, когда ее элементы включены без выполнения заданных функций, можно судить по эксплуатационным затратам за время   t.  Но более важным является тот факт, что в нагруженном  состоянии ( трубы заполнены водой)  большинство трубопроводов подвержено из­носу в меньшей степени, чем в состоянии простоя (не заполненных водой).

Стареющие элементы

 Очевидно, что трубы смонтированные и  уложенные в землю должны работать длительный срок без перекладки. Со временем они теряют свою работоспособность. Поэтому их целесообразно относить к стареющим элементам.

В теории надежности [2, 3, 6, 7, 23]  элемент называется стареющим, если с течением времени l ( t ) монотонно возрастает при t ₁ < t ₂, l ( t₁ ) £ l (  t ₂  ).  И если рассматривается случай со стареющим элементом (системой) то говорят: стареющая величина t , стареющее распреде­ление   F ( t ). Для стареющего элемента характерно, что его функция L ( t ) = 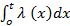выпукла вниз. В частности, стареющим является показательное распределение.

  Большинство распределений, используемых в теории на­дежности, ближе к моделям стареющих величин. И это не случайно.

Предположение о том, что элемент - стареющий, весьма есте­ственно. Физически - оно означает, что с течением времени эле­мент становится все менее и менее надежным. Если не учитывать периоды испытаний (приработки) , то практически все элементы водопроводных систем можно отнести к стареющим.

    Обычно конструкция системы такова, что время жизни системы t есть некоторая функция от времен жизни элементов t _1, t _{2, · · ·} , t _{n .}  Предположим еще, что элементы отказываю независимо друг от друга, то есть t _1, t _{2, · · ·} , t _{n . -}  неза­висимы.  Тогда система, составленная из стареющих элементов, как правило, сама будет стареющей [2, 23]. В теории надежности искомые характеристики надежности часто не находятся в явном виде из-за того, что сложна зада­ча, либо потому, что отсутствует необходимая информация. В этом случае естественно искать односторонние или двусторонние оцен­ки для этих характеристик. Чтобы понять, какие оценки нам нуж­ны, введем понятия положительной и отрицательной характерис­тики надежности. Характеристику назовем положительной, если ее увеличение соответствует увеличению надежности. Таковы ха­рактеристики P( t ) и  Т .

Наоборот, интенсивностьl ( t) является отрицатель­ной характеристикой, так как ее увеличение соответствует па­дению надежности. Пусть a - положительная характеристика. Тогда оценку вида a £ 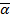 назовем оптимистической, а оценку вида a ³  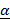пессимистической.            

 Оптимистические оценки завышают надежность, а пессимистические занижают ее. Ясно, что для прогноза надеж­ности нам нужны в основном пессимистические оценки [23]. Если най­дена такая оценка, то, конечно, полезно дополнительно иметь   оценку с другой стороны - она даст возможность оценить пог­решность пессимистической оценки.

Основной смысл теории стареющих элементов состоит в том, что в классе стареющих элементов можно получить большое число важных и простых оценок. В этом классе показательное распреде­ление является в некотором смысле экстремальным.