Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Вопросы формирования показателей надежности

Нормирование и выбор показателей надежности различных технических устройств, к каким относятся объекты водоснабжения (системы, сооружения, оборудование) необходимо выполнять с учетом рекомендаций, изложенных  в стандартизированных методических указаниях [ 6, 7, 8, 10 ]  .  

Нормирование надежности  объектов водоснабжения  ставится как неотложная технико-экономическая задача для оптимизации подачи и распределения воды потребителям [ 16, 19, 20, 21].  Нормы  надежности водопроводных сооружений, систем, получен­ные экспертным путем или с помощью методов технико-эконо­мической оптимизации, должны использоваться не только  на стадии их проектирования, но и эксплуатации. Обоснование надежности объектов водоснабжения в настоящее время осуществляется на экспертном уровне, поэтому с научной точки зрения, объективно не могут быть признаны как правомерными.

 Проблемы нормирования и обеспечения  надежности объектов водоснабжения обусловливают необходимость решения задач по расчету показателей их надежности.

Расчеты надежности и оптимальности  любых технических объектов строго регламентированы во всех странах мира. Поэтому инженерам, занимающихся данными расчетами, необходимо знать методы и правила их выполнения.

 Выбор методов расчета  надежности объектов водоснабжения обусловлен следующими особенностями:

- отсутствием регламентированной статистической информации о надежности сооружений и оборудования (объектов);

- сложностью натурных испытаний на надеж­ность объектов по  техническим и экономи­ческим причинам;

- ограничением данных  испытаний на надеж­ность объектов, поставляемых из различных стран мира; 

 - разнообразием и множеством факторов (случайных и детерминированных) , влияющих на надежность объектов;

 При оценке и расчете уровня надежности объекта необходимо  учитывать  факторы:    

- условия функционирования объекта;

- условия эксплуатации и квалификацию обслуживающего персонала (организацию работ, обеспечение запасными частями, техникой, профессиональный отбор, образование, дисциплина и др.);

- качество статистических данных;

- качество и периодичность ремонтов (плановых, внеплановых, аварийных );

- условия ведения отчетной документации по эксплуатации объектов  (данные о наработках, простоях, ремонтах, и испытаниях);

- соответствие используемой математической модели надежности натуре.

 Выбор  и обоснование  уровня надежно­сти объекта  связаны с показателями:

- удельного ущерба от возникновения отказа;

-уровня цен и системы ценообразования;

-ущерб общества, который возникает при прекращении подачи воды.

Следует отметить, что перечисленные выше факторы и показатели настолько сложно оценить и учесть, что на практике во всех странах мира инженеры отказались обосновывать уровни надежности объектов, к каким относятся объекты водоснабжения, экономическими методами. Оптимальность уровня надежности объекта назначается либо волевым способом либо по результатам сопоставления показателей надежности лучших аналогов. Но, к сожалению, в отечественной практике, оценок показателей надежности действующих объектов водоснабжения чрезвычайно мало. Практически нет выбора. Необходимо этот факт осознать, организовать работы по накоплению необходимой информации для достижения поставленной цели по нормированию и оценке надежности объектов водоснабжения.

       В теории надежности  распространено использование показателя Р( t ) - вероятности безотказной работы до момента t  или функции надежности и показателя  F (t) - вероятности наступления отказа за время t.   Эти показатели взаимосвязаны по условию  Р ( t ) = 1- F (t) = Р (Т > t ). Обычно предполагается, что распределение величины  Т  – непрерывное, т.е. существует плотность 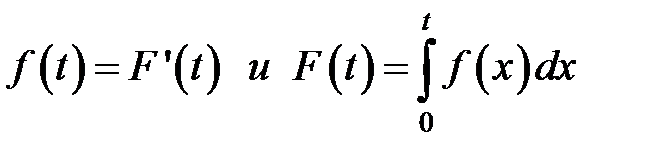.   Графики функций  Р ( t )  и F (t)  имеют вид:

t

P ( t )

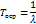
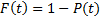
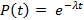
0,632

0,368

1 , 0

0

Рис. 2.1. Графики вероятностей Р ( t ) и F (t)    при экспоненциальном законе распределения непрерывной случайной величины t

           

       Во взаимосвязи с ними интенсивность отка­за объекта  определяется по зависимости: 

l(t)= 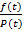 = 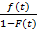,             (2.1)

       где f ( t ) –плотность распределения времени безотказной работы;

         Р( t )- вероятность безотказной работы;

         F ( t ) - вероятность наступления отказа.

       Другими словами, интенсивность отказа есть вероятность отказа объекта за единицу времени (если эта единица мала) при условии, что к данному моменту объект не отказал. Интегрируя (2.1), можно получить  выражение функции надежности через интенсивность отказа

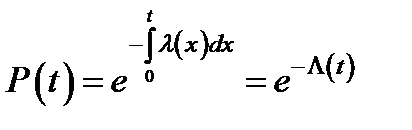,         (2.2)

       где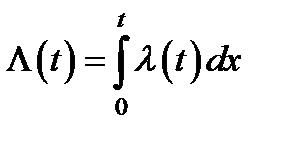

       Из (2.2) следует  выражение для вероятности безотказной работы объекта до момента t ₂ при условии, что к моменту t ₁ , он еще не отказал:

,

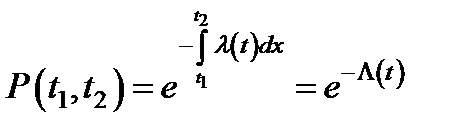       т.е. поведение объекта определяется значениями интенсивности только на  интервале ( t ₁ , t ₂).

Числовые характеристики.

       Функциональные характеристики надежности Р(t), l (t), f (t) , F(t) являются полными характеристиками, то есть содержат всю информацию о надежности объекта, (до пер­вого отказа). Однако на практике нам удобнее задавать надеж­ность числовыми характеристиками. Оценка числовых величин ста­тистическими методами требует меньшего объема испытаний, чем оценка функции распределения и тем более плотности распреде­ления. С другой стороны, потери от отказов при массовой эксп­луатации однотипных объектов обычно выражаются через некоторые средние характеристики надежности, и в этом случае функцию распределения отказа мы можем не знать. Наиболее важной числовой характеристикой надежности являет­ся среднее время безотказной работы или среднее время жизни объекта 

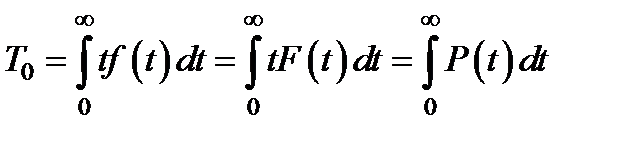                        (2.3)

(последний интеграл получается из предыдущего интегрированием по частям). Геометрически (см.рис. 2.1) среднее время есть пло­щадь под графиком функции надежности.

Наряду с этой характеристикой рассматривается и среднее время восстановления объекта  -  Т_в º t .

 Не редко  для оценки интервальной надежности объекта, функция безотказной работы которого имеет экспоненциальный закон распределения,  используется - коэффициент готовности  К_г,   т.е. вероятность того, что в   момент времени  t  объект находится в работоспособном состоянии и   проработает безотказно в течение интервала времени D t = t :

   

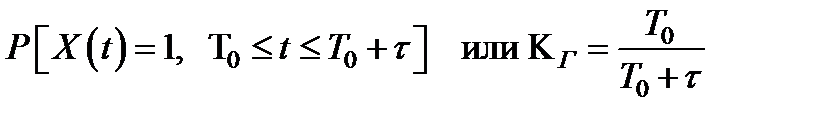
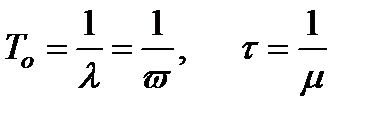                                       ,                       (2.4)

где Т_о – среднее время безотказной работы;

t - среднее время восстановления.

 l - интенсивность отказа;

v- параметр потока отказов;

m - интенсивность восстановления.

       Другой числовой характеристикой является дисперсия времени жизни

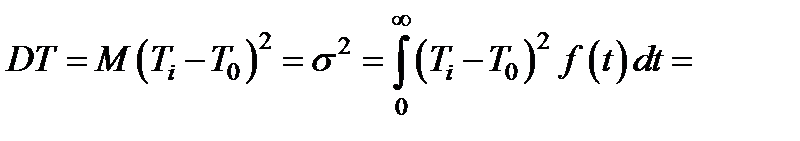
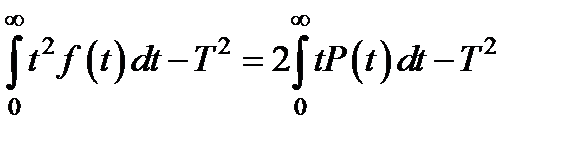=      (2.5)

f( t )

t

T

Рис.2.2 . Интерпретация понятия "дисперсии"

Величина = 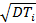дает нам среднее отклонение слу­чайного времени жизни T_i от своего среднего T_o   (см. рис. 2.2.)  Эта характеристика используется сравнительно редко - обычно для тех распределений, у которых плотность имеет резко выраженный одновершинный вид, т.е. разброс  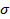 значительно меньше, чем среднее Т_о.

Иногда объект  рассчитан на выполнение одной задачи, которую он решает самостоятельно или в составе некоторой системы. После выполнения этой задачи объект не используется, например, уничтожается. Если задача решается за время t _о  то в этом случае нас интересует не  вся функция надежности , а только ее значение  G = Р(t _о)    

       Часто время выполнения задачи t_z   - случайное. Пусть F ( t )= P ( t_z < t )- функция распределения времени выполнения задачи. Предположим, что задача выполняется тогда и только тогда, когда во время ее решения элемент не отказывает. В этом случае вероятность выполнения задачи равна

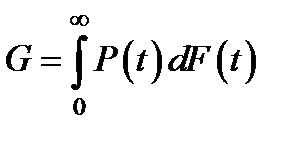        (2.6)

       Опыт показывает, что даже хорошо изготовленные и  правильно эксплуатируемые объекты (оборудование, сооружения и системы) не могут быть полностью гарантированы от возникновения отказов.  Причем, возникновение отказов во времени  под­чиняется определенной закономерности (см. рис. 2.3),  которую  можно проследить по изменению интенсивности отказа  l ( t ): повышен­ное значение интенсивности отказа в начальный период эксплуа­тации, затем наблюдается спад и стабилизация кривой на относи­тельно низком уровне и новый рост интенсивности отказа, не пре­кращающийся вплоть до окончания эксплуатации. 

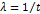
Износовые  отказы

Период нормальной эксплуатации

Период износа

Внезапные и износовые отказы

Прира-боточные отказы

Период приработ-ки

Время эксплуатации Т

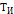
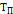
0

М

Интенсивность отказов

 

Рис. 2.3. Интенсивность отказа объекта как функция времени эксплуатации (долговечности)

       По характеру поведения l (t) вся ось времени может быть разбита на три участка.    На первом участке возникают отказы,    которые происходят в течение раннего периода эксплуатации объекта. Они называются приработочными отказами и в большинстве случаев происходят вследствие плохой технологии монтажа и плохого контроля качества объекта при его строительстве. Подобные погрешности не вызывают беспокойства, и отказы, к которым они неизбежно приводят, случаются обычно в течение первых минут или часов работы. Ранние отказы могут быть исключены так называемыми процессами   «приработки». Процесс приработки состоит в том, что объект в течение нескольких часов заставляют работать в условиях, близких к условиям эксплуатации; дефектные, составные части объекта, отказывающие в течение этих первых часов работы объекта, заменяют исправным оборудованием, конструкциями; если выявляются дефекты или какая-либо ошибка монтажа, они исправляются. Только после этого объект сдается в эксплуатацию потребителям.

На втором участке возникают  отказы, которые вызываются износом составных частей (деталей насосов, двигателей, запорной арматуры, труб и т.д.) объекта. Они возникают у объекта, который  неправильно обслуживается или совсем не обслуживается. Отказы за счет износа являются признаком старения объекта. Период износа составных частей объекта (деталей насосов, двигателей, запорной арматуры, труб) колеблется от нескольких минут до нескольких лет. В большинстве случаев отказы за счет износа могут быть предотвращены. Например, для многократно используемого объекта одним из возможных методов является замена через определенное время его составных частей, которые подвержены износу, причем интервал времени между заменами должен быть короче среднего периода его износа. Если доступ к отдельным частям объекта (например, дюкерам, переходам трубопроводов) затруднен, то они рассчитываются на более длительный срок службы, чем предполагаемый (нормируемый) период работы объекта.  Перед пуском в эксплуатацию подобные объекты (изделия) предварительно испытываются и включаются в работу  с момента Т_п.  У  многих правильно спроектированных и смонтированных  объектов водоснабжения период старения на­ступает через существенный  промежуток времени ( 1 £ t £ 50 лет). В этой связи,  реальный  срок их  службы    укладывается на втором периоде,    а интенсивность отказов стабилизируется  l(t)=const.

На третьем участке возникают  так называемые внезапные отказы, которые не могут быть устранены ни при испытаниях, ни в процессе эксплуатации. Такие отказы возникают вследствие внезапной концентрации нагрузок, превышающей расчетную нагрузку. Внезапные отказы возникают случайно, неожиданно; никто не может предсказать, когда они произойдут. Однако такие внезапные отказы все же подчиняются определенным общим закономерностям, так что частота отказов в течение достаточно большого периода примерно постоянна. Внезапные отказы называют иногда «катастрофическими», однако это название неточно, так как приработочные и износовые отказы могут быть столь же «катастрофичными»  по своим последствиям, а внезапные отказы не обязательно  должны быть «катастрофичны» для объекта, в котором они происходят.

 Классификация отказов на приработочные, износовые и внезапные производится по двум основным признакам. Во-первых, каждый из этих типов отказов характеризуется своим особым статистическим распределением и поэтому требует различной математической обработки. Во-вторых, для устранения каждого типа отказов должны применяться различные методы.

 Первоочередная задача  обеспечения надежности состоит в исключении сначала приработочных отказов посредством наблюдения их распределения и определения в соответствии с этим необходимой длительности периода приработки и последующих мер доводки объекта. Предупреждение износовых отказов осуществляется за счет мероприятий по выявлению причин  таких отказов, определения межремонтных сроков и сроков профилактической замены различных деталей, оборудования. Наконец, главное внимание должно быть обращено на внезапные отказы: на их предупреждение, уменьшение или полное устранение, потому что именно внезапный отказ наиболее пагубно сказывается на надежности оборудования, сооружения, объекта во время основной работы — в период после испытания объекта и перед началом износа его частей. Для объектов с большим сроком службы (50 и более лет) это время соответствует периоду между ремонтами.

К сожалению, часто даже всех приложенных усилий оказывается недостаточно для полного исключения приработочных и предупреждения износовых отказов. Приработочные отказы могут вкрасться в объект (деталь оборудования, конструкцию сооружения) при каждом осмотре или ремонте в результате неправильного выбора деталей для замены отказавших или приближающихся к состоянию износа объектов, вследствие ошибок монтажа или в результате не вполне удовлетворительной наладки системы, производимой при ремонте. Такой негодный ремонт может привести к приработочным отказам объекта в течение всего времени функционирования; объект при этом никогда не будет надежным, хотя при хорошем ремонте и при учете только внезапных отказов объект мог бы представлять собой весьма надежное техническое устройство. Подобным же образом износовые отказы могут быть  причиной существенного падения уровня надежности  любого объекта. Однако увеличение интенсивности отказов объекта, как правило, является следствием нарушений  эксплуатации,  а не скрытых изъянов конструкции, схемных решений его компоновки.

       Высокая надежность – это низкая интенсивность отказов l и, следовательно, большая средняя наработка на  отказ Т_о . Понять вероятностный смысл характеристики l можно на таком примере.

       Допустим,  на объекте для понижения грунтовых вод  установлено 100 погружных насосов в скважинах, которые эксплуатируются без восстановления, и с течением времени отказывают. Рабочих скважин – 30 шт., остальные резервные. Насосы однотипные и включаются в работу и отключаются  по усмотрению диспетчера (по случайному принципу), с одинаковым коэффициентом использования k _и.

       За первые 5 лет эксплуатации отказало 50 насосов, а за последующие 5 лет отказало 20 насосов. Спрашивается, когда насосная установка наиболее надежна  в начальный момент или через 5 лет с момента эксплуатации. На первый взгляд,  кажется, что  в начальный момент  установка  была менее надежна,  так как за 5 лет отказало 50 погружных насосов, а на втором интервале  через  5 лет отказало только 20 насосов.  Но такие рассуждения неправильны. Ведь в начальный момент на объекте было 100 насосов и за 5 лет отказал каждый второй , а на последующем этапе  осталось только 50 насосов и за 5 лет отказал каждый 2,5 -й  насос. Таким образом, за локальную характеристику надежности в момент t =t_o +5 лет   выполнив оценки показателя интенсивности отказов: l₁= 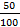 = 0,2  и l ₂ =  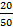=0,4 ,  мы придем к противоположному выводу , так как l ₁ < l ₂ .

                      

 2.3. Законы надежности

       Оценка функции надежности Р( t )  статистическими методами  требует большого объема информации , которая формируется за счет отчетных данных либо данных испытаний объекта.  В теории математической статистики [ 5] данные наблюдений или данные эксперимента в принципе не влияют на выбор методов получения научно обоснованных выводов о массовых явлениях. Названия источников получения информации обезличиваются, а потому именуются как данные испытаний.  Кроме того, испытания   объекта на заданном участке времени всегда  имеют ограничения по тем или иным причинам, и  мы не можем в принципе ничего сказать  о надежности объекта за пределами  этого участка времени, т.е.   не можем экстраполировать надежность. Положение в корне меняется  тогда, когда мы знаем вид функции надежности с точностью  до одного или нескольких неизвестных параметров Р( t )= Р( t , a , b …).Оценка этих параметров требует значительно меньшего объема испытаний. Кроме того, оценив параметры надежности на всем бесконечном интервале времени (если , конечно,  мы уверены, что вид распределения не меняется на всей оси).

       Тип распределения можно найти двумя путями - статистически, проверяя гипотезу о принадлежности нашего распределения данному типу, и физически, построив физическую модель отказа и исследовав ее математическими методами.

     Первый метод обладает тем же дефектом, что и вообще статис­тическая оценка распределения - если, проводя испытания на дан­ном интервале времени, мы, пусть даже с высоким уровнем значи­мости, подтвердили гипотезу о принадлежности распределения дан­ному типу, то отсюда не следует, что этот тип распределения сохраняется за пределами этого интервала.

Второй метод требует обширной и глубокой информации (часто на микроуровне), которой почти никогда у нас нет. Тем не менее, несмотря на эти пессимистические соображения, в теории и прак­тике надежности используется несколько типов распределений, с которыми мы сейчас познакомимся.

 

  2.3.1.Экспоненциальный (показательный) закон.

Так называют распределение вида

Р ( t ) = 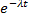            (2.7)

Для  него

F(t)=1- 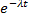, f(t)= l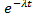              

Интенсивность отказа 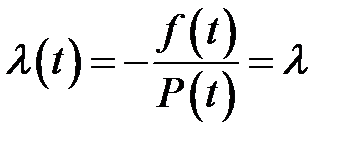 постоянна.  Среднее время жизни

.

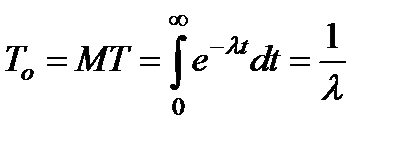       Поэтому экспоненциальный закон часто записывают в виде:

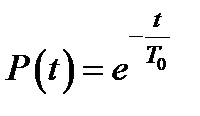                  (2.8)

       Дисперсия, как нетрудно подсчитать, равна:

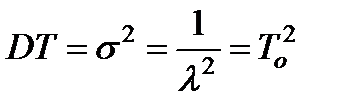,     (2.9)

то есть дисперсия равна квадрату среднего. Этот факт можно использовать для статистического подтверждения экспоненциаль­ного закона, поскольку моменты MT = MT ²     - статисти­чески оцениваются очень просто. Если время t  мало, то есть t < T_o  , то можно пользоваться приближенной формулой

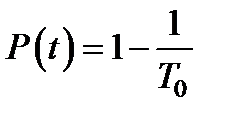 ,        (2.10)

в которой ошибка не превосходит 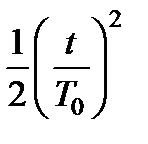. Для экспоненциального характерно, что  вероятность безотказной работы в течение времени t не зависит от того, сколько времени до этого проработал объект.   На этом свойстве основано применение в теории надежности марковских процессов.

        Экспоненциальный закон чрезвычайно популярен в теории надежности. В большинстве работ, особенно там, где решаются сравнительно сложные задачи, предполагается без какого - либо обоснования, что функция надежности показательная.

При этом обычно приводятся такие доводы: а) все так делают, б) если не предполагать показательности, то задача не решает­ся, в) даже если истинная функция надежности не показательная, то все равно использование показательного распределения дает неплохое приближение, г) у нас обычно имеется очень небольшая статистическая информация о распределении отказами в этих ус­ловиях естественно использовать показательный закон как самый простой однопараметрический закон.

Ясно, что первые два довода не являются убедительными. Ниже в главе 3 будут изложены методы, позволяющие решать даже трудные задачи при произвольных предположениях относительно распределе­ний. Что касается третьего довода, то тут все зависит от типа задачи - для некоторых задач замена произвольного распределения показательным не сильно меняет характеристики (порядок величин сохраняется), но в других задачах от таких действий характе­ристики могут увеличиваться или уменьшаться в 10-100-1000 раз. Наконец, последний довод также не выдерживает критики - исполь­зование показательного закона существенно искажает статистиче­скую информацию.

У многих объектов водоснабжения период старения наступает через большой промежуток времени, так что реальный срок службы объекта укладывается в нормальный период (см. рис. 2.3). На данном участке работы  l ( t ) º const, и в этом случае при расчете надежности пользоваться показательным законом.

Таково статистическое обоснование правильности использования показательного закона.

Следует, однако, иметь в виду, что при такой статистической проверке показательности распределения необходимо соблюдение двух условий:

а) объем наблюдений должен быть достаточно велик - не менее нескольких сотен наблюдений (испытаний);

б) если испытания проводились на некотором участке времени, то и подтвердить показательность распределения мы можем только на этом участке. Утверждать, что интенсивность постоянна вне данного участка, мы не можем, как бы ни был велик объем испытаний.  

В некоторых ситуациях мы можем физически проверить равенство (2.8), из которого следует показательность распределения.   

Рассмотрим сложную систему, со­стоящую из большого числа элементов. В момент отказа каждый элемент заменяется новым. Если наша система не обладает избы­точностью, то каждый отказ элемента является отказом системы. Таким образом, поток отказов системы есть сумма большого числа потоков отказов элементов. В теории потоков доказывается (тео­рема Хинчина) , что сумма большого числа независимых по­токов будет с большой точностью потоком пуассоновским.      Важным свойством этого потока является то, что  время от данного момента до ближайшей точки (отказа) этого потока имеет показательное распределение.

Итак, если система состоит из большого числа элементов, то время до первого отказа с хорошим приближением имеет экспоненциальное распределение.

  Используя это распределение в задачах надежности, необходимо каждый раз проверять законность та­кого шага.

 

 

 2.3.2. Нормальный закон

Строго говоря, в  теории надежности используется усеченный нормальный закон.

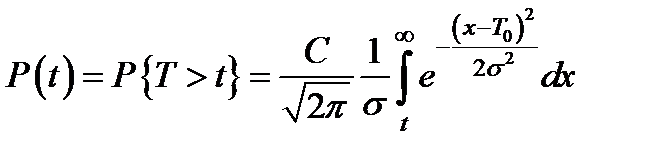 ,  (2.11)

где множитель С находится из условия Р (0) = 1.

Но посколь­ку в задачах теории надежности обычно среднеквадратический разброс  гораздо меньше, чем среднее время жизни  Т _o , 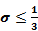Т _o, то можно принять, что С  = 1.

Интенсивность отказа для нормального закона имеет следующий вид:

 

f(t)

λ(t)

P(t)

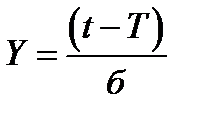
T

P(t)

λ(t)

f(t)

Время эксплуатации Т, часы

1

0,5

Рис. 2.4. Интенсивность отказов при нормальном распределении

Кривая выходит из начала координат и, монотонно возрастая, при­ближается к асимптоте Y =(t - T ) / 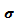. Нормальное распределение имеет ту особенность, что площадь под кривой плотности становится равной 100% только в том случае, когда кривая в обоих направлениях простирается до бесконечности. Однако это принципиально невозможно, потому что новые изделия (элементы) включаются в работу в момент Т=0, а не в момент Т = - ¥. Нормальное распределение может, следовательно, рассматриваться только как аппроксимация. Однако эта аппроксимация, как правило, оказывается очень точной, особенно в тех случая, когда стандартное отклонение мало по сравнению со средней Т_о.

Выше отмечалось, что все отказы делятся на внезапные, которые имеют чисто случайный характер, и постепенные, которые возникают в результате постепенного старения, износа элемента. Условно предполагается, что внезапные отказы подчиняются показательному закону, а постепенные  - нормальному. Эта условность обусловлена тем, что   строгого  определения внезапных и постепенных отказов не существует, которое бы позволило отличать их друг от друга.

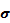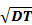
 Обычно нормальный закон можно использовать (и притом с не­плохой точностью), если плотность  f ( t) имеет одновершин­ный симметричный вид и =  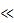MT = T_o

  

 2.3.3. Нормально-экспоненциальный закон.

       Данный закон позволяет отразить появление внезапных и изнозовых отказов при функционировании объекта. При его выводе использовались в большей мере аналитические методы [10, 15, 23 ]. Предполагалось,  что объект состоит как бы из двух частей, од­на из которых отказывает по экспоненциальному закону

P { T ₁ > t } = ,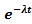

а другая отказывает независимо от первой по нормальному закону 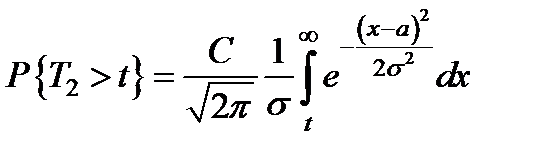    ,            (2.12)

где а = МТ₂ – случайный параметр времени, который имеет нормальный закон распределения.

       Отказ объекта  наступает тогда, когда отказывает хотя бы одна из его частей, то есть

Т = min ( T _1, T ₂ ),

       тогда

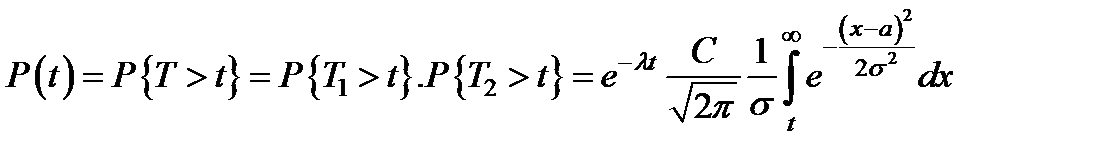
       С учетом данной модели, можно определить среднее время жизни объекта, предполагая, что 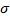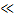а,

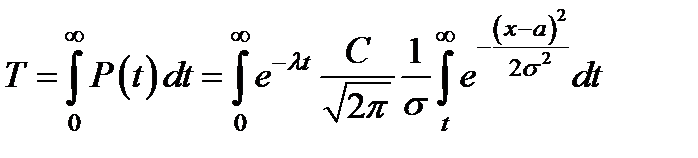
       Если поменять порядок интегрирования, то в окончательном  виде получим:

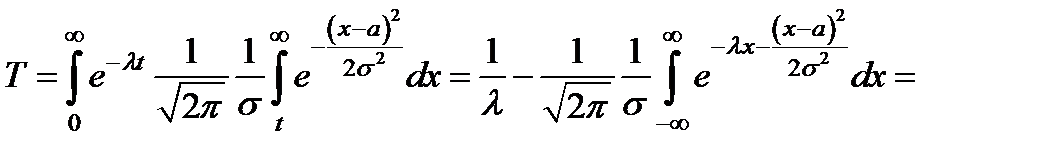
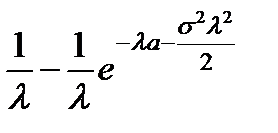=             (2.13)

 

Закон Вейбулла

       Функция распределения Вейбулла имеет вид

F ( t ) = 1- 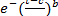 ,                (2.14)

       где а, b , с- параметры распределения , которые должны удовлетворять условию а 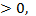b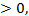

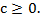
Параметр а - является характеристикой масштаба, b – характеристикой формы, с - характеристикой сдвига.

       Плотность вероятности распределения Вейбулла имеет вид

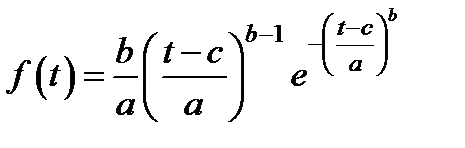                       (2.15)

       при условии t ³ c , f ( t =0 и t < c .

       Если Т  является наработкой до отказа, то вероятность безотказной работы до наработки t  находится по уравнению

Р(t) = 1-F(t) = 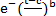,                         (2.16)

а интенсивность отказов по уравнению

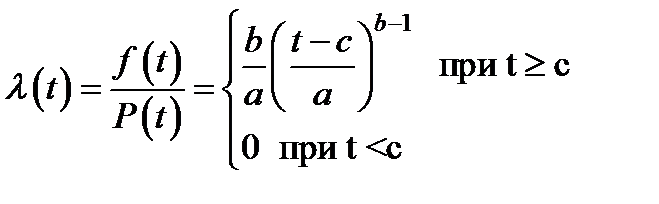(2.17)

Для расчетов по уравнениям (2.14 , 2.15) можно пользоваться  стандартными таблицами [ 9,11].

Распределение Вейбулла широко используется в теории надеж­ности.   Конечно, предположение о степенном характере функции распределения в окрестности нуля довольно естественно, но ниоткуда не следует, что показа­тель  у всех функций будет один и тот же. Если же показа­тели разные, то никакого закона Вейбулла не получится.

       Однако в пользу распределения Вейбулла есть один сущест­венный довод. Распределение Вейбулла есть двухпараметрическое распределение, которое содержит в себе показательное распреде­ление . Поэтому любое реальное распределение приближается распределением Вейбулла заведомо намного лучше, чем показательным распределением. Это соображение в значитель­ной степени оправдывает применение закона Вейбулла.

Гамма-распределение.

       Гамма-распределение определяется двухпараметрической плотностью вероятност,

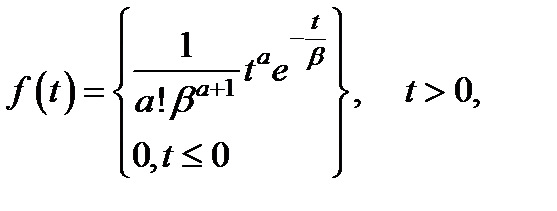  (2.18)

причем параметр масштаба b > 0 и параметр формы а > -1

       Функция распределения

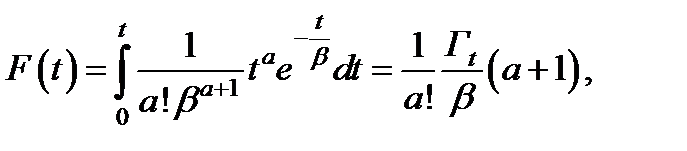(2.19)

       Функция надежности

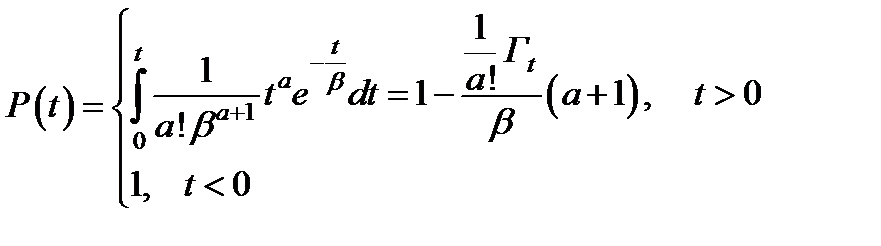 ,  t 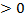, (2.20)

         Неполную гамма-функцию очень трудно рассчитать; однако если а – целое число, то

P(t) = 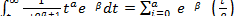ⁱ  =

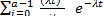
       В этом случае время T можно интерпретировать , как сумму независимых слагаемых

Т= x ₁ + x ₂ + x ₃ + …. x _{a ,}                                             (2.21)

       где каждое слагаемое имеет показательное распределение

Р =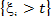

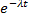
       Среднее значение и дисперсия находятся из уравнений:

МТ=  , DT =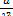

       Для расчетов по уравнениям (2.18) – (2.19) можно пользоваться таблицами, приведенными в [ 15]

       Поскольку гамма-распределение содержит в себе показательное (а=1) , в его пользу можно привести те же доводы, что и для распределения Вейбулла.

       Гамма-распределение имеет   преобразование Лапласа  

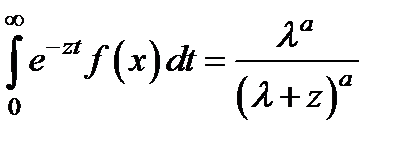
и поэтому его удобно использовать в тех задачах, где решение находится в терминах преобразования Лапласа.  При целом a = n  выражение  (2.19) дает возможность исполь­зовать марковские методы в тех моделях, где все исходные рас­пределения являются гамма-распределениями.

ГЛАВА НАДЕЖНОСТЬ СИСТЕМЫ