Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотренные выше законы распределения наиболее полно характеризуют случайные величины, так как указывают, какие значения (или из каких интер­валов) может принимать соответствующая случайная величина и каковы вероят­ности этих значений. Однако в ряде случаев для выполнения инженерных расчётов о случайной величине требуется знать гораздо меньше, а именно:

1). Знать   некоторое среднее  из значений случайной величины, вокруг которого группируются остальные значения, т. е. знать положение «центра группирования» на числовой оси;     

2). Знать  каково рассеивание массы вероятности относительно неко­торого центра, т. е. знать числовую характеристику рассеивания.

 Наиболее часто употребляются в технике следующие числовые характери­стики положения центра группирования:

- математическое ожидание или среднее значение случайной величины Т обозначаемое символом M Т;

- медиана случайной величины t, обозначаемая символом М_еt;

- мода случайной величины t, обозначаемая символом М_оt.

- квантиль , отвечающая заданному уровню вероятности Р, называют такое значение x = x_p , при котором   функция распределения принимает значение Р, т.е. F(x_p)= P.

 Рассмотрим оценку  математического  ожидания или среднего  значения .

 Среднее значение случайной непрерывной  величины представляет собой на­чальный момент первого порядка то есть

      = М [ T ]                        (1.30)

Математическое ожидание не является случайной величиной, оно принимает вполне определенное значение и определяется по формуле:

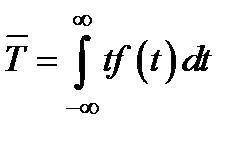                            (1.31)

Статистическое значение средней величины определяется из соотношения:

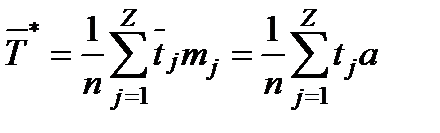       (1.32)

Величина 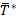, определяемая  по формуле (1.12) является несмещенной, состоятельной и эффективной оценкой математического ожидания M[Т].  

Величина 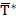   случайна и являет­ся функцией объема результатов наблюдений.

Под понятием медиана Меt в математической статистике подразумевается квантиль, которая отвечает значению F(t_p) = p =  , т.е. такое значение, для которого функция распределения равна .  При геометрической интерпретации (см. рис. 1.4  )  -  медиана есть абсцисса такой точки кривой плотности вероятности f(t), ордината которой делит площадь под кривой на две равные части.

f(t)

t

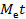
F1

F2

 

 

Рис.1.4. Интерпретация понятия "медиана"

В математической статистике модой М_о t называется наиболее вероятное значение t_i случайной непрерывной величины Т , плотность вероятности f(t) которой имеет наибольшее значение. ( см. рис. рис.1.5).

f(t)

t

 

 

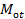
Рис. 1.5. Интерпретация понятия "мода"

  Не менее важной характеристикой случайной величины служит ее показатель рассеивания.  Например, если   имеются  две равномерно распределенные непрерывные случайные величины и одна из них распределена в области от- 5 до +5, а другая — от -500 до  +500, то эти величины  имеют одинаковые математические ожидания, но существенно различаются по характеру рассеивания. Первая из них  компактнее распределена относительно средней, чем вторая. Характеристика, показывающая насколько тесно сгруппированы воз­можные значения случайной величины около центра группирования, называется числовой характеристикой рассеивания. Очевидно, что таких характеристик с оди­наковым назначением может быть несколько.

В технике наиболее часто употребляются следующие характеристики рас­сеивания:

- дисперсия, обозначаемая символом DТ (или DХ),

- среднее квадратическое отклонение, обозначаемое через s _t

- коэффициент вариации, обозначаемый символом J_t

 Во всех этих характеристиках за центр рассеивания принимается математи­ческое ожидание величины.

 Формулы для определения дисперсий    имеют вид:

для дискретных величин

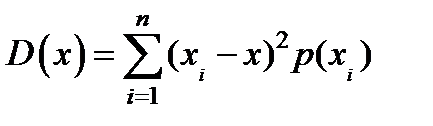    (1.33)

для непрерывных величин

                             

 

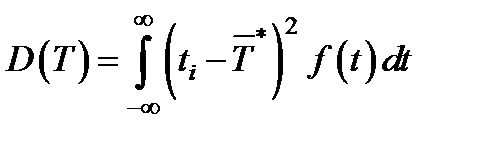
Характеристики рассеивания случайной величины графически может быть представлена в виде  (см. рис. 1.6):

f( t )

t

 

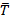
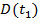
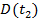
Рис. 1.6. Интерпретация понятия "рассеивание случайных величин"

Cтатистическая  дисперсия 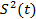, характеризующая рассеивание случайной величины  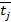   в наблюдениях объемом n  определяется по формуле:

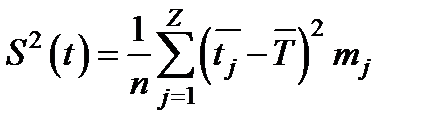               (1.34)

где 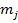 - число наблюдений в j -м интервале;

z- количество интервалов, на которое разбиваются все наблюдения;

или

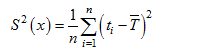(1.35)

Здесь в качестве средней величина 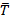 используется ее теоре­тическое значение. На практике эта величина практически не известна, поэ­тому используется ее оценка  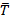* определяемся по результатам наблюдений. В этих случаях при обработке статистических данных для определения 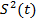используются формулы:

  (1.36)

или

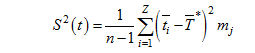(1.37)

 

В технике чаще пользуются не самой дисперсией, а корнем квадратным из нее, взятым с положительным знаком, называемым средним квадратическим отклонением и обозначаемым символом s ( t ).

Итак

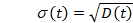                                 (1.38)

или при его оценке 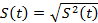                            (1.39)

Коэффициент вариации. В качестве относительной характеристики рассеивания используется еще коэффициент вариации, обозначаемый символом J _t , представляющий отношение среднего квадратического  отклонения к среднему значению Т или 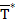 (см. рис. 1.7 ), т.е.

J _t = 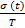(1.40)

или эмпирический коэффициент вариации

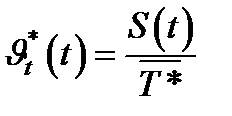                  (1.41)

i GA4Hq/PRZzscbOut8FIUR7OoQV7jdxuku1X9xgT9METzXjrZx1/CePN/AAAA//8DAFBLAwQUAAYA CAAAACEA40CfVuAAAAAJAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnBm90kJbaN 2ZRS1FMRbAXpbZudJqHZ2ZDdJum/dzzp8b03vPdNvp5sKwbsfeNIQTyLQCCVzjRUKfg6vD0tQfig yejWESq4oYd1cX+X68y4kT5x2IdKcAn5TCuoQ+gyKX1Zo9V+5jokzs6utzqw7Ctpej1yuW1lEkXP 0uqGeKHWHW5rLC/7q1XwPupxM49fh93lvL0dD+nH9y5GpR4fps0LiIBT+DuGX3xGh4KZTu5KxotW QZoweVCQxAsQnKfLiI0TG4vVHGSRy/8fFD8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA 4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEA OP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA XFFzDGsJAABRQwAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAA ACEA40CfVuAAAAAJAQAADwAAAAAAAAAAAAAAAADFCwAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAE AAQA8wAAANIMAAAAAA== ">

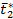
f( t )

t

 

 

 

  

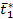
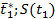
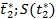
Рис. 1.7. Интерпретация  относительной характеристики рассеивания - "коэффициента вариации"

Корреляция между двумя событиями.  В инженерной практике случай применения коэффициента корреляции для оценки силы (тесноты) связи между величинами, когда исследуется связь между двумя признаками Х к Y, встречается сравнительно часто. Например, зависимость бесперебойной работы электроагрегата от частоты его включений  и возникающей при этом пусковой нагрузки по мощности. Такая зависимость общеизвестна и она оценивается всеми изготовителями и эксплуатирующими организациями насосных агрегатов, нагнетателей воздуха.

Коэффициентом корреляции величин Х и Y  называется ковариация cov( 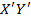) нормированных величин  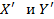. Этот коэффициент по абсолютной величине всегда меньше единицы и достигает значения +1 или   - 1 лишь при наличии точной линейной зависимости между величинами  Х и Y . В теории математической статистики [ 3, 13 ] коэффициент корреляции обозначают 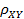. Ковариацией называют еще моментом связи случайных величин X и Y.

Вычисление коэффициента 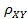 можно рассмотреть на примере.

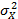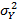Пусть X и Y - случайные величины с математическими ожиданиями М X , М Y   и дисперсиями и  . Величины X и Y нормированы, оценки которых получают по формулам:

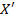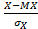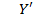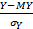= , = ,        (1.42) 

где 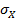 , 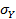- среднее квадратическое отклонение случайной величины Х от центра группирования МХ и соответственно Y от М Y .

Вычисления ковариации и коэффициента корреляции величин X и Y выполняется по формуле:

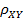= cov( 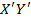) = М (  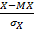· 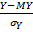)= = 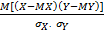= 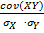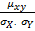,    (1.43)                                        

Если величины X и Y независимы, то их ковариация, а следовательно, и коэффициент корреляции равны нулю. Обратное заключение о независимости величин при условии 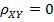 несправедливо.

Коэффициент ассиметри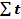и  ( или )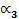

Он характеризует асимметрию кривой распределения f( t ) (см. рис. 1.8) и вычисляется как отношение третьего центрального момента 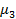 ко второму центральному моменту в степени 3/2; то есть

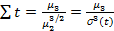               (1.44)

2 ja/2Dfdqn0Ecg1BjzeshxkC83OM5TlORw7zSRFkESMf5aeTmFHdtyDMG4nt0HeNbwerF6MFch3zh nyPR1+I62lVR4hq/1yASOuq3JfgPQrQ/C6B9/AWMd/8HAAD//wMAUEsDBBQABgAIAAAAIQAA6ibA 3gAAAAgBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8NAFITvgv9heYI3u0malBKzKaWopyLYCuLt NfuahGZ3Q3abpP/e50mPwwwz3xSb2XRipMG3ziqIFxEIspXTra0VfB5fn9YgfECrsXOWFNzIw6a8 vysw126yHzQeQi24xPocFTQh9LmUvmrIoF+4nix7ZzcYDCyHWuoBJy43nUyiaCUNtpYXGuxp11B1 OVyNgrcJp+0yfhn3l/Pu9n3M3r/2MSn1+DBvn0EEmsNfGH7xGR1KZjq5q9VedKzTLOOoAn7E9jpL VyBOCpZJkoIsC/n/QPkDAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAA AAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAA CwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAPo9GwpoJAABJQwAA DgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAAOomwN4AAAAI AQAADwAAAAAAAAAAAAAAAAD0CwAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAP8MAAAA AA== ">

f( t )

t

симметричное

асимметричное

 

Рис. 1.8. Интерпретация    характеристики  - "ассиметрия"

 

Статистическое значение коэффициента асимметрии определяется по формуле:

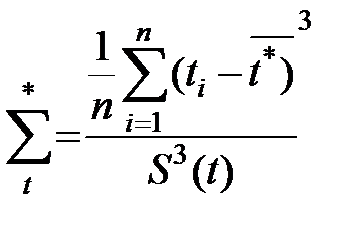                        (1.45)

 

Коэффициент эксцессса E_x ( или )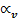

Он является показателем островершинности кривой распределения f(x) , то-есть характеризует насколько рассматриваемое распределе­ние отличается от нормального.

f(x)

x

Рассматриваемое распред.

Нормальное распред

 

 

Рис. 1.9. Интерпретация    показателя  - " коэффициент эксцесса "

 

Коэффициент эксцесса представляет собой отношение четвертого центрального момента 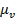 к квадрату второго центрального момен­та  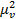то есть

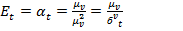(1.46)

Статистическое значение коэффициента эксцесса начисляется по формуле:

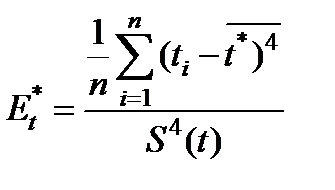           (1.47)

Понятие числовых характеристик может быть распространено и на систему случайных величин.

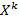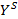Например, для двух случайных величин X и Y начальным моментом порядка k , S назы­вается математическое ожидание произведения и   т.е.

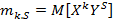           (1.48)

Центральный моментом порядка k , S систем (X,Y) назы­вается математическое ожидание произведения в k-ой и S-ой степени соответствующих центрированных величин 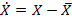 и 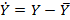, т.е.

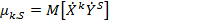(1.49)

Для дискретных величин выражения для этих моментов имеют вид:

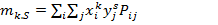(1.50)

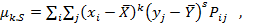(1.51)

где 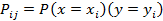. - вероятность того, что систѳма примет значение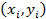

Для непрерывных величин формулы для 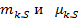прямут вид:

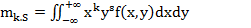(1.52)

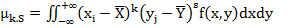(1.53)

Важное значение при решении ряда прикладных вопросов имеет второй смешанный центральный момент .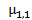

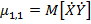
представяющий собой математическое ожидание произведения центрированных величин. В литературе  по теории вероятностей [5, 13 ]  его часто называют моментом связи, ковариацией, корреляционным моментов случайных величин X и Y.