Соответствие между всеми возможными значениями случайной величины и их вероятностями называется законом распределения данной случайной величины.
Как правило в качестве закона распределения случайной величины используется функция распределения ( интегральный закон распределения) случайной величины: Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е. F(x) = P {X < x}.
Иногда функцию F(x) называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами:
1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.
2. Функции распределения есть неубывающая функция.
3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
Р{а < X < b} = F(b) – F(а). ( 1.3.)
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b.
5.Справедливы следующие предельные отношения:
 На практике функции распределения непрерывных случайных величин именуют как законы распределения. Подобное допущение не искажает существенно точность при оценке случайных событий.
На практике функции распределения непрерывных случайных величин именуют как законы распределения. Подобное допущение не искажает существенно точность при оценке случайных событий.
В теории надежности водоснабжения в качестве основной непрерывной случайной величины рассматривается время t (время наработки на отказ, время восстановления и т.д.). Поэтому в дальнейшем все рассуждения о непрерывных случайных событиях будем проводить с учетом тождества X º t и условия
F ( t ) = P { T 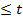 } ( 1.4)
} ( 1.4)
Следовательно, P { T 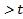 }=1- F ( t ) , поскольку рассматриваются противоположные события, которые образуются полную группу событий.
}=1- F ( t ) , поскольку рассматриваются противоположные события, которые образуются полную группу событий.
Для решения ряда задач необходимо знать теоретические законы распределения случайных величин.
Рассмотрим две группы законов распределения случайных величин:
- для дискретных случайных величин;
- для непрерывных случайных величин.
1.2.1. Законы распределения дискретных случайных величин
Для решения ряда задач необходимо знать теоретические законы распределения случайных величин.
Наиболее часто применяются следующие законы распределения дискретных величин:
I. Биноминальное распределение
Это распределение возникает в случае, если:
а) при испытаниях возможно два исхода: появление и не появление события;
б) испытания проводятся объемом n, установленном заранее;
в) при каждом испытании вероятность появления интересующего нас события остается постоянной.
Биноминальное распределение описывает распределение вероятностей 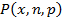 - вероятностей появления ровно х событий в испытаниях объема n с вероятностью р появления события в каждом испытании.
- вероятностей появления ровно х событий в испытаниях объема n с вероятностью р появления события в каждом испытании.
Интересующая нас вероятность появление ровно х событий в испытаниях объемом n определяется по формуле:
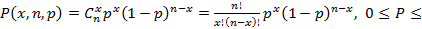 1. (1.5)
1. (1.5)
Здесь величины n и p являются параметрами закона распределения.
Переменные величины, определяющие значения искомой вероятности, называются параметрами этого распределения.
Числовые характеристики биномиального распределения (точное определение которых будет приведено ниже в разделе 1.3) и их связь с параметрами распределения могут быть представленны в виде:
- математическое ожидание представляем собой число событий, возникающих при многократном повторении испытаний
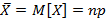 (1.6)
(1.6)
- дисперсия
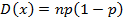 (1.7)
(1.7)
- коэффициент вариаций
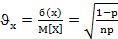 (1.8)
(1.8)
- коэффициент ассиметрии
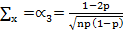 (1.9)
(1.9)
- коэффициент эксцесса
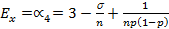 (1.10)
(1.10)
Отметим, что для нормального распределения 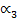
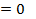 и
и 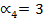 .
.
Часто необходимо знать статистические значения величия 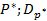 . Значение
. Значение 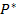 можно оценить по формуле:
можно оценить по формуле:
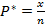 (1.11)
(1.11)
где х - количество интервесующих нас исходов испытаний;
n- общее число испытаний.
Математическое ожидание этой оценки
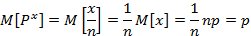
Таким образом, статистическое значение вероятности 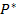 , определенное по формуле (1.11), является несмещенной оценкой р;
, определенное по формуле (1.11), является несмещенной оценкой р;
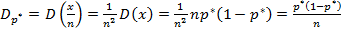 (1.12)
(1.12)
Следовательно,
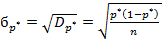 (1.13)
(1.13)
Если объем наблюдений n увеличивается 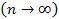 , то биномиальное распределение стремится к нормальному с параметрами;
, то биномиальное распределение стремится к нормальному с параметрами;
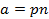
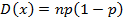
Функция распределения для биномиального закона
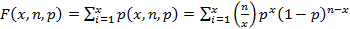 (1.14)
(1.14)
Пример.
Определить вероятность того, что в контролируемой партии оборудования будет обнаружено число бракованных штук более двух но менее или равно 4, для случая, когда:
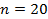 ;
; 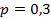
Таблица 1.1.
Данные к примеру

| 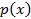
| 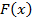
|
| 0 | 0,0008 | 0,0008 |
| 1 | 0,0068 | 0,0076 |
| 2 | 0,0278 | 0,0354 |
| 3 | 0,0716 | 0,1070 |
| 4 | 0,1304 | 0,2374 |
| 5 | 0,1789 | 0,4163 |
Следовательно, интересующая нас вероятность будет равна:
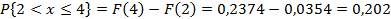
Биноминальное распределение применяется для апроксимации модели событий, возникающих:
а). При испытаниях элементов без замены. Распределение вероятностей числа вышедших из строя элементов подчиняется биномиальному распределению при условии, что условия проведения опыт постоянны;
б). При контроле качества изготовления оборудования (деталей) выборками объемом n с возвращением.
Обобщением биномиального распределения, является полиномиальное распределение.
2. Полиноминальное распределение применяется для апроксимации модели событий, когда количество исходов испытаний будет более двух (например, деталь по результатам испытаний может быть отнесена к одной из групп очень высокого, высокого, среднего качества и негодная).
В этом случае:
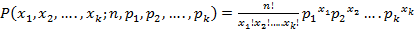 (1.15)
(1.15)
где k - количество исходов;
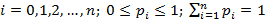
3.Распределение Пуассона.
Это распределение нашо широкое применение в технике. Оно возникает в том случае, если вероятность p появления события при каждом испытании мала, а объем испытаний велик. Часто это распределение называют распределением редких событий. Этому распределению подчиняется количество неисправностей (отказов) в заданных равных интервалах времени, число бракованных изделий в контролируемых партиях.
Распределение Пуассона имеет вид:
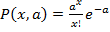 ; (1.16)
; (1.16)
где а - параметр распределения.
Распределение Пуассона является однопараметрическим. Числовые характеристики распределения (подробнее их определения приводятся в разделе 1.3):
- среднее значение
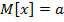 ; (1.17)
; (1.17)
- дисперсия
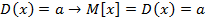 ; (1.18)
; (1.18)
- коэффициент вариации
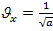 ; (1.19)
; (1.19)
- коэффициент асимметрии
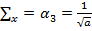 ; (1.20)
; (1.20)
- коэффициент эксцесса
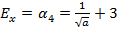 ; (1.21)
; (1.21)
При увеличении параметра a распределение Пуассона стремится к нормальному. Если а>20 , то распределение Пуассона заменяют нормальным. Распределение Пуассона часто используемся вместо биномиального распределения. Если в каждом испытании 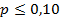 , то биномиальное распределение заменяется распределением Пуассона, т.е.
, то биномиальное распределение заменяется распределением Пуассона, т.е.
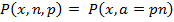 . (1.22)
. (1.22)
4. Распределение Паскаля
При испытаниях или планировании эксперимента может возникнуть задача получения заданного числа событий k на случайном отрезке времени х i .
Распределение Паскаля представляет собой распределение вероятностей длительности испытаний до получения определенного числа интересующих нас исходов, если вероятность этих исходов при каждой испытании равна р.
Распределение Паскаля является двухпараметрическим и имеет вид:
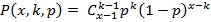 , (1.23)
, (1.23)
где х - число повторений испытаний или длительность проведения испытаний, 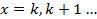 ;
;
k - количество исходов, до достижении которых испытания будут прекращены;
p - вероятность интересующего нас исходе в каждом испытании, 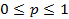 .
.
Дата: 2018-12-21, просмотров: 373.