В стальном круглом стержне
Рассчитаем теоретически скорость продольной волны в тонком стальном стержне. Для этого нам потребуются некоторые сведения из теории упругости. Закон Гука:
s = E e (6.7)
где s - механическое напряжение действующее в образце под действием некоторой внешней силы F, Н/м2, s = F / S, где S – площадь сечения образца, м2, E – модуль упругости (модуль Юнга) материала, из которого изготовлен образец, Н/м2, e - относительная деформация образца под действием внешней силы F, e = D L / L 0, где L 0 – первоначальная длина образца, D L – абсолютное удлинение ( укорочение) образца. e - величина безразмерная (м/м).
Рассмотрим стержень, в котором распространяется продольная волна в направлении от его свободного конца к закрепленному, т.е. в положительном направлении оси Х (рис.6.3). По аналогии со

Рис.6.3.Распространение продольной волны в круглом стальном стержне. Длина стержня l много больше его диаметра d (l > > d).
связанными маятниками сечения стержня в процессе распространения волны начнут вовлекаться в колебательное движение относительно
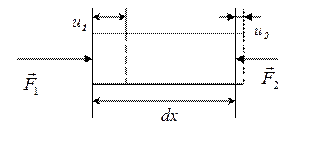
Рис. 6.4. Элементарный участок стержня в процессе распространения волны. u 1 и u 2 – смещения левого и правого сечений участка, F 1 и F 2 – силы, действующие на рассматриваемый участок со стороны соседних участков.
своего положения равновесия. Поскольку волна продольная, колебания сечений стержня будут происходить вдоль оси Х . Выделим элементарный участок стержня длиной dx (рис. 6.4).
Применим к этому участку стержня второй закон Ньютона в проекции на ось Х: 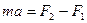 ,
, 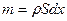 , где
, где 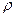 - плотность стали, S – площадь сечения стержня,
- плотность стали, S – площадь сечения стержня, 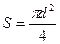 . Ускорение участка стержня – это вторая производная смещения участка по времени (частная производная, так как смещение есть функция двух переменных: времени t и координаты х):
. Ускорение участка стержня – это вторая производная смещения участка по времени (частная производная, так как смещение есть функция двух переменных: времени t и координаты х): 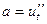 . Силы
. Силы 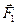 и
и 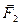 выразим через закон Гука:
выразим через закон Гука: 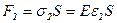 ,
, 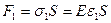 .
.
В итоге получим: 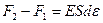 , где d e = e 2 - e 1 - дифференциал относительной деформации участка стержня (в первом приближении дифференциал равен приращению). Дифференциал функции, как известно из курса высшей математики, равен производной функции, умноженной на дифференциал аргумента:
, где d e = e 2 - e 1 - дифференциал относительной деформации участка стержня (в первом приближении дифференциал равен приращению). Дифференциал функции, как известно из курса высшей математики, равен производной функции, умноженной на дифференциал аргумента: 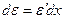 . В нашем случае относительная деформация равна
. В нашем случае относительная деформация равна 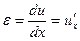 , т.к. du = u 2 - u 1 – это абсолютное удлинение участка, а dx – первоначальная длина участка. Поэтому
, т.к. du = u 2 - u 1 – это абсолютное удлинение участка, а dx – первоначальная длина участка. Поэтому 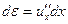 . Всё это подставим в выражение для второго закона Ньютона, получим:
. Всё это подставим в выражение для второго закона Ньютона, получим: 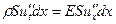 . Сокращая на площадь сечения участка и его первоначальную длину, запишем предыдущее выражение в следующем виде:
. Сокращая на площадь сечения участка и его первоначальную длину, запишем предыдущее выражение в следующем виде:
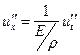 (6.8)
(6.8)
Сравним (6.8) с известным из теории волн дифференциальным уравнением плоской волны распространяющейся вдоль оси Х (уравнением Лапласа):
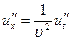 . (6.9)
. (6.9)
Получим, что скорость распространения продольной волны в тонком стержне равна: 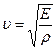 (6.10)
(6.10)
Так как модуль Юнга стали равен 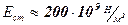 , а плотность стали
, а плотность стали 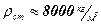 то скорость продольной волны в стержне равна
то скорость продольной волны в стержне равна 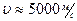 . Кстати, решением уравнения Лапласа (6.9) является уравнение плоской волны (6.2)
. Кстати, решением уравнения Лапласа (6.9) является уравнение плоской волны (6.2) 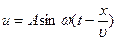 .
.
Дата: 2018-11-18, просмотров: 368.