Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотрим произвольное твердое тело, ось которого закреплена в подшипниках (рис. 4.4). Мысленно разделим это тело на n материальных точек так, что 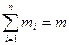. Введем дополнительные обозначения которые не нанесены на рисунке:  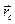- радиус – вектор центра масс (точка C);  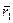- радиус– вектор точки приложения силы N ₁;  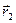- радиус–вектор точки приложения N ₂;  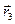- радиус–вектор точки приложения N ₃. Кроме того, из рисунка ясно что  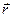- радиус – вектор точки А (точка приложения силы F), 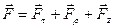, , 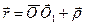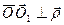. Не ограничивая общности, можно считать, что точка А совпадает с i-ой материальной точкой и соответственно точка О₁ эквивалентна точке О _i , r эквивалентно r _i , а r эквивалентно r_i

Так как мы мысленно тело разделили на n материальных точек, включая и т. А, то к получившейся системе можно применить закон изменения момента импульса (4.3а):

       

 

 

 

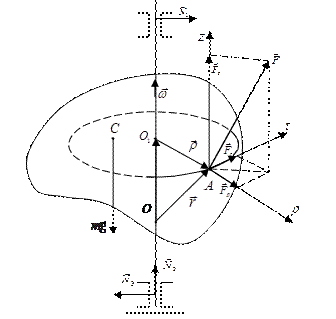
   Рис. 4.4. Вращение произвольного тела под действием силы F . F – сила приложенная к некоторой точке А тела; m – масса тела; mg – сила тяжести; N ₁, N ₃ – силы реакций подшипников; w - угловая скорость тела; N ₂ – сила реакции фланца, О₁ – центр окружности, по которой движется точка А.

                              

    

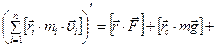
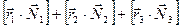                 ,                (4.4)

где в левой части – производная суммы моментов импульсов всех точек, справа – сумма моментов внешних сил. Внутренние силы, появившиеся после разделения тела на материальные точки, обеспечивают его целостность. Однако закон позволяет их не учитывать, как бы ни менялась величина и направление этих сил в процессе вращения.

       Рассмотрим левую часть уравнения (4.4). Преобразуем выражение в круглых скобках с учетом следующих соображений: 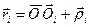, скорость i- ой точки равна 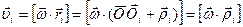, так как 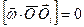. Получим: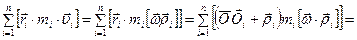 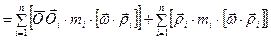       Очевидно, что первая сумма является суммой векторов, перпендикулярных оси вращения. Поэтому и сама сумма является вектором. перпендикулярным оси. Причем при более глубоком анализе можно показать, что эта сумма есть вектор, вращающийся вокруг оси с угловой скоростью w. Если тело симметрично относительно оси вращения (ось при этом проходит через центр масс тела), этот вектор равен нулю . 

     Докажем, что вторая сумма – это вектор, параллельный оси. Применим к квадратным скобкам этой суммы известную из векторной алгебры формулу “бац минус цаб”: 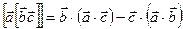 . Получим:

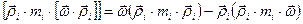. С учетом того, что вторая круглая скобка равна нулю как скалярное произведение взаимно перпендикулярных векторов 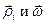, а вектор угловой скорости  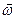одинаков для всех точек тела и лежит на оси вращения, придем к тому, что наша вторая сумма равна  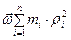и, следовательно, параллельна оси вращения. В соответствии с последним выражением удобно ввести новую для нас физическую величину – момент инерции материальной точки относительно данной оси:

                        I_i = m_iρ_i ²                             (4.5)

Соответственно, сумму моментов инерции точек можно считать моментом инерции тела:

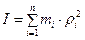                                         (4.5а)                       

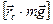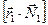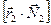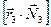 Рассмотрим правую часть уравнения (4.4). Векторные произведения , ,  и  в соответствии с правилом векторного произведения - это векторы, перпендикулярные оси вращения. Поэтому рассмотрим оставшееся векторное произведение правой части:

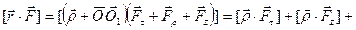
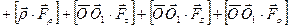Пять последних векторных произведений либо перпендикулярны оси, либо равны нулю. Параллельно оси только первое векторное произведение.

В результате если рассматривать уравнение (4.4) как сумму двух уравнений – одного, перпедикулярного оси, а другого – параллельного оси вращения, то становится ясно, что вращение тела описывается вторым:

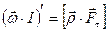                                   (4.6)                     

 так как только касательная компонента силы 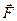, а именно  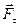заставляет тело вращаться. Поскольку момент инерции I не зависит от времени, а производная угловой скорости равна угловому ускорению, то переходя от векторов к их проекциям на ось вращения, последнее уравнение получим в виде основного уравнения динамики вращательного движения:

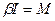                                                (4.7)              

где M – проекция момента вращающей силы на ось вращения. Уравнение, перпендикулярное оси вращения, определяет ставшие динамическими нагрузки на ось со стороны подшипников N ₁ и N ₃, вектора которых вращаются вместе с телом.

Уравнение (4.6) в отсутствие моментов сил, имеющих проекцию на ось вращения, то есть, вращающих сил или тормозящих вращение, превращается в закон сохранения проекции момента импульса на ось вращения:

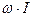                                   = const        (4.8)                          

Этот закон проявляется, в частности, когда фигурист, вращаясь, прижимает руки к груди, уменьшая тем самым свой момент инерции. При этом в соответствии с (4.8) увеличивается угловая скорость его вращения.           

 4.4. Моменты инерции различных тел. Кинетическая энергия вращающегося тела

Практически для определения момента инерции однородного тела вместо формулы (4.5а) используется определенный интеграл:

                         I = 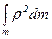                    (4.9)

где r - расстояние от элементарной массы dm до оси, относительно которой определяется момент инерции,

m - область интегрирования (вся масса тела).

Используем (4.9) для получения момента инерции тонкого стержня относительно оси перпендикулярной ему и проходящий через один из его концов (рис. 4.5). Выразим dm через длину стержня l и его массу m:

 

 

 

 

     

 

 

 Рис. 4.5. Момент инерции стержня массой m и длиной l относительно оси ОО₁  .

 

 

dm = 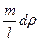. Тогда момент инерции стержня относительно оси ОО₁ будет равен определённому интегралу:

I = 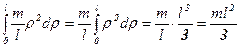                (4.10а)

Если ось проходит также, только через середину стержня, то момент инерции относительно такой оси определяется следующим образом:

I = 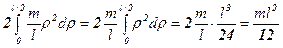    (4.10б)

Моменты инерции некоторых тел:

момент инерции цилиндра относительно его оси симметрии I = 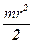 (4.10в)                        

момент инерции шара относительно любой из его осей симметрии:

                                         J = 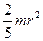                    (4.10 г)

 Теорема Штейнера: момент инерции тела относительно оси, параллельной оси симметрии равен:

                                    I ₁ = I + md ² ,                    (4.11)

 где I- момент инерции относительно оси симметрии, d- расстояние между осями, I ₁ - момент инерции относительно оси, параллельной оси симметрии.

Используя эту теорему, можно легко получить из формулы (4.10б) формулу (4.10а):     I ₁ = I + md ² = ml ² /12 + m ( l /2)² = ml ² /3 – здесь расстояние между осями равно половине длины стержня.

Определим кинетическую энергию вращающегося тела. Разобьём   тело на n материальных точек (рис. 4.6) , тогда его кинетическая энергия будет равна сумме кинетических энергий этих

точек: 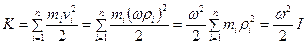  т.к из формулы (4.5а) момент инерции тела: I=  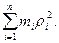В результате получим кинетическую энергию: 

                                           К = 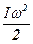                                   (4.12)

 

 

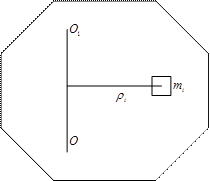
      Рис. 4.6. Вращение произвольного твердого тела вокруг оси ОО₁  .   

4.5. Применение законов динамики вращательного движения        

 Рассмотрим качение цилиндра по наклонной плоскости (рис. 4.7). Силу трения качения учитывать не будем, Тогда из 2 –го закона Ньютона:

                                        у: N – mg × cos a = 0,

                                        x: mg × sin a – F _{тр . п.}= ma.

          где F _тр.п –  сила трения покоя, действующая, так как цилиндр

движется без проскальзывания

Из основного уравнения динамики вращательного движения – формула (4.7), относительно мгновенной оси вращения , проходящей через точку О касания цилиндра, получим:                     

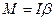 , где 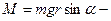 момент силы тяжести относительно данной оси, r- радиус цилиндра, 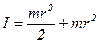- момент инерции цилиндра, определенный по теореме Штейнера, 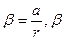- угловое ускорение цилиндра, a – ускорение центра масс цилиндра . Расписав M , I , b, получим: .          

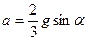Определим предельный угол наклонной плоскости 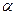, при котором начнется проскальзывание цилиндра. Это произойдет, когда величина

 

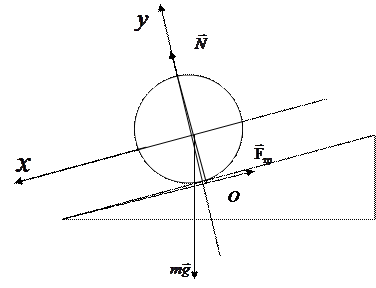
           Рис. 4.7. Качение цилиндра по наклонной плоскости.

 

трения покоя достигнет своего максимального значения – силы трения скольжения:

F _тр.п . 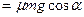. С другой стороны:

F _тр.п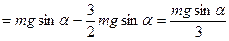

Поэтому 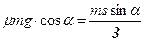 . В итоге получим условие при котором проскальзывание не наступает:

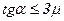
Понятие о тензоре инерции

Рассмотрим выражение в скобках в левой части уравнения (4.3а) или (4.4) - что то же самое. Это момент импульса системы материальных точек или момент импульса произвольного твердого тела, представленного такой системой точек. Будем считать, что центр декартовой системы координат совмещен с центром масс тела (рис 4.8), и в отличие от ранее рассмотренной задачи тело вращается произвольно вокруг центра масс, т.е. в разные моменты времени может вращаться вокруг разных осей вращения. При этом векторы момента импульса тела и угловой скорости могут быть неколлинеарными , т.е. не совпадать по направлению, даже в отсутствие внешних сил.

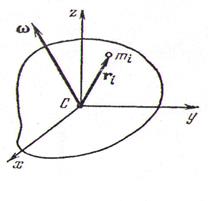
          Рис 4.8. Произвольное вращение твердого тела.

 

Распишем момент импульса тела: 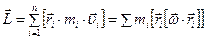 - здесь мы скорость каждой материальной точки (элементарной массы) заменили векторным произведением угловой скорости тела на радиус-вектор точки – формула (3.2) и вынесли массу как скалярную величину за знак векторного произведения. Теперь воспользуемся формулой «бац минус цаб»: 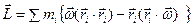.  Напомним, что суммирование осуществляется по всем элементар­ный массам, на которые мысленно разбито тело. Скалярные произведения векторов в скобках выразим через сумму произведений их проекций на оси:  ,

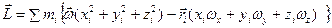где x_i , y_i , z_i – проекции радиус-вектора точки на оси координат (в данном случае координаты точки), w _x , w _y , w _z – проекции вектора угловой скорости тела.

Найдем проекцию этого вектора на ось х: =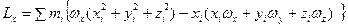

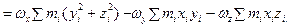
Аналогично находятся проекции вектора L на оси у и z :

 

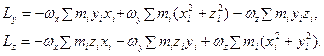
Теперь удобно записать связь момента импульса тела с его угловой скоростью в матричной форме:

                     L = Iw                           (4.13)

где L = 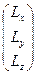 - вектор момента импульса, w =  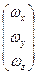- вектор угловой скорости, I =  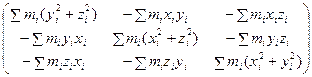- тензор инерции.

Тензор инерции – это квадратная матрица третьего порядка, и

перемножив тензор инерции и вектор угловой скорости по правилу

перемножения матриц, мы можем еще раз убедиться в правильности

формулы (4.13). Диагональные компоненты тензора представляют собой в соответствии с формулой (4.5) моменты инерции нашего тела относительно осей X , Y и Z . Эти компоненты называются осе­выми моментами инерции. Недиагональные компо­ненты называются центробежными моментами инерции. Заметим, что недиагональные компоненты тензора удовлетворяют условию; 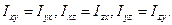 Тензор, удовлетворяющий такому условию, называется симмет­ричным. Записав тензор инерции с помощью компонент, получим более компактную форму:

                  I =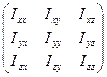                             

Надлежащим образом повернув декартову систему координат вокруг ее начала, т.е. вокруг центра масс тела, можно добиться того, чтобы все недиагональные компоненты тензора инерции стали равны нулю. В этом случае координатные оси совпадут с так называемыми главными осями инерции тела. При этом проекции того же вектора момента импульса будут выражены через проекции того же вектора угловой скорости следующим образом: 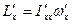 ,  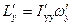,  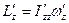 . Все проекции и диагональные компоненты тензора инерции определены уже в новой системе координат.

Таким образом, у любого твердого тела есть три взаимно перпендикулярные оси, пересекающиеся в центре инерции, который у однородного тела любой формы совпадает с центром масс. Эти оси называются главными осями инерции. Моменты инерции тела относительно главных осей называются главными моментами инерции. В нашем случае 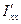 ,  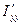,  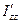- главные моменты инерции. Если тело вращается вокруг любой из своих главных осей инерции, то, как следует из (4.13), его вектора момента импульса и угловой скорости коллинеарны, т.е. совпадают по направлению. При этом, если на тело не действуют моменты внешних сил, такая ось вращения, будучи незакрепленной, остается неподвижной во время вращения.

Гироскоп

Гироскопом называется симметричное массивное тело, вращающееся вокруг оси симметрии, совпадающей с одной из главных осей инерции. Угловая скорость вращения w достаточно велика. Как было сказано в предыдущем параграфе, в отсутствие моментов внешних сил эта ось вращения будет оставаться неподвижной, а вектора момента импульса L и угловой скорости w  будут совпадать по направлению.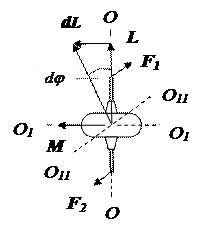  

 

Рис. 4.9. Поворот оси гироскопа под действием внешних сил F ₁ и F ₂.

Приложим к оси гироскопа ОО пару сил F ₁ и F ₂, параллельных оси О₁₁О₁₁ (рис. 4.9). Эта ось перпендикулярна плоскости рисунка.

Казалось бы, ось гироскопа должна повернуться вокруг оси О₁О₁ , однако она поворачивается вокруг оси О₁₁О₁₁  за время dt на угол d j . Это происходит в согласии с законом изменения момента импульса (4.3) или (4.3а). В нашем случае его удобно записать с помощью дифференциалов: dL=Mdt (1) , где dL – изменение (дифференциал) вектора момента импульса, M – момент пары сил F ₁ и F ₂ – на рисунке вектор момента сил лежит на оси О₁О₁. Радиус-векторы этих сил выходят из центра гироскопа - на рисунке они не показаны. Момент пары сил определяется как сумма моментов каждой силы или как удвоенный момент любой из них, так как и радиус-векторы, и силы равны по модулю.

При малых углах d j , как видно из рисунка, dL / L = tgd j » d j. С другой стороны, по определению (3.1): d j / dt = w ₁ , где w ₁ – модуль угловой скорости поворота вектора L . Таким образом, с учетом равенства (1) получим: w ₁=M / L (2). Обычно w ₁<<w , поэтому ось гироскопа в таких случаях в любой момент времени совпадает с вектором момента импульса гироскопа. Таким образом, в результате действия пары сил гироскоп действительно повернется вокруг оси О₁₁О₁₁. Вектора w ₁  , M , L связаны аналогичным равенству (2) векторным соотношением: M =[w ₁ L]    (4.14)                                   

Соответственно, модуль вектора M в общем случае равен:   

                                    M = w ₁ Lsin a                                 (4.15)

где a - угол между векторами w ₁ и L  (в нашем случае он равен  90 градусам).

Рассмотрим гироскоп в поле силы тяжести. Ось гироскопа шарнирно закреплена в точке О (рис. 4.10). Модуль вектора момента силы тяжести, приложенного к гироскопу, равен:

                                       M = mglsin a                (4.16)                                     

где m – масса гироскопа, l – расстояние от точки О до центра масс

гироскопа, 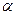- угол, образованный осью гироскопа с вертикалью. Направлен вектор M перпендикулярно вертикальной плоскости, проходящей через ось гироскопа (на рисунке эта плоскость заштрихована). За время dt вектор момента импульса гироскопа получит приращение: dL=Mdt . Соответственно этому приращению переместится ось гироскопа . Вектор dL таким образом в любой момент времени будет перпендикулярен каждому предыдущему положению оси гироскопа. Ось гироскопа будет поворачиваться вокруг вертикали,

   

 

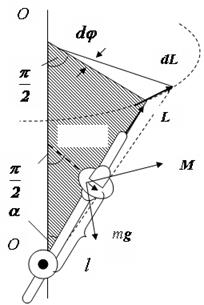
Рис. 4.10. Прецессия гироскопа в поле силы тяжести.

 

описывая конус с углом при вершине, равным 2 a. Такое движение гироскопа называется прецессией. Угловую скорость прецессии w ₁ можно найти из (4.15) и (4.16): w ₁=mgl / L .