Глава 5. Колебания

5.1. Гармонические колебания без трения

Гармоническим колебанием материальной точки является такое ее движение, при котором смещение точки от положения равновесия зависит от времени по закону синуса или косинуса. Рассмотрим шарик массой m, висящий на пружине жесткостью к (рис. 5.1).

Рис. 5.1. Шарик, висящий на пружине – начало оси Х совпадает с положением равновесия шарика.  

Сместим шарик вниз на расстояние 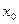 и отпустим его, одновременно включив секундомер. Применим к шарику второй закон Ньютона в проекции на ось Х: 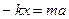, где kx – сила упругости, х – в нашем случае координата шарика. Мы не учитываем равные по величине и противоположные по знаку проекции силы тяжести и части силы упругости. Так как 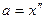, то последнее уравнение можно записать в виде: 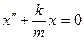. Обозначив:  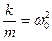                (5.1) 

получим стандартное дифференциальное уравнение колебаний точки:

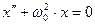                                               (5.2)

Решением этого дифференциального уравнения является функция:

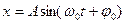                                            (5.3)

которая определяет координату шарика х в любой момент времени t . В формуле (5.3):       А – амплитуда колебаний шарика, м

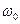         - циклическая частота, рад/с

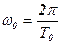           , Т₀ – период колебаний, с

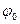         - начальная фаза, рад

Взяв первую и вторую производные, получим соответственно выражения для скорости и ускорения:

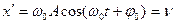(5.3а)  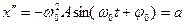                        (5.3б)

Определим A и 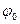 для нашего конкретного случая из начальных условий колебаний: при t=0 координата шарика x=x₀, начальная скорость 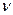=0. Подставив эти величины в (5.3) и (5.3а), получим систему уравнений:

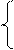
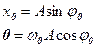
Решая вначале второе уравнение, получим 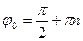, n=0,±1,... Подставив выражение для начальной фазы в первое уравнение, придем к значениям амплитуды и начальной фазы: 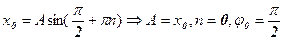. Таким образом, зависимость координаты нашего шарика от времени имеет следующий вид: 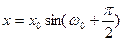. В данном случае амплитуда равна начальному смещению шарика от положения равновесия. Графики смещения (координаты) и скорости шарика от времени приведены на рисунках (5.2) и (5.3).

 Рис. 5.2. График зависимости смещения колеблющейся точки от времени.

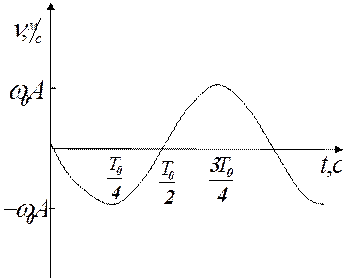
Рис. 5.3. График зависимости скорости колеблющейся точки от времени.

Физический маятник

Физическим маятником называется произвольное твердое тело, закрепленное на оси, не проходящей через центр масс, и способное совершать колебания относительно положения равновесия (рис 5.4). В положении равновесия отрезок СО лежит на вертикали. Если отклонить физический маятник на угол j, то появится момент силы тяжести и после отпускания маятника, он начнет совершать колебания. Определим период этих колебаний, считая угол j достаточно малым. Момент силы тяжести равен: М=- mglsin j , знак минус вызван тем, что момент силы и угол поворота  в нашем случае имеют противоположные знаки.

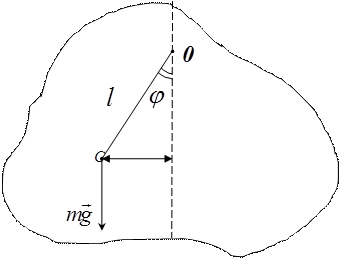
        Рис 5.4. Колебания физического маятника. С- центр масс; m- масса тела; О – точка, через которую проходит горизонтальная ось; 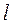- расстояние между центром масс и осью крепления.

Из основного уравнения динамики вращательного движения: M = I b , где I – момент инерции физического маятника относительно оси крепления, b - угловое ускорение маятника, равное второй производной угла поворота: 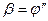, и с учетом того, что при малых углах sin j = j, получим: 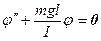. Обозначив 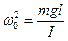, придем к стандартному дифференциальному уравнению 

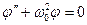          (5.4), аналогичному (5.2). Это означает, что при отсутствии сил трения и сопротивления физический маятник будет совершать такие же гармонические колебания, как и шарик на пружине, с циклической частотой w ₀ и соответственно с периодом:

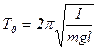                                                        (5.5)

Из формулы (5.5) можно получить формулу для периода математического маятника. Математический маятник – материальная точка на невесомой нити длиной 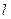. Момент инерции материальной точки (4.5): 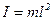. Подставив его в (5.5), получим формулу для периода колебаний математического маятника:

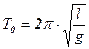                                                                   (5.5а)