Момент импульса, момент силы

Моментом импульса материальной точки относительно точки 0 называют (рис. 4.1) вектор:

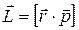                       (4.1)                 

где L – момент импульса 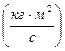; r - радиус-вектор

  Рис. 4.1. Радиус-вектор 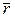и импульс  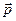материальной точки. 

материальной точки ( соединяет точку 0 и положение материальной точки в данный момент времени), 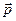 - импульс материальной точки, .

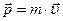Моментом силы F относительно точки 0 называется вектор:

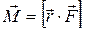
                                  (4.2)                   

Заметим, что момент силы не зависит от точки приложения силы ( силу можно перемещать вдоль её линии действия). Действительно, определим моменты одной и той же силы F , приложенной в двух точках O ₃ и O ₁ , расположенных на линии действия силы F (рис. 4.2). По определению момента силы:

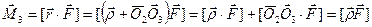 , поскольку векторное произведение параллельных векторов O ₂ O ₃ и F  равно 0. Аналогично:  .

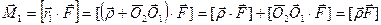 Необходимо отметить, что модуль вектора момента силы равен: 

                           M  = r × F ,        где 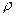 - перпендикуляр к линии действия силы (рис. 4.2), называемый плечом силы F .

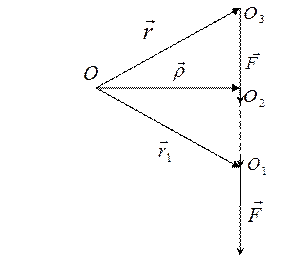
Рис. 4.2. Моменты силы F , приложенной в точках O ₁ и O ₃ .

Закон изменения момента импульса системы материальных точек

Рассмотрим две взаимодействующие между собой материальные точки массой m ₁ и m ₂ (рис. 4.3). Запишем второй закон Ньютона для двух материальных точек:

          .

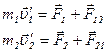Умножим первое уравнение векторно слева на 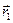, а второе уравнение таким же образом на 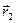. Получим: 

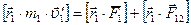
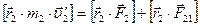                 (1)

Рис. 4.3. Система двух материальных точек. 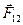,  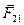- внутренние силы; 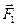,  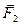- равнодействующие внешних сил, приложенных к точкам m ₁ и m ₂ ; 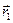,  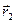- радиус-векторы этих точек.

Докажем, что 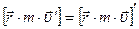. То есть докажем, что в данном случае знак производной можно вынести за квадратные скобки векторного произведения: 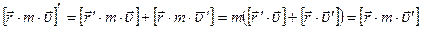Здесь использована формула производной произведения двух функций, а также то, что скалярную величину (в данном случае массу) можно вносить и выносить за знак векторного произведения и что производная радиус-вектора материальной точки – это скорость, а векторное произведение вектора на самого себя равно нулю.

 Сложим уравнения системы (1) с учетом доказанного тождества и с учетом того, что сумма производных равна производной суммы. Получим закон изменения момента импульса системы двух материальных точек:

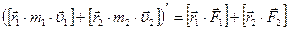(4.3)                 

так как по 3-му закону Ньютона 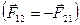 и следовательно, два слагаемых в правой части дают в итоге: 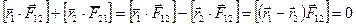, поскольку векторное произведение двух параллельных векторов равно нулю.

      Запишем (4.3) словами: производная суммы моментов импульсов двух материальных точек равна сумме моментов внешних сил, действующих на эти материальные точки. Аналогично можно доказать закон изменения момента импульса для системы n материальных точек:   

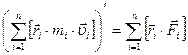                             (4.3а).