Свяжем линейную скорость произвольной точки тела с его угловой скоростью. Докажем справедливость следующей формулы для

линейной скорости точки А (рис. 2.2):

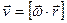                                                   (2.2)

Определим вначале выражение для модуля ν. По определению скорости - формула (1.1): 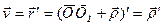 (см. рис.2.2). Таким образом в нашем случае скорость равна производной вектора r . Поэтому модуль скорости 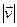= = 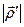= 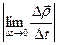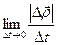. Определим

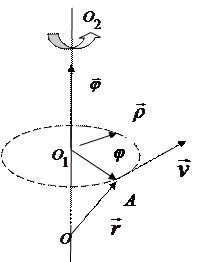
            Рис. 2.2. Векторные величины, характеризующие вращение тела: 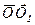-вектор, лежащий на оси вращения О₂О₂ , 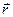- радиус- вектор точки А , 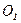-центр окружности, по которой движется произвольная точка А данного тела, φ- вектор угла поворота (углового пути), вектор угловой скорости ω направлен так же, как и вектор φ, ν- вектор линейной скорости точки А , r - вектор, соединяющий центр окружности с точкой А , φ – модуль вектора φ.

модуль вектора D r:  Из рисунка (2.3) видно, что 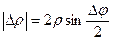 как основание равнобедренного треугольника. Поэтому модуль вектора скорости будет равен:

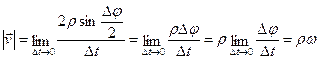
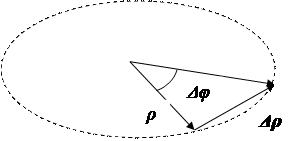
    Рис. 2.3. Определение модуля вектора D r:

Мы воспользовались тем фактом, что пр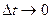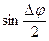и ,   и 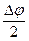 являются эквивалентными бесконечно малыми величинами и одну можно заменить другой. Кроме того, мы использовали свойства предела - постоянную можно вынести за знак предела. И, наконец, мы воспользовались тем, что в случае вращения вокруг неподвижной оси

модуль угловой скорости равен производной модуля угла поворота: 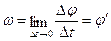. Таким образом, модуль скорости равен:

                                           ν=ρω                     (2.3)

 Докажем, что модуль скорости, определяемой по формуле (3.2), также равен ν=ρω. Для этого: 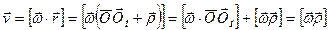- первая квадратная скобка как векторное произведение параллельных векторов равна нулю. Модуль последнего выражения равен 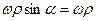, т.к .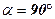

 Установим направление вектора скорости, определяемой по формуле (2.2). Так как ранее мы получили, что 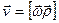, а из рисунка (2.2) видно, что вектор ν перпендикулярен плоскости, образованной векторами w и r и направление действительно определяется правилом правого винта. Формула (2.2)доказана полностью.

Применим формулу (2.2), чтобы получить выражение для ускорения точки А :

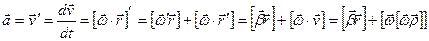Так как производная произведения равна известному соотношению, производная угловой скорости равна угловому ускорению, производная радиус-вектора точки равна скорости, а векторное произведение трех векторов может быть выражено через скалярные произведения этих векторов по формуле “бац минус цаб”: 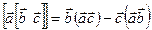, поэтому .

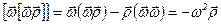 Таким образом, ускорение точки, как и следовало ожидать в соответствии с формулой (1.4) из первой главы, равно сумме двух векторов - тангенциального и нормального ускорений:

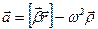                                                 (2.4)    

Глава 3. Динамика поступательного движения. Законы сохранения