Первый закон Ньютона: существуют такие системы отсчета, в которых если на тело не действуют другие тела или их действие скомпенсировано, то тело покоится или движется равномерно прямолинейно, Такие системы отсчета называются инерциальными.

Инерциальной является система отсчета, связанная с центром масс Солнечной системы (приблизительно центр Солнца). Система отсчета, движущаяся равномерно прямолинейно относительно инерциальной, также является инерциальной. Приблизительно инерциальной является система отсчета связанная с центром Земли (ускорение центра Земли относительно центра Солнца очень мало: 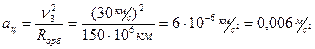.)  Система отсчета связанная с какой-либо точкой поверхности Земли не всегда, даже приблизительно, может считаться инерциальной.

 Второй закон Ньютона: произведение массы тела на его ускорение равно векторной сумме всех сил, действующих на тело:

m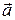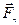^. = + +…+                                          (3.1)

Третий закон Ньютона: если два тела взаимодействуют между собой, то их силы взаимодействия равны по величине и направлены противоположно друг другу:

                                                        (3.2)

где 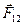-сила действующая на первое тело со стороны второго; 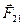- сила действующая на второе тело со стороны первого.

Закон изменения импульса

Импульсом тела (материальной точки) называется вектор:

                                                     (3.3)                    

где m – масса тела, v – его скорость. Рассмотрим два взаимодействующих между собой тела (материальные точки) (рис 3.1). 

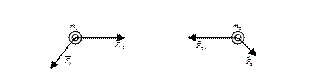
Рис 3.1. Взаимодействие двух тел массой m ₁  и m ₂.  - векторная сумма всех сил, действующих на первое тело со стороны третьих (внешних) тел; 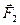 - векторная сумма всех сил, действующих на второе тело со стороны третьих (внешних) тел; 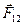-сила действующая на первое тело со стороны второго; 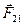- сила действующая на второе тело со стороны первого.

Cилы  и 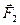  называются равнодействующими внешних сил, а 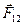,  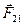- внутренними силами. Применим к телам m ₁  и m ₂  второй закон Ньютона:

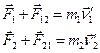
 Сложим уравнения, внеся массы, являющиеся при нерелятивистских скоростях константами, под знак производных и учтя, что по третьему закону Ньютона 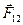+ 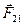=0. Получим: . Так как сумма производных равна производной суммы, то из последнего выражения получим закон изменения импульса системы двух тел:

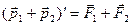                                         (3.4)                                    

        В отсутствие внешних сил 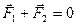, и из формулы (3.4) вследствие равенства нулю производной получим закон сохранения импульса в изолированной системе двух тел:

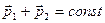                                           (3.5)                                        

Аналогично формуле (3.4) можно получить закон изменения импульса системы n материальных точек (тел):

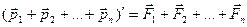              (3.4а)                       

В отсутствие внешних сил соответственно будет справедлив закон сохранения импульса в изолированной системе n тел . Из него, в частности следует, что сумма импульсов Солнца, планет, астероидов и других тел Солнечной системы остается постоянной.