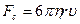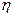Вернемся к шарику на пружине, но усложним задачу, поместив шарик в вязкую жидкость (рис. 5.5). Со стороны жидкости на шарик действует сила сопротивления Стокса: , где -коэффициент вязкости жидкости, 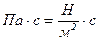, r – радиус шарика, м, 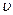- скорость шарика, м/с.

      Запишем второй закон Ньютона для шарика в проекции на ось Х, не учитывая равнодействующую (векторную сумму) сил тяжести и Архимеда и уравновешивающую ее часть силы упругости: 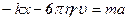, где kx – оставшаяся часть силы упругости. Проекции сил Стокса и упругости взяты с минусом, так как проекция скорости шарика u и его координата х всегда противоположны им по знаку. Скорость и ускорение шарика равны соответственно первой и второй производной координаты, т.е. 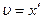, 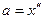. Введем обозначения: 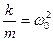, 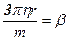. Получим стандартное уравнение колебаний с трением:

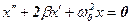                                      (5.6)

            Рис. 5.5. Колебания шарика в вязкой жидкости, положение равновесия совпадает с нулем оси Х.

Решением данного однородного дифференциального уравнения 2-го порядка является следующая функция координаты шарика от времени:

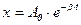
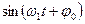                            (5.7)

где 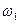 -циклическая частота данных колебаний с трением:

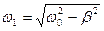          ,                     (5.8)

   А₀ – начальная амплитуда шарика, м.

График этой функции приведен на рис. 5.6, из него видно, что амплитуда колебаний со временем уменьшается. Такие колебания называются затухающими. Величина b характеризует это затухание. При достаточно больших ее значениях ( w ₀ < b ) w ₁ в соответствии с формулой (5.8) становится комплексным числом. Физический смысл этого заключается в следующем: после смещения шарика от положения равновесия и отпускания он медленно возвращается в положение равновесия, и затухающие колебания при этом не возникают. 

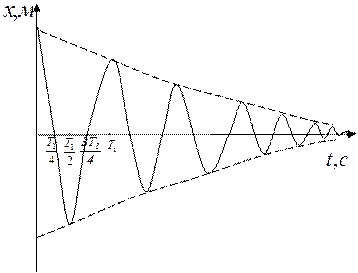
            Рис. 5.6. График затухающих колебаний – показан сплошной линией, прерывистые линии – графики А= ± А₀е^{- b t}, период колебаний Т₁ = 2 p / w ₁ .

5.4. Вынужденные колебания в системе с трением

Рассмотрим еще более сложную модель колебательной системы (рис. 5.7). Прикрепленный к потолку резервуар с вязкой жидкостью снабжен внизу дополнительным отверстием с уплотнением, по которому может перемещаться невесомый шток, соединенный с шариком. К штоку приложена периодическая сила 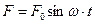, где F ₀ – амплитуда этой силы, Н, w - циклическая частота, рад/с. Запишем для шарика второй закон Ньютона в проекции на ось Х: 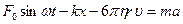. Введем обозначения  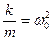, , 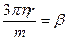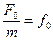. Получим стандартное уравнение вынужденных

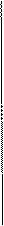
         Рис. 5.7. Вынужденные колебания шарика в системе с трением.

колебаний с вязким трением:

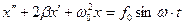                                       (5.9)

 Оно отличается от уравнения (6.6) наличием правой части и называется поэтому неоднородным дифференциальным уравнением второго порядка. Общим решением его является сумма общего решения однородного уравнения (5.6) и любого частного решения неоднородного уравнения (5.9). Общее решение однородного уравнения – это быстро убывающая со временем функция (5.7), и ее вкладом в движение шарика спустя некоторое время можно пренебречь. Частное же решение данного неоднородного уравнения, как следует из математики, должно иметь такой же вид, как и его правая часть. Поэтому будем искать частное решение в виде:

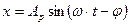                                       (5.10)

        где А_р- искомая амплитуда колебаний шарика, м, 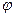 - искомая начальная фаза, рад, 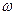- в нашем случае частота колебаний внешней силы, рад/с.

            Подставим предполагаемое решение в исходное уравнение (5.9), для этого вычислим первую и вторую производную координаты шарика х, т.е. скорость и ускорение:

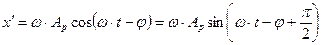
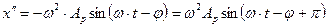 - здесь использованы известные из тригонометрии формулы приведения. Тогда получим:

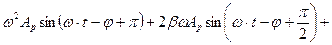
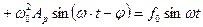                                    (5.11)

Правая часть этого уравнения является по сути суммой проекций на вертикальную ось трех вращающихся с циклической частотой w векторов, выходящих из одной точки и повернутых относительно друг друга на углы p и p /2 . В правой части – проекция на ту же ось четвертого вращающегося вектора, выходящего из той же точки и повернутого по часовой стрелке относительно одного из трех других на угол j . Все четыре вектора изобразим в виде диаграммы в тот момент времени, когда вектор, модуль которого равен w ₀ ² А_р , совпадает с осью Х (рис. 5.8).

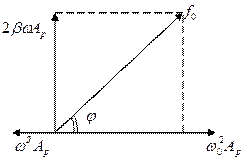
       Рис. 5.8. Векторная диаграмма, соответствующая уравнению (5.11).

Очевидно, что сумма самих трех векторов равна четвертому, коль то же самое справедливо для их проекций в любой момент времени. Поэтому из диаграммы с учетом правил сложения векторов и теоремы Пифагора следует:

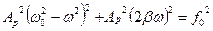
Из последнего равенства легко найти результирующую амплитуду :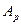                             

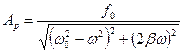                           (5.12)

А из самой диаграммы также нетрудно определить угол j :

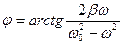                                           (5.13)

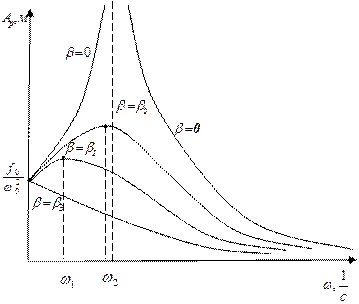
Рис. 5.9. Графики зависимости амплитуды колебаний шарика от циклической частоты внешней силы для различных коэффициентов затухания: b ₃>b ₂>b ₁ .

Исследуем подкоренное выражение (5.12) на экстремум, считая аргументом w. Для этого возьмем производную по w и приравняем ее к 0: 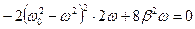. Получим: 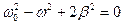, и, наконец, найдем значения циклической частоты внешней силы, при которых результирующая амплитуда колебаний шарика достигает максимума:

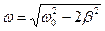                                                            (5.14)

С учетом этого построим графики функций 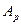 от 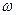 для различных коэффициентов затухания b (рис. 5.9). Амплитуда колебаний шарика достигает максимума (резонанса) при различной циклической частоте внешней силы – чем меньше коэффициент затухания, тем больше эта частота и больше амплитуда колебаний шарика при резонансе. В идеальном случае, когда трения нет, т.е. b =0, резонанс достигается при частоте внешней силы, равной w ₀ , а амплитуда колебаний при этом стремится к бесконечности. Если коэффициент затухания достаточно велик, под корнем в формуле (5.14) появляется 0 или даже отрицательное число. Это означает, что резонанса не возникает и чем больше частота внешней силы, тем меньше амплитуда колебаний шарика – график, соответствующий b ₃ .

Глава 6. Волны