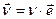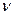Для того чтобы взять производную, необходимо записать вектор скорости следующим образом: , где - модуль вектора

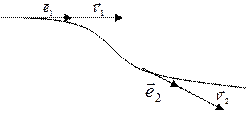
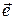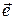Рис. 1.2. Единичные векторы ₁ и ₂  .

скорости; 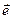- единичный вектор, совпадающий в каждой точке траектории с вектором скорости (рис.1.2).

Тогда производная определяется по правилу производной произведения:

Рис. 1.3. Определение разности векторов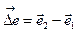  

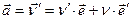                                                 (1.3а)                                         

где 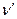 - производная модуля скорости; 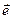- единичный вектор;  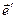- производная единичного вектора .

По определению производной:

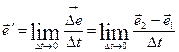. Модуль вектора  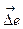(рис. 1.3) равен основанию равнобедренного треугольника с боковыми сторонами, равными единице. При малых углах  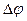между векторам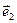и  и 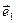 синус угла примерно равен самому углу, выраженному в радианах. Поэтому модуль производной единичного вектора можно выразить следующим образом:

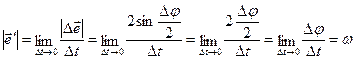 Последний предел по определению равен модулю угловой скорости поворота  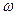единичного вектора .

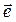Определим направление производной единичного вектора 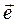. Как видно из рисунка 1.3 направление вектора  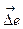при 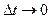 стремится к перпендикуляру к траектории в этой точке, поэтому производная единичного вектора 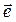может быть записана следующим образом:

        ,

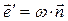 где 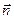- единичный вектор, в любой точке траектории перпендикулярный вектору .

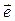В результате получим формулу для ускорения материальной точки:

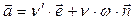                                (1.3б)                             

Из нее следует, что вектор ускорения в любой точке траектории является суммой двух взаимно перпендикулярных векторов (рис 1.4), тангенциального а _t и нормального а _n ускорений.

Рис.1.4. Нормальное а _n , тангенциальное а _t  и полное а ускорения в произвольной точке траектории.

 Из рис.1.4 и формулы (1.3б) понятно, что модуль полного ускорения равен

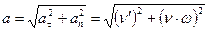         (1.4)                                                                                                           

Глава 2.Кинематика вращательного движения  

    2.1. Векторы угла поворота, угловой скорости и ускорения

Приведем некоторые сведения из векторной алгебры, которые потребуются в дальнейшем. Векторным произведением двух векторов a и b называется вектор c , получаемый с помощью определителя 3-го порядка в том случае, когда известны проекции векторов на оси координат:

  =

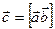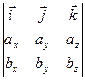
где вектора i, j, k –единичные вектора выходящие из начала координат и лежащие соответственно на осях x, y, z. Иначе векторное произведение определяется следующим образом ( рис. 2.1): вектор c перпендикулярен плоскости, образованной векторами a и b , модуль вектора с  равен произведению модулей векторов a и b на синус угла между ними: с = а bsinα; направление вектора с определяется правилом правого винта : вращая винт от первого вектора ко второму (в нашем случае от а к b), определяем направление поступательного движения винта, и это направление совпадает с направлением вектора с .

Рассмотрим вращающееся вокруг неподвижной оси произвольное твердое тело (рис. 2.2). Углом поворота тела называется вектор φ , модуль которого численно равен углу поворота вектора ρ любой точки вращающегося тела (в нашем случае точки А), выраженному в радианах, а направление определяется правилом правого винта. В соответствии с этим правилом данный вектор лежит на оси вращения и направлен вверх (см. рис.2.2).

Вектором угловой скорости вращающегося тела называют производную вектора угла поворота по времени:

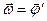
                                                   (2.1)             

 размерность [w]=рад/с.  Если тело вращается вокруг неподвижной оси, вектора φ и ω лежат на оси вращения.

Вектором углового ускорения вращающегося тела называют производную вектора угловой скорости по времени:

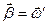                                                         (2.1а)

размерность [b]= рад/с²

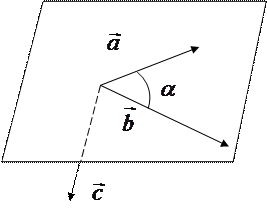Рис. 2.1. Вектор с , являющийся результатом векторного произведения вектора а на вектор b , ^ , ^ .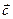   

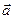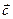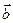Если угловая скорость возрастает, вектор углового ускорения совпадает по направлению с вектором ω , если уменьшается, вектор углового ускорения направлен противоположно ему. Понятно, что для всех точек вращающегося тела все эти три вектора одинаковы, поэтому можно говорить о векторах угла поворота (или углового пути), угловой скорости и углового ускорения вращающегося тела.