Механические колебания и волны

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Содержание

Введение……………………………………………………………….....5

Механика твердого тела

Глава 1. Кинематика поступательного движения……………………..7

1.1. Скорость и перемещение точки………………………………..7

1.2. Нормальное и тангенциальное ускорения…………………….8

Глава 2. Кинематика вращательного движения……………………..10

2.1. Векторы угла поворота, угловой скорости и ускорения…….10

2.2. Связь линейных и угловых величин ……………………….....12

Глава 3. Динамика поступательного движения.

Законы сохранения……………………………………………...14

3.1. Инерциальные системы. Законы Ньютона…………………....14

3.2. Закон изменения импульса………………………………….....15

3.3. Центр масс произвольного тела……………………………….16

3.4. Работа переменной силы. Кинетическая энергия……………..18

3.5. Потенциальные силы, потенциальная энергия.

Закон охранения механической энергии ……………………..20

3.6. Неинерциальные системы отсчета……………………………...22

Глава 4. Динамика вращательного движения…………………………..24

4.1. Момент импульса, момент силы………………………………...24

4.2. Закон изменения момента импульса системы

материальных точек……………………………………………..26

4.3. Вращение произвольного твердого тела

вокруг закрепленной оси………………………………………..27

4.4. Моменты инерции различных тел. Кинетическая

энергия вращающегося тела………………………………….....31

4.5. Применение законов динамики вращательного движения….....33

4.6. Понятие о тензоре инерции………………………………………34

4.7. Гироскоп…………………………………………………………...37

Механические колебания и волны

Глава 5. Колебания………………………………………………………...40

5.1. Гармонические колебания без трения……………………………40

5.2. Физический маятник………………………………………………43

5.3. Колебания в системе с трением………………………………….44

5.4. Вынужденные колебания в системе с трением………………….46

Глава 6. Волны……………………………………………………………..50

6.1. Колебания связанных маятников………………………………...50

6.2. Продольные и поперечные волны. Фронт

волны. Длина волны. Интерференция волн……………………51.

6.3. Скорость распространения продольной волны в стержне……..53

6.4. Энергия волны. Плотность энергии……………………………..56

Вопросы для самостоятельной работы…………………………………..58

Литература………………………………………………………………64

Словарь терминов……………………………………………………….65

Введение

В разделе “Механика твердого тела” очень важным является понимание взаимосвязи между векторными физическими величинами в основных законах и определениях. Например, сила – это вектор, направление и длина которого показывают, как одно тело действует на другое. Также нетрудно интерпретировать направление и длину таких векторов, как перемещение материальной точки и ее радиус-вектор. Вектор же скорости материальной точки имеет свойство – быть касательным к траектории точки, вытекающее из определения скорости как производной радиус-вектора. Более сложным для понимания является вектор ускорения, являющийся производной вектора скорости материальной точки. Его приходится представлять в виде суммы взаимно перпендикулярных векторов – тангенциального и нормального ускорений. Первое “отвечает” за изменение длины (модуля), а второе – за изменение направления вектора скорости. При этом в одних случаях, например, когда тело брошено вертикально вверх или вниз, или когда автомобиль, двигаясь прямолинейно, тормозит или ускоряется, длина и направление вектора ускорения имеют вполне понятный смысл. В других случаях, например, когда материальная точка движется неравномерно по окружности, направление и длина вектора ускорения мало что дают для анализа движения. Здесь необходимо вектор ускорения рассматривать как сумму нормального и тангенциального ускорений.

Еще более сложным является применение таких “неочевидных” векторов, как момент импульса материальной точки или твердого тела и момент силы. Они используются по сути как специальный математический аппарат для того, чтобы из законов Ньютона получить законы динамики вращательного движения в самой общей форме, а потом, применив их в конкретной ситуации, получить более удобные скалярные соотношения, как это будет сделано в главе 4. И только, пожалуй, в параграфе о гироскопах длина и направление вектора момента силы и параллельного ему вектора приращения момента импульса приобретают наглядный смысл, указывая направление поворота оси гироскопа. Однако эта ситуация исключительная, связанная со спецификой гироскопа, как такового.

В главе 5 “Механические колебания и волны”, как и в предыдущих главах, применяется второй закон Ньютона. Решая полученные дифференциальные уравнения, получают закон изменения координаты шарика при его свободных гармонических колебаниях на

пружине. Далее применяются законы динамики вращательного движения из главы 4 и в результате получают математически тот же закон, но уже в отношении угла отклонения физического маятника от положения равновесия. На следующем этапе продолжается применение второго закона Ньютона для систем, совершающих затухающие колебания и вынужденные колебания с трением. Необходимо заметить, что получаемые при этом дифференциальные уравнения имеют стандартный вид и изучаются в курсе высшей математики практически одновременно. Для решения последнего из них в нашем курсе используется метод векторных диаграмм, который будет применяться и в следующих разделах физики, в частности электромагнетизме и оптике. Полученное решение позволяет построить резонансные кривые, которые широко применяются, в частности, для изучения механических систем с внешней периодической силой, например подвески колеса автомобиля.

В главе 6 “Механические волны” осуществлен переход от колебаний к волнам в модели связанных маятников. Эта модель по математическому описанию совпадает с моделью плоской волны и с ее помощью легко получается так называемое уравнение плоской волны. Для вывода дифференциального уравнения Лапласа, решением которого и является уравнение плоской волны, применяется второй закон Ньютона и закон Гука для малого участка упругого стержня, по которому распространяется продольная волна. Здесь надо отметить, что оба закона применяются к деформируемому телу, так как здесь неприменима ранее используемая модель твердого тела. Далее приводится вывод формулы потенциальной энергии деформации участка стержня. В нем использована аналогия деформированного стержня с пружиной. Здесь, как в случае с физическим маятником и шариком на пружине, различные объекты описываются одинаковыми по структуре формулами.

Механика твердого тела

Закон изменения импульса

Импульсом тела (материальной точки) называется вектор:

(3.3)

где m – масса тела, v – его скорость. Рассмотрим два взаимодействующих между собой тела (материальные точки) (рис 3.1).

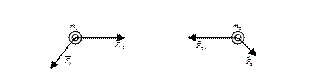
Рис 3.1. Взаимодействие двух тел массой m ₁ и m ₂. - векторная сумма всех сил, действующих на первое тело со стороны третьих (внешних) тел; 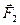- векторная сумма всех сил, действующих на второе тело со стороны третьих (внешних) тел; 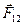-сила действующая на первое тело со стороны второго; 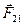- сила действующая на второе тело со стороны первого.

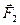Cилы и называются равнодействующими внешних сил, а 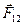, 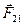- внутренними силами. Применим к телам m ₁ и m ₂ второй закон Ньютона:

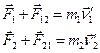
Сложим уравнения, внеся массы, являющиеся при нерелятивистских скоростях константами, под знак производных и учтя, что по третьему закону Ньютона 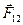+ 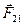=0. Получим: . Так как сумма производных равна производной суммы, то из последнего выражения получим закон изменения импульса системы двух тел:

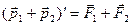(3.4)

В отсутствие внешних сил 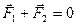, и из формулы (3.4) вследствие равенства нулю производной получим закон сохранения импульса в изолированной системе двух тел:

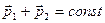(3.5)

Аналогично формуле (3.4) можно получить закон изменения импульса системы n материальных точек (тел):

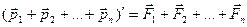(3.4а)

В отсутствие внешних сил соответственно будет справедлив закон сохранения импульса в изолированной системе n тел . Из него, в частности следует, что сумма импульсов Солнца, планет, астероидов и других тел Солнечной системы остается постоянной.

Понятие о тензоре инерции

Рассмотрим выражение в скобках в левой части уравнения (4.3а) или (4.4) - что то же самое. Это момент импульса системы материальных точек или момент импульса произвольного твердого тела, представленного такой системой точек. Будем считать, что центр декартовой системы координат совмещен с центром масс тела (рис 4.8), и в отличие от ранее рассмотренной задачи тело вращается произвольно вокруг центра масс, т.е. в разные моменты времени может вращаться вокруг разных осей вращения. При этом векторы момента импульса тела и угловой скорости могут быть неколлинеарными , т.е. не совпадать по направлению, даже в отсутствие внешних сил.

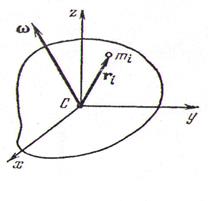
Рис 4.8. Произвольное вращение твердого тела.

Распишем момент импульса тела: 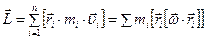- здесь мы скорость каждой материальной точки (элементарной массы) заменили векторным произведением угловой скорости тела на радиус-вектор точки – формула (3.2) и вынесли массу как скалярную величину за знак векторного произведения. Теперь воспользуемся формулой «бац минус цаб»: 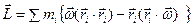. Напомним, что суммирование осуществляется по всем элементарный массам, на которые мысленно разбито тело. Скалярные произведения векторов в скобках выразим через сумму произведений их проекций на оси: ,

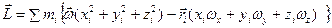где x_i , y_i , z_i – проекции радиус-вектора точки на оси координат (в данном случае координаты точки), w _x , w _y , w _z – проекции вектора угловой скорости тела.

Найдем проекцию этого вектора на ось х: =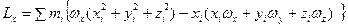

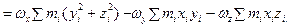
Аналогично находятся проекции вектора L на оси у и z :

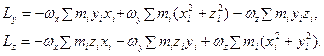
Теперь удобно записать связь момента импульса тела с его угловой скоростью в матричной форме:

L = Iw (4.13)

где L = 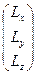- вектор момента импульса, w = 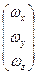- вектор угловой скорости, I = 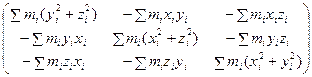- тензор инерции.

Тензор инерции – это квадратная матрица третьего порядка, и

перемножив тензор инерции и вектор угловой скорости по правилу

перемножения матриц, мы можем еще раз убедиться в правильности

формулы (4.13). Диагональные компоненты тензора представляют собой в соответствии с формулой (4.5) моменты инерции нашего тела относительно осей X , Y и Z . Эти компоненты называются осевыми моментами инерции. Недиагональные компоненты называются центробежными моментами инерции. Заметим, что недиагональные компоненты тензора удовлетворяют условию; 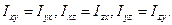Тензор, удовлетворяющий такому условию, называется симметричным. Записав тензор инерции с помощью компонент, получим более компактную форму:

I =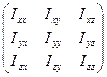

Надлежащим образом повернув декартову систему координат вокруг ее начала, т.е. вокруг центра масс тела, можно добиться того, чтобы все недиагональные компоненты тензора инерции стали равны нулю. В этом случае координатные оси совпадут с так называемыми главными осями инерции тела. При этом проекции того же вектора момента импульса будут выражены через проекции того же вектора угловой скорости следующим образом: 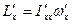, , 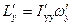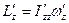. Все проекции и диагональные компоненты тензора инерции определены уже в новой системе координат.

Таким образом, у любого твердого тела есть три взаимно перпендикулярные оси, пересекающиеся в центре инерции, который у однородного тела любой формы совпадает с центром масс. Эти оси называются главными осями инерции. Моменты инерции тела относительно главных осей называются главными моментами инерции. В нашем случае 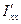, , 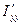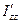- главные моменты инерции. Если тело вращается вокруг любой из своих главных осей инерции, то, как следует из (4.13), его вектора момента импульса и угловой скорости коллинеарны, т.е. совпадают по направлению. При этом, если на тело не действуют моменты внешних сил, такая ось вращения, будучи незакрепленной, остается неподвижной во время вращения.

Гироскоп

Гироскопом называется симметричное массивное тело, вращающееся вокруг оси симметрии, совпадающей с одной из главных осей инерции. Угловая скорость вращения w достаточно велика. Как было сказано в предыдущем параграфе, в отсутствие моментов внешних сил эта ось вращения будет оставаться неподвижной, а вектора момента импульса L и угловой скорости w будут совпадать по направлению.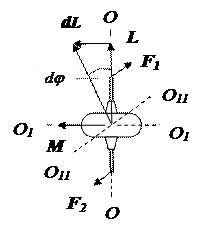

Рис. 4.9. Поворот оси гироскопа под действием внешних сил F ₁ и F ₂.

Приложим к оси гироскопа ОО пару сил F ₁ и F ₂, параллельных оси О₁₁О₁₁ (рис. 4.9). Эта ось перпендикулярна плоскости рисунка.

Казалось бы, ось гироскопа должна повернуться вокруг оси О₁О₁ , однако она поворачивается вокруг оси О₁₁О₁₁ за время dt на угол d j . Это происходит в согласии с законом изменения момента импульса (4.3) или (4.3а). В нашем случае его удобно записать с помощью дифференциалов: dL=Mdt (1) , где dL – изменение (дифференциал) вектора момента импульса, M – момент пары сил F ₁ и F ₂ – на рисунке вектор момента сил лежит на оси О₁О₁. Радиус-векторы этих сил выходят из центра гироскопа - на рисунке они не показаны. Момент пары сил определяется как сумма моментов каждой силы или как удвоенный момент любой из них, так как и радиус-векторы, и силы равны по модулю.

При малых углах d j , как видно из рисунка, dL / L = tgd j » d j. С другой стороны, по определению (3.1): d j / dt = w ₁ , где w ₁ – модуль угловой скорости поворота вектора L . Таким образом, с учетом равенства (1) получим: w ₁=M / L (2). Обычно w ₁<<w , поэтому ось гироскопа в таких случаях в любой момент времени совпадает с вектором момента импульса гироскопа. Таким образом, в результате действия пары сил гироскоп действительно повернется вокруг оси О₁₁О₁₁. Вектора w ₁ , M , L связаны аналогичным равенству (2) векторным соотношением: M =[w ₁ L] (4.14)

Соответственно, модуль вектора M в общем случае равен:

M = w ₁ Lsin a (4.15)

где a - угол между векторами w ₁ и L (в нашем случае он равен 90 градусам).

Рассмотрим гироскоп в поле силы тяжести. Ось гироскопа шарнирно закреплена в точке О (рис. 4.10). Модуль вектора момента силы тяжести, приложенного к гироскопу, равен:

M = mglsin a (4.16)

где m – масса гироскопа, l – расстояние от точки О до центра масс

гироскопа, 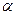- угол, образованный осью гироскопа с вертикалью. Направлен вектор M перпендикулярно вертикальной плоскости, проходящей через ось гироскопа (на рисунке эта плоскость заштрихована). За время dt вектор момента импульса гироскопа получит приращение: dL=Mdt . Соответственно этому приращению переместится ось гироскопа . Вектор dL таким образом в любой момент времени будет перпендикулярен каждому предыдущему положению оси гироскопа. Ось гироскопа будет поворачиваться вокруг вертикали,

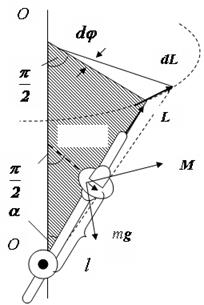
Рис. 4.10. Прецессия гироскопа в поле силы тяжести.

описывая конус с углом при вершине, равным 2 a. Такое движение гироскопа называется прецессией. Угловую скорость прецессии w ₁ можно найти из (4.15) и (4.16): w ₁=mgl / L .

Глава 5. Колебания

5.1. Гармонические колебания без трения

Гармоническим колебанием материальной точки является такое ее движение, при котором смещение точки от положения равновесия зависит от времени по закону синуса или косинуса. Рассмотрим шарик массой m, висящий на пружине жесткостью к (рис. 5.1).

Рис. 5.1. Шарик, висящий на пружине – начало оси Х совпадает с положением равновесия шарика.

Сместим шарик вниз на расстояние 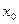и отпустим его, одновременно включив секундомер. Применим к шарику второй закон Ньютона в проекции на ось Х: 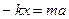, где kx – сила упругости, х – в нашем случае координата шарика. Мы не учитываем равные по величине и противоположные по знаку проекции силы тяжести и части силы упругости. Так как 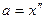, то последнее уравнение можно записать в виде: 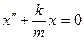. Обозначив: 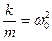(5.1)

получим стандартное дифференциальное уравнение колебаний точки:

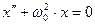(5.2)

Решением этого дифференциального уравнения является функция:

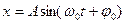(5.3)

которая определяет координату шарика х в любой момент времени t . В формуле (5.3): А – амплитуда колебаний шарика, м

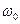- циклическая частота, рад/с

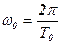, Т₀ – период колебаний, с

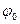- начальная фаза, рад

Взяв первую и вторую производные, получим соответственно выражения для скорости и ускорения:

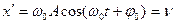(5.3а) 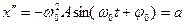(5.3б)

Определим A и 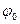для нашего конкретного случая из начальных условий колебаний: при t=0 координата шарика x=x₀, начальная скорость 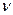=0. Подставив эти величины в (5.3) и (5.3а), получим систему уравнений:

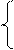
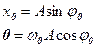
Решая вначале второе уравнение, получим 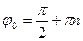, n=0,±1,... Подставив выражение для начальной фазы в первое уравнение, придем к значениям амплитуды и начальной фазы: 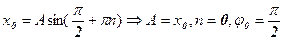. Таким образом, зависимость координаты нашего шарика от времени имеет следующий вид: 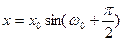. В данном случае амплитуда равна начальному смещению шарика от положения равновесия. Графики смещения (координаты) и скорости шарика от времени приведены на рисунках (5.2) и (5.3).

Т₀

Рис. 5.2. График зависимости смещения колеблющейся точки от времени.

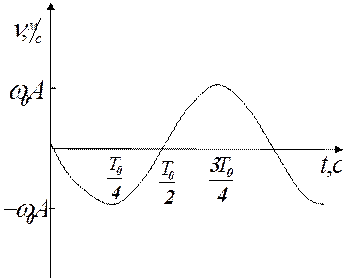
Рис. 5.3. График зависимости скорости колеблющейся точки от времени.

Физический маятник

Физическим маятником называется произвольное твердое тело, закрепленное на оси, не проходящей через центр масс, и способное совершать колебания относительно положения равновесия (рис 5.4). В положении равновесия отрезок СО лежит на вертикали. Если отклонить физический маятник на угол j, то появится момент силы тяжести и после отпускания маятника, он начнет совершать колебания. Определим период этих колебаний, считая угол j достаточно малым. Момент силы тяжести равен: М=- mglsin j , знак минус вызван тем, что момент силы и угол поворота в нашем случае имеют противоположные знаки.

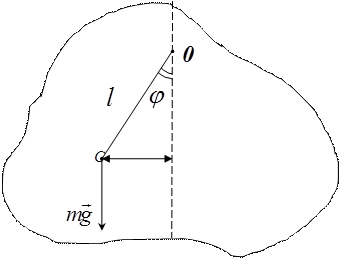
Рис 5.4. Колебания физического маятника. С- центр масс; m- масса тела; О – точка, через которую проходит горизонтальная ось; 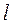- расстояние между центром масс и осью крепления.

Из основного уравнения динамики вращательного движения: M = I b , где I – момент инерции физического маятника относительно оси крепления, b - угловое ускорение маятника, равное второй производной угла поворота: 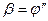, и с учетом того, что при малых углах sin j = j, получим: 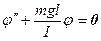. Обозначив 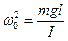, придем к стандартному дифференциальному уравнению

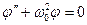(5.4), аналогичному (5.2). Это означает, что при отсутствии сил трения и сопротивления физический маятник будет совершать такие же гармонические колебания, как и шарик на пружине, с циклической частотой w ₀ и соответственно с периодом:

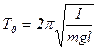(5.5)

Из формулы (5.5) можно получить формулу для периода математического маятника. Математический маятник – материальная точка на невесомой нити длиной 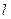. Момент инерции материальной точки (4.5): 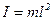. Подставив его в (5.5), получим формулу для периода колебаний математического маятника:

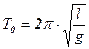(5.5а)

Глава 6. Волны

В стальном круглом стержне

Рассчитаем теоретически скорость продольной волны в тонком стальном стержне. Для этого нам потребуются некоторые сведения из теории упругости. Закон Гука:

s = E e (6.7)

где s - механическое напряжение действующее в образце под действием некоторой внешней силы F, Н/м², s = F / S, где S – площадь сечения образца, м², E – модуль упругости (модуль Юнга) материала, из которого изготовлен образец, Н/м², e - относительная деформация образца под действием внешней силы F, e = D L / L ₀, где L ₀ – первоначальная длина образца, D L – абсолютное удлинение ( укорочение) образца. e - величина безразмерная (м/м).

Рассмотрим стержень, в котором распространяется продольная волна в направлении от его свободного конца к закрепленному, т.е. в положительном направлении оси Х (рис.6.3). По аналогии со

Рис.6.3.Распространение продольной волны в круглом стальном стержне. Длина стержня l много больше его диаметра d (l > > d).

связанными маятниками сечения стержня в процессе распространения волны начнут вовлекаться в колебательное движение относительно

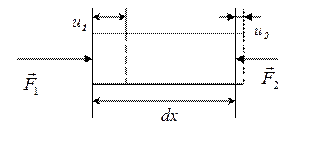
Рис. 6.4. Элементарный участок стержня в процессе распространения волны. u ₁ и u ₂ – смещения левого и правого сечений участка, F ₁ и F ₂ – силы, действующие на рассматриваемый участок со стороны соседних участков.

своего положения равновесия. Поскольку волна продольная, колебания сечений стержня будут происходить вдоль оси Х . Выделим элементарный участок стержня длиной dx (рис. 6.4).

Применим к этому участку стержня второй закон Ньютона в проекции на ось Х: 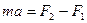, , 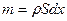где 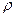- плотность стали, S – площадь сечения стержня, 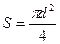. Ускорение участка стержня – это вторая производная смещения участка по времени (частная производная, так как смещение есть функция двух переменных: времени t и координаты х): 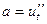. Силы 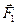и 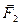выразим через закон Гука: , .

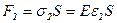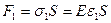В итоге получим: 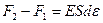, где d e = e ₂ - e ₁ - дифференциал относительной деформации участка стержня (в первом приближении дифференциал равен приращению). Дифференциал функции, как известно из курса высшей математики, равен производной функции, умноженной на дифференциал аргумента: 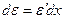. В нашем случае относительная деформация равна 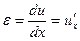, т.к. du = u ₂ - u ₁ – это абсолютное удлинение участка, а dx – первоначальная длина участка. Поэтому 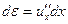. Всё это подставим в выражение для второго закона Ньютона, получим: 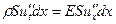. Сокращая на площадь сечения участка и его первоначальную длину, запишем предыдущее выражение в следующем виде:

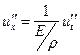(6.8)

Сравним (6.8) с известным из теории волн дифференциальным уравнением плоской волны распространяющейся вдоль оси Х (уравнением Лапласа):

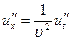. (6.9)

Получим, что скорость распространения продольной волны в тонком стержне равна: 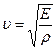(6.10)

Так как модуль Юнга стали равен 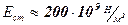, а плотность стали 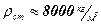то скорость продольной волны в стержне равна 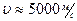. Кстати, решением уравнения Лапласа (6.9) является уравнение плоской волны (6.2) .

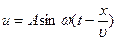К главе 1

1. Объясните, почему из определения скорости следует, что вектор скорости всегда направлен по касательной к траектории.

2. Что получится, если умножить вектор на число: большее единицы, меньшее единицы, отрицательное, ноль? Объясните смысл введения единичного вектора скорости.

3. Найдите разность единичных векторов скорости Δе на рис. 1.3. К чему она стремится по модулю и по направлению при бесконечном уменьшении промежутка времени Δ t?

4. Как определить основание равнобедренного треугольника, зная длину боковой стороны и угол при вершине этого треугольника?

5. Производная модуля скорости – это векторная или скалярная величина? Чему равна производная модуля скорости точки, движущейся равномерно по окружности?

6. Чему равна производная единичного вектора скорости точки, движущейся равномерно по окружности?

7. Как по отношению к траектории движения точки направлены векторы ее тангенциального и нормального ускорений (рис.1.4)?

К главе 2

8. Если вектор с равен векторному произведению вектора а на вектор b, то как выразить проекции вектора с через проекции векторов а и b?

9. Вектор с равен векторному произведению вектора а на вектор b. Последние два вектора, находясь в плоскости рисунка, выходят из одной точки, причем вектор а направлен вверх, а вектор b - вправо. Как по отношению к плоскости рисунка направлен вектор с?

10. Как можно выразить радиус-вектор точки А через вектор ρ и чему равна производная по времени вектора ОО₁ ?

11. Какие свойства предела и в каком месте использованы при выводе выражения для модуля скорости точки А ?

12. Как записывается векторное произведение, если один из перемножаемых векторов является суммой двух, трех и т.д. векторов, и где это применяется в данной главе?

13. Объясните применение формулы “бац минус цаб” для получения нормального ускорения точки А в формуле (2.4).

14. Используя рисунки 1.4 и 2.2 и правила векторного умножения векторов объясните, почему формула (2.4) эквивалентна формуле (1.3б).

К главе 3

15. Чем отличается вектор импульса тела от вектора скорости тела?

16. Следствием каких законов является закон изменения импульса?

17. Почему можно заменить тело системой материальных точек и почему эта система не распадается в процессе движения?

18. Перечислите по порядку все математические операции , применяемые в процессе вывода формулы (3.6).

19. Объясните, почему из формулы (3.6) следует, что центр масс движется с ускорением свободного падения.

20. Как иначе можно назвать проекции радиус-вектора точки на оси координат?

21. Докажите математически, что центр масс двух любых материальных точек находится на отрезке, соединяющем эти точки.

22. Перечислите все принципиальные отличия скалярного произведения двух векторов от их векторного произведения.

23. Как приблизительно определить работу по формуле (3.9), если траектория точки вычерчена на миллиметровке в масштабе, и при необходимости , для каждой точки траектории можно построить вектор силы в необходимом масштабе. Как вы понимаете масштаб для вектора силы?

24. Что такое дифференциал функции, дифференциал аргумента и как они связаны? Где и как это применяется в доказательстве теоремы о кинетической энергии?

25. Чему равно скалярное произведение вектора на самого себя и где это применяется в доказательстве теоремы о кинетической энергии?

26. Найдите частные производные функции u = x ² yz + sin (2 x +3 y +4 z ).

27. Объясните с помощью рисунка 3.5, почему у вектора силы тяжести такие проекции.

28. Чему равен определенный интеграл полного дифференциала функции нескольких переменных и чем отличается в этом смысле полный дифференциал от дифференциала функции одного переменного?

29. Почему из (3.10) и (3.12) следует закон сохранения механической энергии (3.13)?

30. С помощью формулы (3.14) и правила векторного умножения векторов объясните рисунок 3.7.

К главе 4

31. Как направлен вектор момента импульса на рисунке 4.1 и вектора моментов силы на рисунке 4.2?

32. Как направлен вектор разности радиус-векторов материальных точек m ₁ и m ₂ на рисунке 4.3, и чему равен модуль этого вектора?

33. Объясните направление осей τ , ρ и z на рисунке 4.4.

34. Если предположить, что сила F не действует, то как будут направлены силы реакции подшипников и фланца на ось на рисунке 4.4?

35. Как изменится сила реакции фланца N ₂ после начала действия силы F (см. рис. 4.4)?

36. Почему первая сумма, получившаяся после преобразования левой части уравнения (4.4), является суммой векторов, перпендикулярных оси вращения?

37*. Покажите, что первая сумма, получившаяся после преобразования левой части уравнения (4.4), есть вращающийся вектор. Как он направлен по отношению к телу и как направлена его производная?

38*. Что происходит с векторами сил реакции подшипников на ось при вращении тела на рисунке 4.4?

39. Какие из шести векторных произведений, получившихся после преобразования момента силы F . параллельны оси вращения, перпендикулярны ей и равны нулю?

40. Как обобщить формулу (4.7) на случай действия двух, трех и т.д вращающих сил?

41. Объясните разницу в выводе формул (4.10а) и (4.10б).

42. Объясните, чему препятствует сила трения покоя, действующая на цилиндр на наклонной плоскости (рис. 4.7).

43. Чему равно плечо силы тяжести, действующей на цилиндр (рис.4.7)?

44. Объясните, по какой формуле из главы 2 и как получено выражение для углового ускорения цилиндра относительно мгновенной оси вращения (рис.4.7).

45. Объясните, откуда получено выражение для силы трения скольжения на цилиндр (рис.4.7).

46. Проверьте правильность формулы (4.13) путем непосредственного перемножения матриц.

47. Докажите, что при вращении произвольного тела вокруг любой из его главных осей инерции, вектора момента импульса и угловой скорости будут коллинеарны.

48. Как направлен вектор dL гироскопа и почему?

49. Докажите, используя рисунок 4.9, определение вектора угловой скорости и правило векторного перемножения векторов, справедливость формулы 4.14.

50. Объясните, как должны быть направлены радиус-векторы каждой из пары сил, действующих на гироскоп, и почему момент этой пары сил направлен именно так, как это показано на рисунке 4.9?

51. Объясните, как направлен вектор момента силы тяжести, действующей на гироскоп?

К главе 5

52. Проверьте подстановкой, что функция (5.3) является решением дифференциального уравнения (5.2).

53. Объясните с помощью рисунков 5.2 и 5.3, как меняется скорость и координата шарика в течение одного периода колебаний.

54. Если шарик подвешен на пружине, которая работает только на растяжение (в недеформированном состоянии витки пружины прижаты вплотную друг к другу), то какими факторами ограничивается величина начального смещения х₀ .

55. Сравните дифференциальные уравнения (5.2) и (5.4). Какая функция будет являться решением уравнения (5.4)?

56. Определите знак проекций силы Стокса, силы упругости, скорости, ускорения, знак координаты колеблющегося шарика в какой – нибудь момент времени.

57. Если шарик сместили от положения равновесия на х₀ , а потом отпустили, включив секундомер, то каковы будут величины А₀ и φ₀ в формуле (5.7) ?

58*. Куда направлен вектор равнодействующей сил тяжести и Архимеда, действующих на колеблющийся с трением шарик? Объясните, откуда берется часть силы упругости, уравновешивающая эту равнодействующую, когда шарик проходит верхнюю точку. Считайте, что пружина может работать только на растяжение (в недеформированном состоянии витки пружины прижаты вплотную друг к другу).

59. В каких случаях и в какой момент времени смещение шарика будет равняться А₀ (см. формулу 5.7) ?

60. В чем измеряется коэффициент затухания β ?

61. Объясните, как из рисунка 5.8 получить формулу (5.13) ?

62. Определите, какой вектор на векторной диаграмме (рис. 5.8) соответствует координате, скорости и ускорению шарика и чему равны максимальные значения этих величин. В какой последовательности удобнее складывать эти три вектора и почему?

63. Определите наименьшее значение коэффициента затухания β , при котором резонанс не возникает. Примите m=100 кг, k=10000Н/м.

К главе 5

64. Какие тригонометрические формулы и как использованы в параграфе 6.2 ?

65. Проверьте подстановкой, что функция (6.2) является решением уравнения Лапласа (6.9).

66*. Продольная волна в стержне начинает распространяться после горизонтального удара справа по незакрепленному концу стержня. Если предположить, что затухание в стержне отсутствует, то как распределится часть энергии удара, перешедшая в энергию волны, в течение времени, необходимого для достижения волной закрепленного конца?

67. В конце главы 6 сравниваются: механическая энергия волны и колеблющегося шарика. Что при этом подразумевается под потенциальной энергией шарика и почему?

Литература

1. Д.В.Сивухин. Общий курс физики. Том 1. Механика – Москва, Наука, 1990.

2. И.В.Савельев. Курс общей физики. Том 1. Механика. Молекулярная физика – Москва, Наука, 1977.

3. А.А. Детлаф, Б.М. Яворский. Курс физики – Москва, Высшая школа, 1989.

Словарь терминов

1. Материальная точка – это твердое тело, размеры и форма которого в рассматриваемой задаче несущественны. Поэтому всю массу тела приписывают какой-нибудь одной его точке, обычно центру масс, и в дальнейшем рассматривают только эту точку.

2. Вектор – это значение векторной физической величины, например силы, выраженное в виде направленного отрезка определенной длины. Длина вектора пропорциональна в данном случае числу ньютонов, а направление указывает направление этой силы.

3. Система отсчета – это часы (секундомер) и декартова система координат, связанная с выбранным телом.

4. Радиус-вектор точки – это вектор, начало которого совпадает с началом координат, а конец – с самой точкой.

5. Координаты точки – это проекции на оси ее радиус-вектора. Координаты точки, равно как и радиус-вектор, однозначно определяют положение точки в пространстве.

6. Проекция вектора на ось – это длина отрезка на оси, взятая со знаком плюс или минус в зависимости от угла между вектором и осью. При этом концы данного отрезка совпадают с основаниями перпендикуляров, опущенных на ось из концов вектора.

7. Перемещение точки – это вектор, соединяющий начальное и конечное положение точки.

8. Скорость точки – вектор, касательный к траектории точки, длина которого пропорциональна величине скорости, а направление совпадает с направлением движения точки.

9. Потенциальная энергия – это энергия, обусловленная либо взаимодействием частей тела между собой, например: потенциальная энергия деформированной пружины или деформированного тела, либо взаимодействием тела с другими телами, например: потенциальная энергия тела в поле силы тяжести Земли. Вообще, энергия тела или системы – это возможность для этого тела или системы при определенных условиях совершить работу.

10. Механическое напряжение, действующее в сечении образца (в нашем случае стержня) – это отношение силы, приложенной к данному сечению, к площади сечения.

11. Модуль Юнга – это коэффициент пропорциональности между механическим напряжением в образце и относительной деформацией образца.

Содержание

Введение……………………………………………………………….....5

Механика твердого тела

Глава 1. Кинематика поступательного движения……………………..7

1.1. Скорость и перемещение точки………………………………..7

1.2. Нормальное и тангенциальное ускорения…………………….8

Глава 2. Кинематика вращательного движения……………………..10

2.1. Векторы угла поворота, угловой скорости и ускорения…….10

2.2. Связь линейных и угловых величин ……………………….....12

Глава 3. Динамика поступательного движения.

Законы сохранения……………………………………………...14

3.1. Инерциальные системы. Законы Ньютона…………………....14

3.2. Закон изменения импульса………………………………….....15

3.3. Центр масс произвольного тела……………………………….16

3.4. Работа переменной силы. Кинетическая энергия……………..18

3.5. Потенциальные силы, потенциальная энергия.

Закон охранения механической энергии ……………………..20

3.6. Неинерциальные системы отсчета……………………………...22

Глава 4. Динамика вращательного движения…………………………..24

4.1. Момент импульса, момент силы………………………………...24

4.2. Закон изменения момента импульса системы

материальных точек……………………………………………..26

4.3. Вращение произвольного твердого тела

вокруг закрепленной оси………………………………………..27

4.4. Моменты инерции различных тел. Кинетическая

энергия вращающегося тела………………………………….....31

4.5. Применение законов динамики вращательного движения….....33

4.6. Понятие о тензоре инерции………………………………………34

4.7. Гироскоп…………………………………………………………...37

Механические колебания и волны

Глава 5. Колебания………………………………………………………...40

5.1. Гармонические колебания без трения……………………………40

5.2. Физический маятник………………………………………………43

5.3. Колебания в системе с трением………………………………….44

5.4. Вынужденные колебания в системе с трением………………….46

Глава 6. Волны……………………………………………………………..50

6.1. Колебания связанных маятников………………………………...50

6.2. Продольные и поперечные волны. Фронт

волны. Длина волны. Интерференция волн……………………51.

6.3. Скорость распространения продольной волны в стержне……..53

6.4. Энергия волны. Плотность энергии……………………………..56

Вопросы для самостоятельной работы…………………………………..58

Литература………………………………………………………………64

Словарь терминов……………………………………………………….65

Введение

Механика твердого тела

Дата: 2018-11-18, просмотров: 294.

12 3 4 5 6 7 8 9 10 Следующая ⇒