На ортогональном чертеже любой многогранник может быть задан проекциями его вершин, ребер и граней.

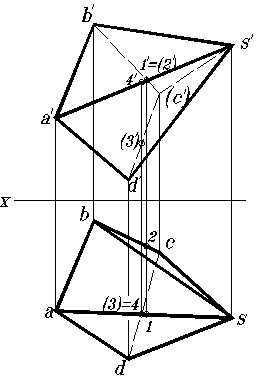
На рис. 118, а показан пример выполнения чертежа пирамиды, основания и грани которой занимают общее положение.

Вершины многогранника заданы точками А, В, С, D и S , ребра – отрезками прямых АВ, ВС, СА, AD , AS , BS , DS и CS , а грани – треугольниками, основание – четырехугольником ABCD.

Видимость ребер и граней многогранника на ортогональном чертеже определяется с помощью следующих правил.

1. Проекции ребер, которые образуют внешний контур проекции многогранника, всегда видны.

2. Видимость остальных ребер определяется методом конкурирующих точек. Например, на рис. 6.4 видимость на фронтальной плоскости определяется по горизонтальной проекции многогранника. Сравниваем ординаты конкурирующих точек I и II: y₁ > y₂. Точка I и ребро AS, на котором она находится, расположены ближе, чем точка II и ребро BC . Значит, ребро AS на фронтальной плоскости будет видимым, а ребро BC – нет. Для установления видимости на горизонтальной плоскости можно рассмотреть конкурирующие точки III и IV.

3. Грань многогранника видна, если видны все ее ребра.

4. Грань не видна, если не видно хотя бы одно ее ребро.

Выбирая положение призмы или пирамиды для изображения, целесообразно их основания располагать параллельно плоскости проекций. Чертеж наклонной призмы с треугольными основаниями, параллельными горизонтальной плоскости проекций Н, показан на рис. 118, б. Чертеж треугольной пирамиды с основанием, лежащим в плоскости Н, приведен на рис. 118, в.

                                                                                      а

                 б                                                             в

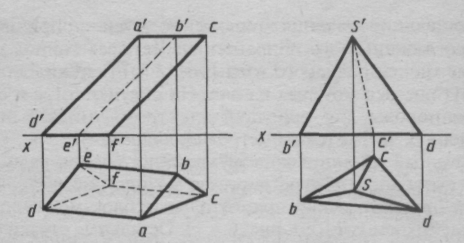
Рис. 118. Ортогональные проекции многогранника

Недостающие проекции точек на поверхности призм и пирамид строятся по их принадлежности ребрам и граням.

На рис. 119 показаны проекции шести- и треугольной призм. Так как они занимают горизонтально-проецирующее положение, то все точки, принадлежащие боковым граням, на горизонтальной плоскости проекций будут проецироваться на след – шестиугольник (рис. 119, а) и треугольник (рис. 119, б). Профильные проекции а" и с" построены с помощью координат y_A  и y_C, определяемых по горизонтальным проекциям.

Если нужно на проекциях многогранника построить точку, лежащую на одной из граней, занимающей общее положение, то следует связать точку с этой гранью при помощи какой-либо прямой, принадлежащей ей. Например, горизонтальная и профильная проекции точки D на грани S–1–2 пирамиды (рис. 120, а) построены с мощью отрезка 2–4 этой грани. Аналогично с помощью отрезка 1–5 на грани S–1–2 пирамиды (рис. 120, б) построена профильная проекция точки f ". Горизонтальная проекция f определена с помощью горизонтали той же грани, проходящей через точку 6 на ребре S1. Горизонтальная проекция точки е построена с помощью координаты y_E, установленной по профильной проекции е".

В рассмотренных примерах координаты y заданы относительно плоскостей уровня R и Т.

            а                                                                б

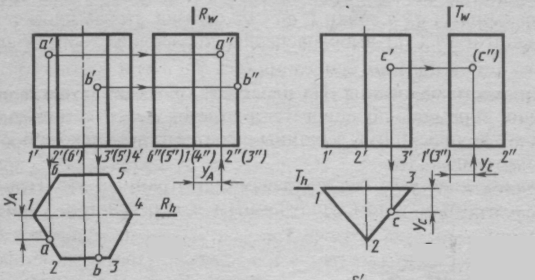
Рис. 119. Определение точек на поверхности призмы

а                                                                 б

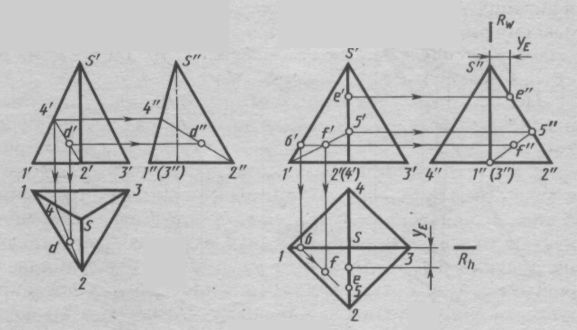
Рис. 120. Определение точек на поверхности пирамиды