Решение:

Анализируем графическое условие задачи:

 заданная плоскость занимает общее положение в пространстве. Следовательно, для определения натуральной величины плоскости треугольника необходимо осуществить два преобразования:

1. Преобразовываем заданную плоскость в проецирующую.

2. Преобразовываем заданную плоскость в плоскоть уровня.

     Порядок выполнения графической части задачи (рис. 108):

1. Так как по условию задачи необходимо найти угол наклона плоскости треугольника к горизонтальной плоскости проекций, заданную плоскость преобразуем во фронтально проецирующую. Условия ввода плоскости V₁: V₁ ⊥ H, V₁ ⊥ ∆DВ A.

1.1. Анализируем положение отрезков прямых, которыми задана плоскость треугольника: все они занимают общее положение.

1.2. Проводим в заданной плоскости горизонталь А N .

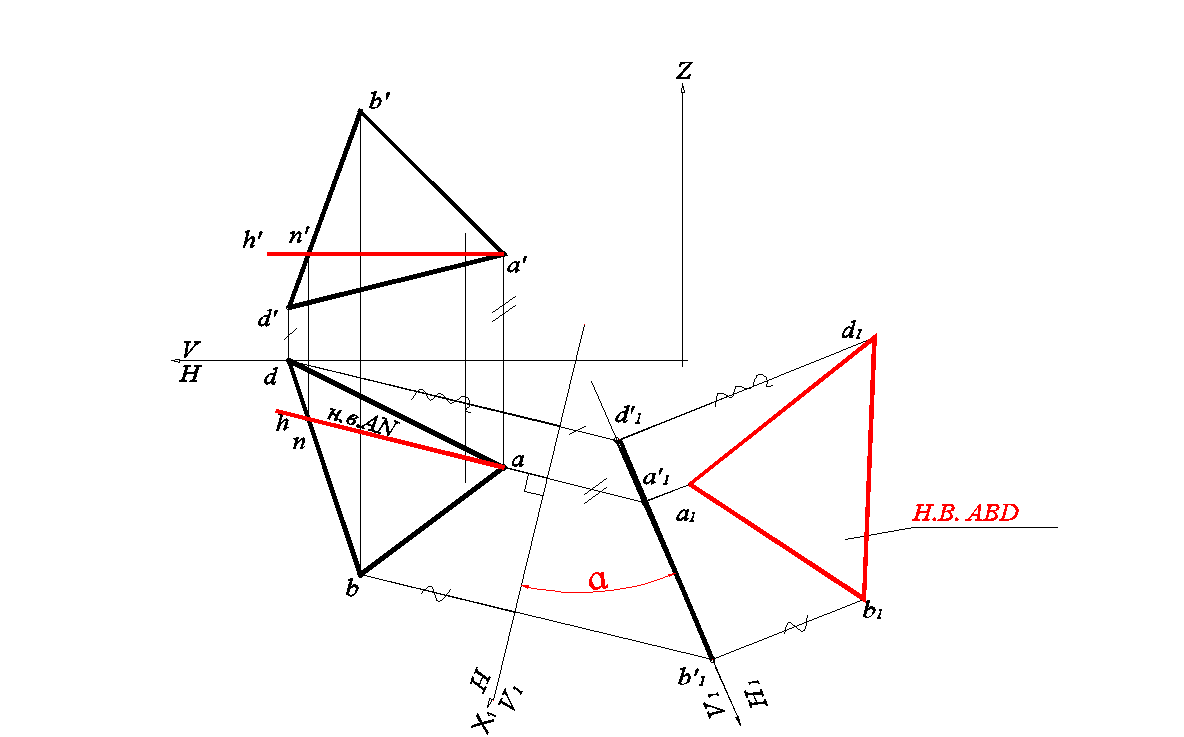
Рис. 108. Определение натуральной величины плоскости ∆АВ D

1.3. Перпендикулярно горизонтальной проекции горизонтали проводим новую ось проекций Х₁ на любом расстоянии от точки А.

1.4. Откладываем от оси Х₁ координаты Z_D, Z_B, Z_C вдоль линии связи точек В, С и D.

1.5. Получаем проекцию плоскости ∆DВ A в виде прямой линии.

1.6. На новую плоскость проекций V₁ плоскость ∆DВ A отобразилась в впрямую линию, т. е. стала фронтально проецирующей плоскостью. На новой плоскости проекций V₁ угол наклона плоскости треугольника DВ A к горизонтальной плоскости проекций α отображен без искажения.

2. Для построения натуральной величины плоскости треугольника преобразовываем ее в горизонтальную плоскость уровня.

2.1. Вводим новую плоскость проекции Н₁: V₁ ⊥ H₁, Н₁ || ∆DВ A.

2.2. Ось проекции X₂ – горизонтальный след плоскости Н₁. Проводим параллельно прямой b₁′d₁′a₁′ ось X₂ на любом расстоянии от нее.

2.3. Проводим из точек b₁′, d₁′, a₁′ линии связи (перпендикуляры к оси X₂).

2.4. Откладываем расстояния от точек а, b и d до оси Х₁ по линиям связи этих точек от X₂ соответственно точкам A, B, D.

2.5. Получаем точки a₁, b₁, d₁. Соединяя полученные точки, получим новую проекцию плоскости ∆DВ A равную натуральной величине ∆DВ A .

Следовательно, в новой системе плоскостей плоскость занимает положение горизонтальной плоскости уровня.

Метод вращения

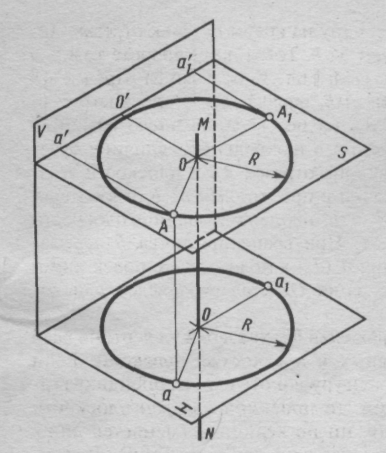
Суть метода заключается в том, что геометрический элемент вращается (перемещается) относительно неподвижных плоскостей проекций, занимая необходимое частное положение. Каждая точка вращаемого элемента перемещается в плоскости (плоскость вращения) перпендикулярной к некоторой неподвижной прямой (оси вращения) по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (радиус вращения).

Итак, для применения способа вращения в целях преобразования чертежа отметим следующие четыре элемента (рис. 109): ось вращения MN; плоскость вращения точки S _┴ MN; центр вращения S ∩ MN = О; радиус вращения R = | OA |.

Рис. 109.  Вращение точки вокруг оси

В качестве оси вращения обычно используют прямые, перпендикулярные или параллельные плоскостям проекций. Кроме того, ось может быть задана или выбрана, указана или нет. В зависимости от этого рассматривают различные способы:

– вращение вокруг оси, перпендикулярной к плоскости проекций;

– вращение без указания осей вращения или плоскопараллельное перемещение;

– вращение вокруг прямых, параллельных плоскости проекций;

– вращение плоскости вокруг следа (метод совмещения).