Экватор и все меридианы сферы имеют одинаковые диаметры. Параллели же будут иметь разные диаметры. Чем ближе к экватору, тем больше диаметр параллели, и наоборот.

Сфера (шар) на ортогональных и прямоугольных аксонометрических проекциях изображается как круг (рис. 143). Очерковой линией сферы будет окружность.

В прямоугольной изометрической проекции диаметр очерковой окружности в соответствии с ГОСТ 2.317–2011 составляет 1,22, а прямоугольной диметрической проекции 1,06 диаметра сферы. Для наглядности в аксонометрии на поверхности полной сферы показывают экватор и два главных меридиана (рис. 142).

На трех ортогональных проекциях диаметры очерковых окружностей одинаковые и равны диаметру сферы (рис. 143).

В ортогональных проекциях на горизонтальной плоскости проекций очерковой линией сферы будет экватор, который на фронтальную плоскость проекций проецируется в отрезок, совпадающий с центровой линией а на профильной проекции проекция экватора также совпадает с центровой линией. На фронтальной плоскости проекций очерковой линией сферы будет фронтальный меридиан, а на профильной – профильный меридиан.

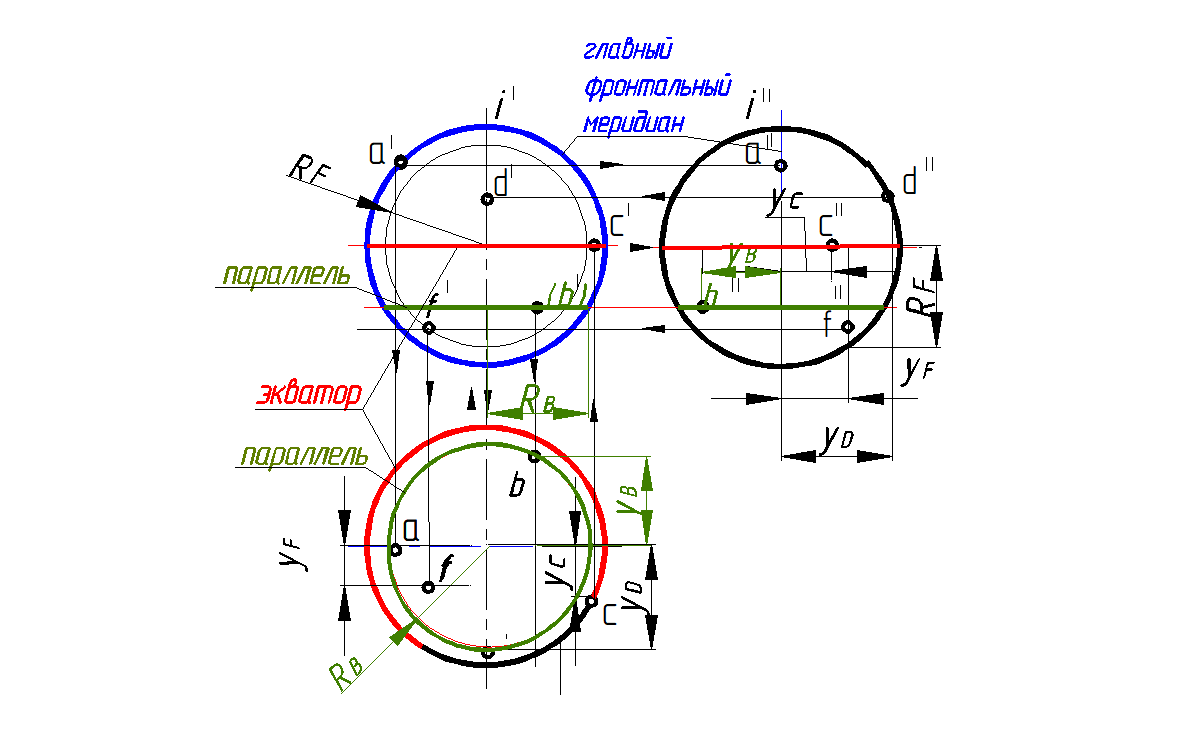
Рис. 143.Сфера в ортогональных проекциях

Эллипсоид вращения – образующей является эллипс; осью вращения может быть большая (рис. 144, а) и малая оси эллипса (рис. 144, б).

а                                                               б

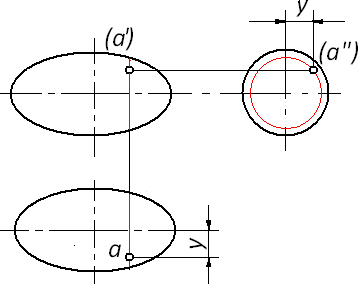
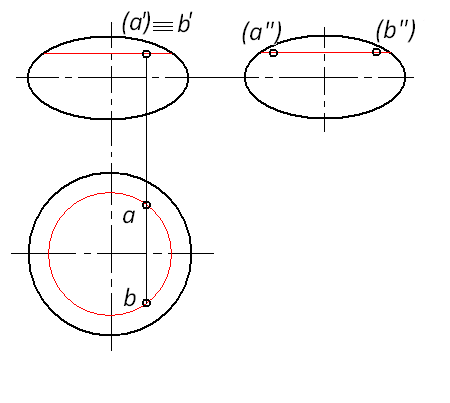
Рис. 144. Эллипсоид вращения:

а – осью вращения является большая ось эллипса;

б – осью вращения является малая ось эллипса

Параболоид образуется вращением параболы вокруг ее оси (рис. 145).

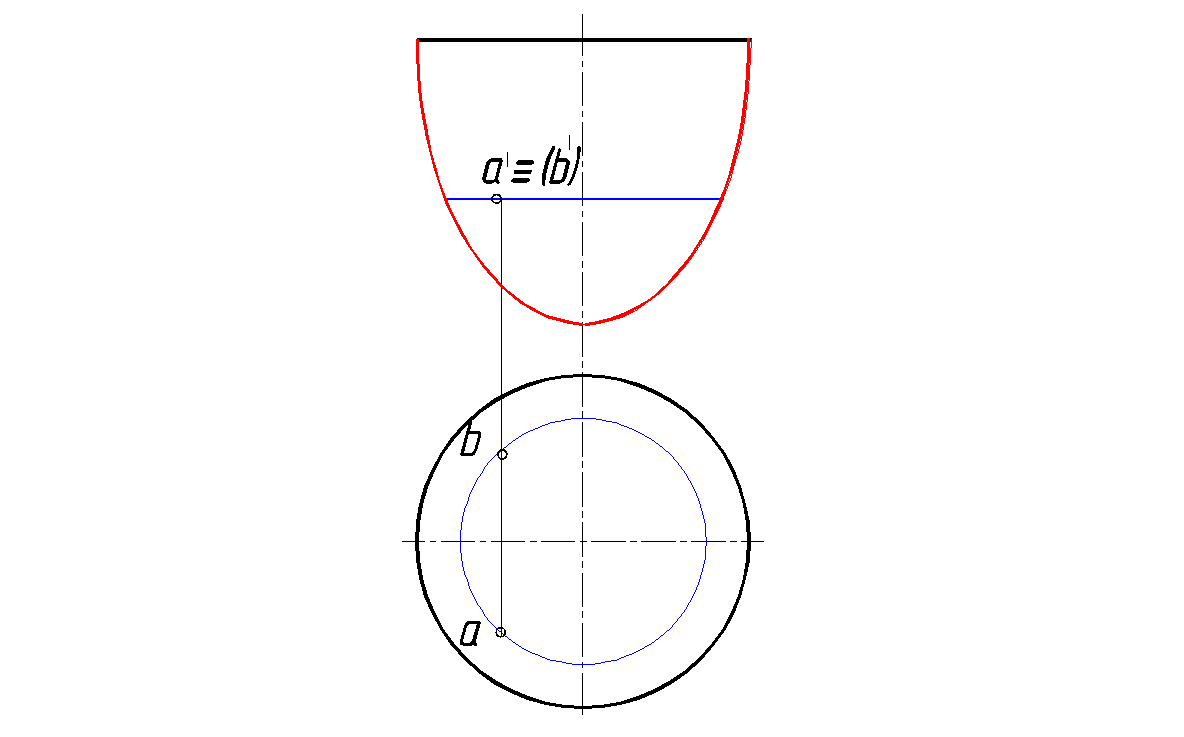
Рис. 143. Параболоид вращения

Гиперболоид – образуется вращением гиперболы вокруг ее мнимой или действительной оси, при этом, если за ось вращения принять мнимую ось, получим однополостный гиперболоид вращения (рис. 144, а), а если действительную ось – двуполостный гиперболоид вращения (рис. 144, б).

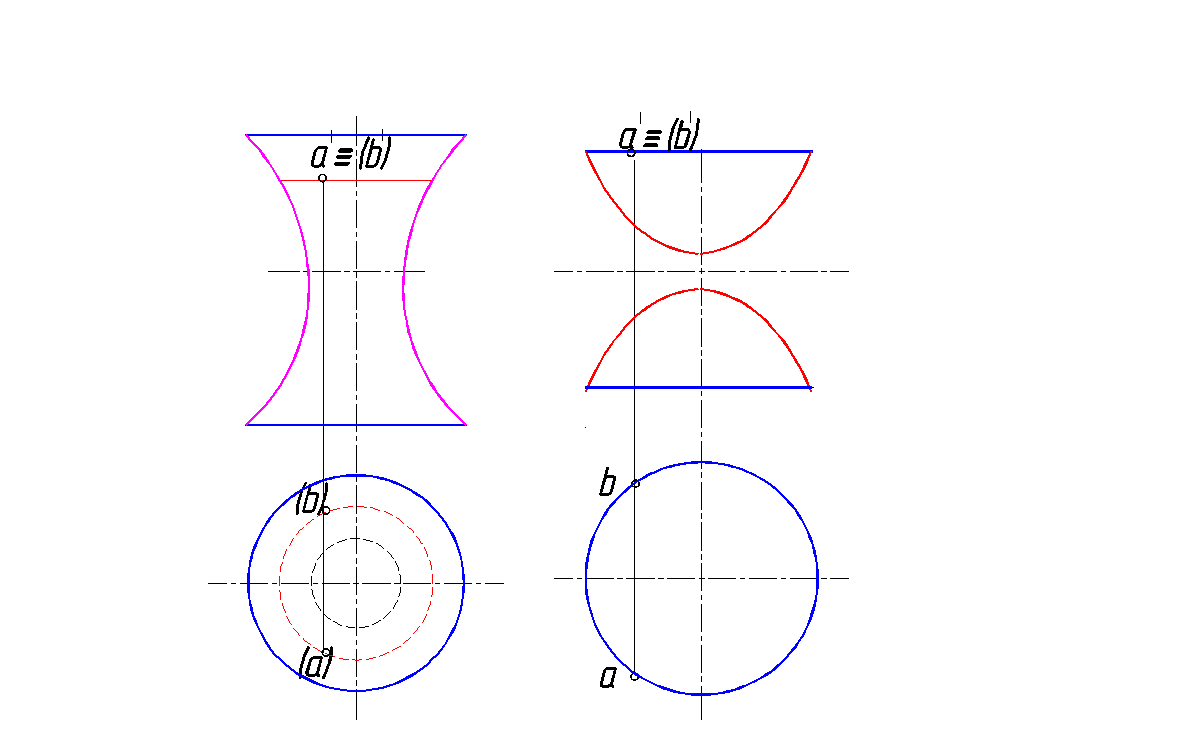
 Рис. 144. Гиперболоид:

а – однополостный; б – двуполостный

Цилиндрическая и коническая поверхности вращения являются частным случаем линейчатых развертываемых поверхностей, рассматриваемых выше.

Это поверхности 2-го порядка, но их образующая – прямая. Эти поверхности образуются при вращении прямой линии вокруг оси. При этом если образующая параллельна оси, то образуется цилиндрическая поверхность (рис. 145), если пересекается с осью – коническая (рис. 146). Для них меридианы являются прямыми линиями. Так как это поверхности, бесконечно простирающиеся в направлении их образующих, то на изображениях их обычно ограничивают какими-либо линиями, например, следами этих поверхностей на плоскостях проекций или какой-либо из параллелей.

Если ось цилиндрической поверхности перпендикулярна какой-либо плоскости проекций, то поверхность называется проецирующей. Такая поверхность обладает свойством – все ее точки на соответствующей проекции отображаются на ее следе (окружности).

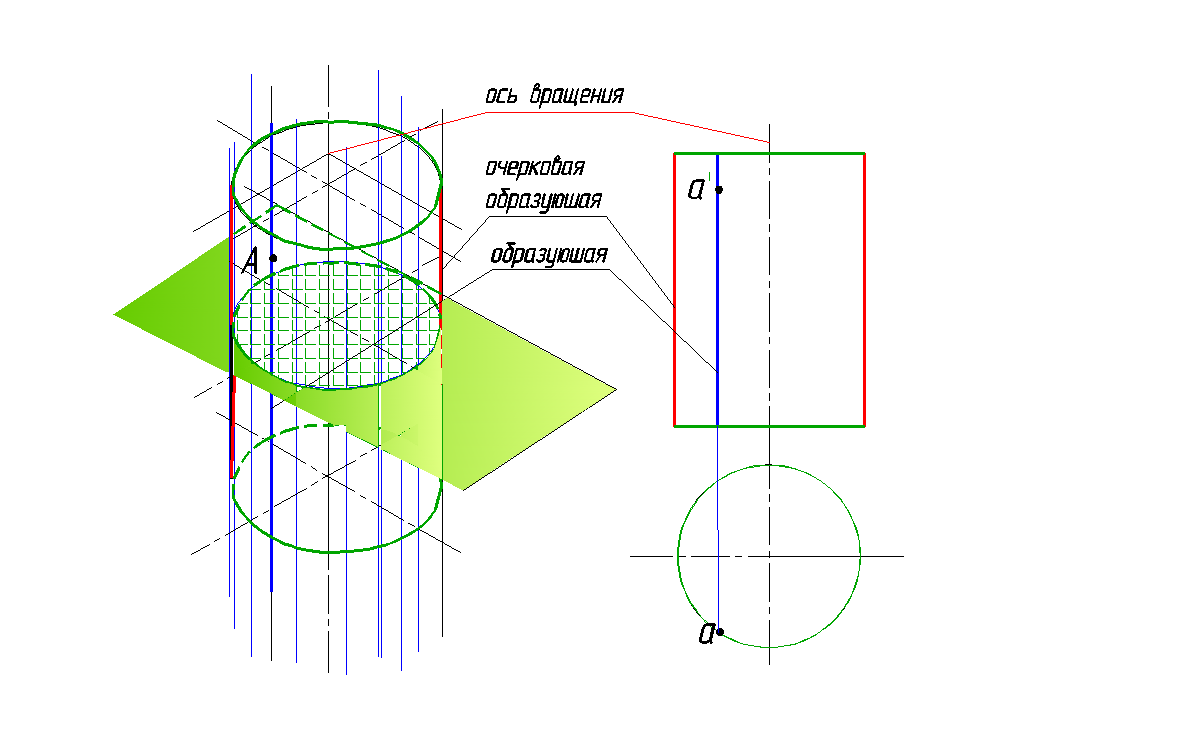
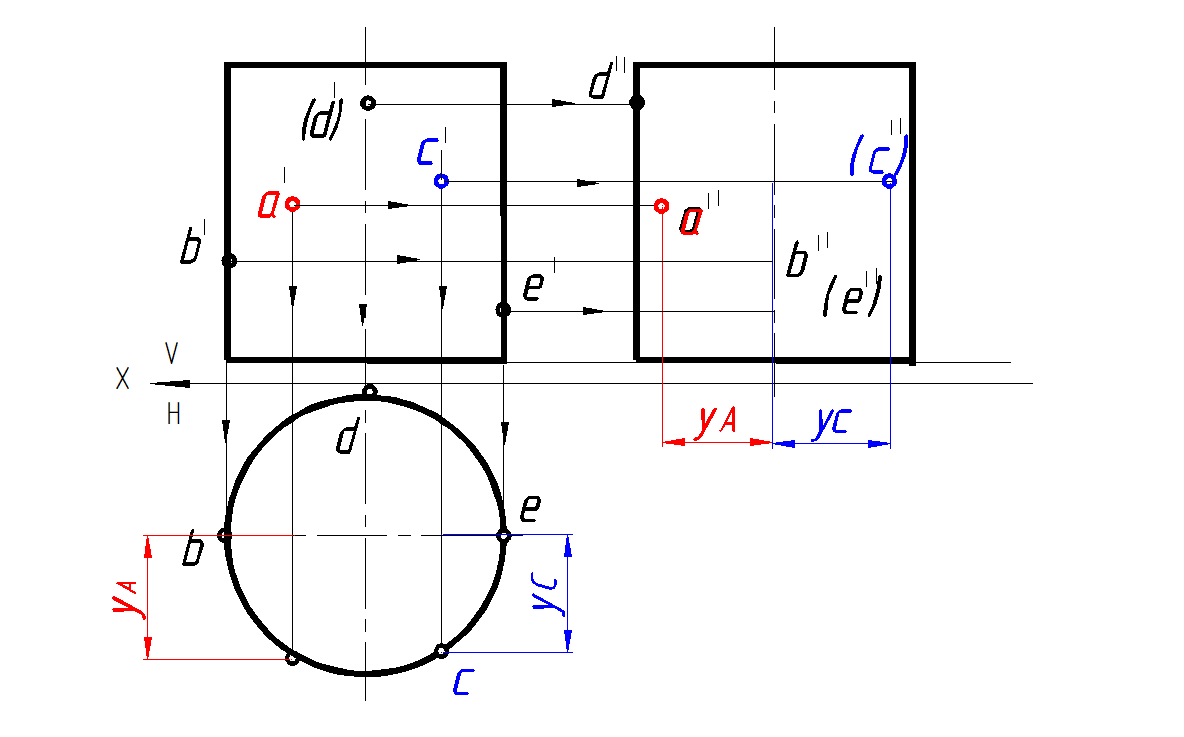
Рис. 145. Цилиндр вращения

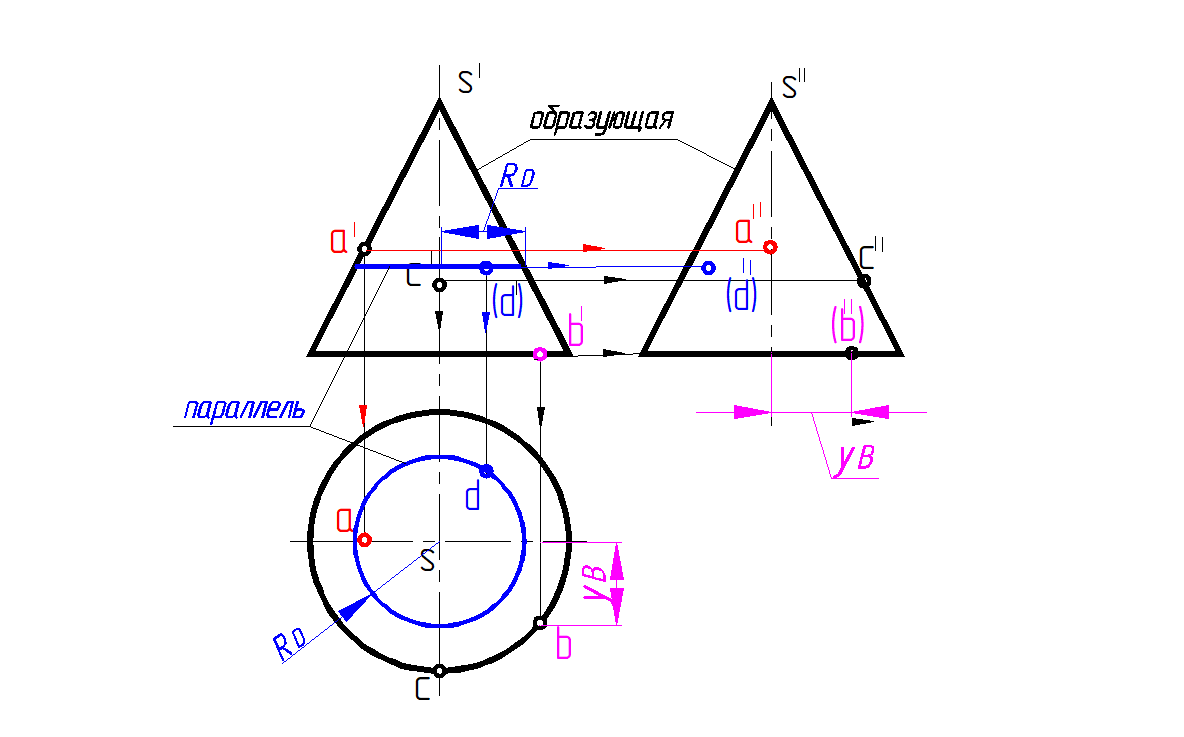
Рис. 146. Конус вращения

8. обобщенные позиционные задачи

ОСНОВНЫЕ ПОНЯТИЯ ОБ ОБОБЩЕННЫХ ПОЗИЦИОННЫХ ЗАДАЧАХ

Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности) геометрическим фигурам.

Позиционные задачи занимают важное место в начертательной геометрии. Ранее мы рассматривали такие задачи, связанные с нахождением точки пересечения прямой линии с плоскостью и построением линии пересечения плоскостей. Теперь рассмотрим способы решения позиционных задач с участием кривых линий и поверхностей. Эти задачи называют обобщенными. Задачи с участием прямых линий и плоскостей являются их частными случаями. В общем же случае эти задачи формулируют так:

Построить точки пересечения:

1) плоскости с поверхностью

2) линии с поверхностью

3) поверхности с поверхностью