Эти поверхности разделяются на три вида: цилиндрические, конические и поверхности с ребром возврата (торсы).
Цилиндрические поверхности образуются в том случае, когда все образующие пересекаются в несобственной точке (параллельны между собой и заданному направлению MN), а направляющая – произвольная кривая линия l (рис. 129, а). Определитель цилиндрической поверхности:
(a , l , MN); [a ∩ l , a || MN].
Геометрическая часть определителя – образующая прямая а, направляющая кривая l, прямая MN; алгоритмическая часть – любая образующая a пересекает направляющую l и проходит параллельно заданному направлению MN.
а б
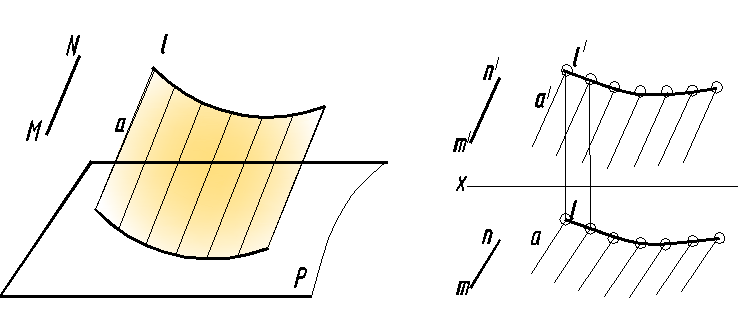
Рис. 129. Цилиндрическая поверхность
Цилиндрические поверхности различают по виду нормального сечения, т. е. кривой линии, получаемой при пересечении этой поверхности плоскостью, перпендикулярной к ее образующим.
Выделим случаи, когда нормальное сечение цилиндрической поверхности представляет собой кривую второго порядка. Такая цилиндрическая поверхность относится к числу поверхностей второго порядка. Точки любой поверхности второго порядка удовлетворяют в декартовых пространственных координатах уравнению второй степени. Любая плоскость пересекает такую поверхность по кривой второго порядка. Прямая линия пересекает поверхность второго порядка всегда в двух точках.
По виду нормального сечения цилиндр второго порядка может быть эллиптическим (в частном случае круговым), параболическим, гиперболическим. У известного из стереометрии прямого кругового цилиндра боковая поверхность является поверхностью второго порядка.
Если же нормальным сечением является неопределенная геометрическая линия, то это цилиндр общего вида.
Конические поверхности образуются, когда все прямолинейные образующие пересекаются в одной точке (собственной) S, а направляющая – кривая линия m (рис. 130). Определитель:
(a , m , S); [ai ∩ m , S є ai]
Геометрическая часть определителя: образующая прямая а, направляющая кривая m, точка S; алгоритмическая часть – любая образующая а i пересекает направляющую m и проходит через точку S.
а б
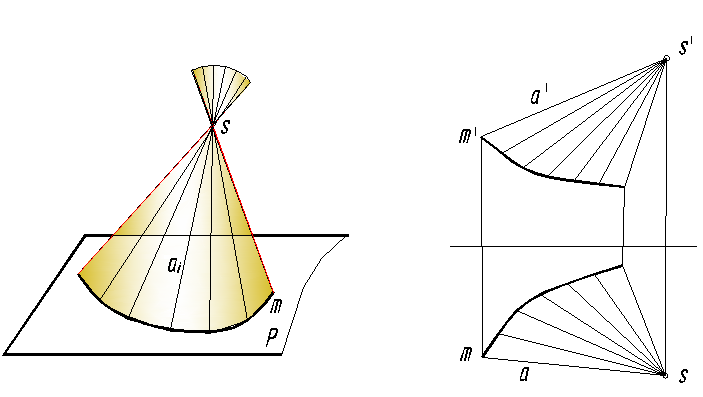
Рис. 130. Коническая поверхность
Цилиндрические и конические поверхности могут пересекать плоскость проекций; получается линия, называемая следом поверхности на данной плоскости проекций.
Цилиндрическая поверхность может быть задана ее следом на плоскости проекций и направлением образующей, коническая поверхность – следом на плоскости проекций и вершиной. Задаваясь точкой на следе, можно построить соответствующую образующую поверхности.
а б

Рис. 130. Цилиндрическая поверхность
Чтобы построить очерк цилиндрической или конической поверхности, нужно на каждой плоскости проекций отметить «граничные образующие», заключающие между собой область, внутри которой находится проекция поверхности. На следе цилиндрической поверхности отмечены те точки, через которые проходят проекции граничных образующих: А и В для фронтальной, С и D для горизонтальной проекции (рис. 130, а). Этими границами, а также линиями обрыва определяются контуры проекций поверхности, и производится разграничение видимой и невидимой частей поверхности на проекциях. Аналогичное построение выполнено для конической поверхности (рис. 130, б). Здесь обе проекции образующей SB оказались граничными: одна для фронтальной; другая для горизонтальной проекции конуса.
Точки на цилиндрических и конических поверхностях могут быть построены при помощи проходящих через них образующих. На рис. 131, а показано построение горизонтальной проекции точки Е, принадлежащей цилиндрической поверхности и заданной фронтальной проекцией. На рис. 131, б дан пример построения фронтальной проекции точки F, принадлежащей конической поверхности и заданной горизонтальной проекцией. В обоих случаях построение выполнено при помощи соответствующей образующей.
а б
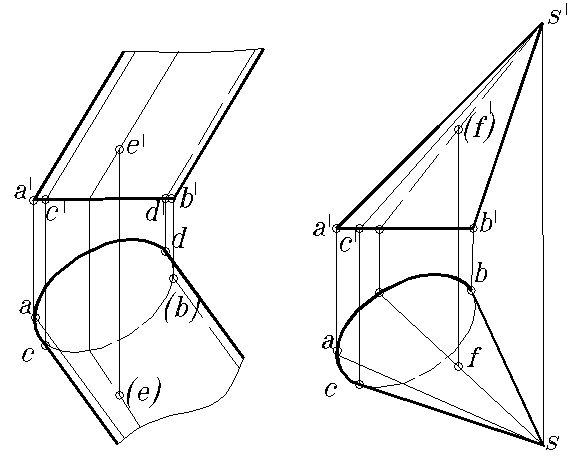
Рис. 131. Построение очерков цилиндрической (а) и конической (б) поверхностей
Нелинейчатые поверхности
Эти поверхности могут быть с образующей переменного или постоянного вида. Широкое применение в инженерной практике получили нелинейчатые поверхности с переменной образующей – каналовые и циклические.
Каналовой называют поверхность, образованную непрерывным перемещением замкнутых плоских сечений (не окружностей) по криволинейной направляющей. Площади этих сечений могут оставаться постоянными или монотонно изменяться в процессе перехода от одного сечения к другому. Чаще эти сечения (P1, P2…) параллельны некоторой плоскости или перпендикулярны к направляющей линии m (рис. 132, а).
Циклические поверхности образуются с помощью окружности, центр которой перемещается по криволинейной направляющей. В процессе движения радиус окружности монотонно меняется (рис. 132, б).
Циклическую поверхность можно рассматривать как частный случай каналовой поверхности.
Частным же случаем циклической поверхности является трубчатая поверхность. Здесь образующая – окружность – остается постоянной в процессе перемещения по криволинейной направляющей; плоскость окружности все время остается перпендикулярной к направляющей. Следовательно, трубчатую поверхность можно отнести и к классу поверхностей с постоянной образующей.
а б
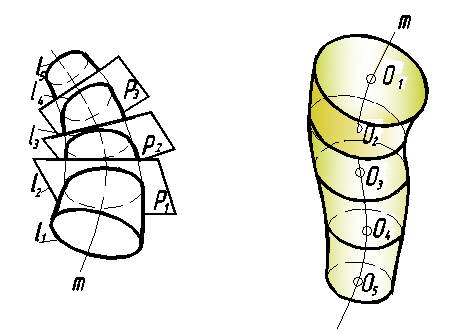
Рис. 132. Нелинейчатые поверхности с переменной образующей:
а – каналовые; б – циклические
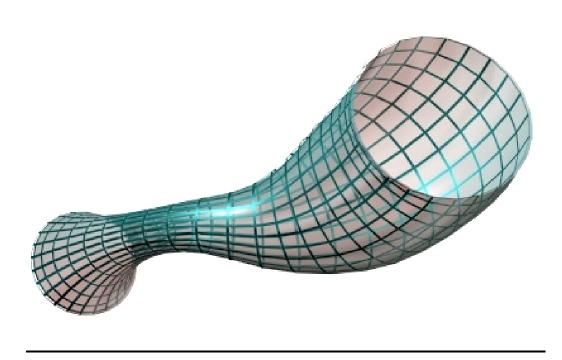

Рис. 133. Нелинейчатые поверхности с переменной образующей:
а – циклическая ; б – трубчатая
Винтовые поверхности
Поверхность называется винтовой, если она получается винтовым перемещением образующей. В зависимости от формы образующей винтовые поверхности могут быть линейчатыми и нелинейчатыми. Определитель этой поверхности имеет вид:
(a , m) ; [A].
Геометрическая часть определителя – образующая a, направляющая винтовая линия m; алгоритмическая часть – А – дополнительные указания о характере винтового перемещения образующей а.

Рис. 134. Винтовая поверхность
Наибольшее применение имеют винтовые поверхности с прямолинейной образующей и направляющей – винтовой линией постоянного шага. Такие поверхности называют геликоидами. Их характерной особенностью является постоянство угла наклона прямолинейной образующей к направляющей плоскости, за которую принята плоскость, перпендикулярная оси винтовой поверхности. В зависимости от величины этого угла геликоиды называют прямыми (угол равен 90°) и косыми или наклонным (угол произвольный – отличный от 0 и 90°). Чертеж прямой винтовой поверхности приведен на рис. 135, а. По своему образованию эта поверхность является коноидом, т. к. образующая АВ – прямая линия; она во всех положениях параллельна некоторой плоскости (в данном случае перпендикулярной оси винтовой линии); образующая пересекает две направляющие линии, кривую и прямую (ось) и движется вдоль оси вверх. Так как кривая направляющая представляет винтовую линию, то такой коноид называется винтовым или прямым геликоидом.
Изображение косой винтовой поверхности – косого геликоида – приведено на рис. 135, б. Проекции отрезка АО – образующей – изображены в ряде последовательных положений. Точка А перемещается по винтовой линии. Соответствующие положения проекций точки О отмечают на оси, руководствуясь тем, что проекция отрезка АО на ось вращения постоянна по величине (l).
а б
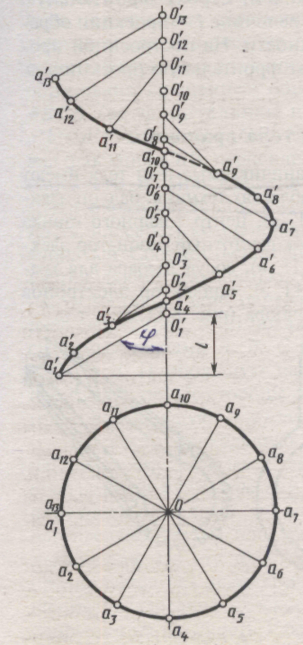
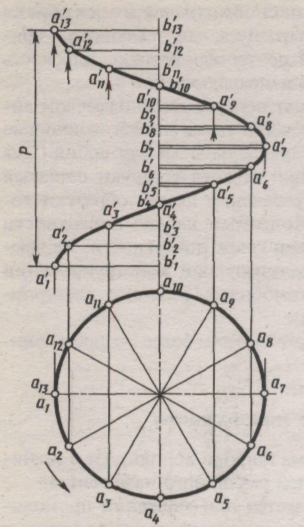
Рис. 135. Геликоид:
а – прямой; б – косой
Поверхности вращения
В числе кривых поверхностей – линейчатых и нелинейчатых – можно выделить обширный класс поверхностей вращения, объединенных одним законом образования. Это поверхности, получаемые при вращении какой-либо образующей (прямой, кривой, плоской или пространственной) вокруг неподвижной прямой – оси вращения.
Широкое применение поверхности вращения и ограничиваемые ими тела получили в технике, что объясняется распространенностью вращательного движения и простотой обработки их на станках. Типичными представителями этих поверхностей служат и гончарные изделия. Их образующие, как правило, плоские кривые линии. В состав определителя поверхности вращения входят: образующая m и ось вращения i (рис. 136, а). Каждая точка (А, В, С) образующей m при вращении вокруг оси i описывает окружность, называемую параллелью (рис. 136, б). Самую большую параллель называют экватором (на ней находится точка C), наименьшую (ее описывает точка В) – горлом.
Плоскости, проходящие через ось поверхности вращения, называются меридиональными, а линии, по которым они пересекают поверхность, меридианами. Меридиональную плоскость, параллельную плоскости проекций, называют главной меридиональной плоскостью Р (след РН), а линию пересечения ее с поверхностью вращения – главным меридианом.
Положение точки на поверхности вращения определяется при помощи параллели, проходящей через эту точку. Но это не исключает возможности применять прямолинейные образующие в случае линейчатых поверхностей вращения.
На рис. 136, б на экваторе показаны точка C. Границей видимости точек на фронтальной плоскости служит плоскость главного меридиана Р. С – граничная точка, находится на главном меридиане;
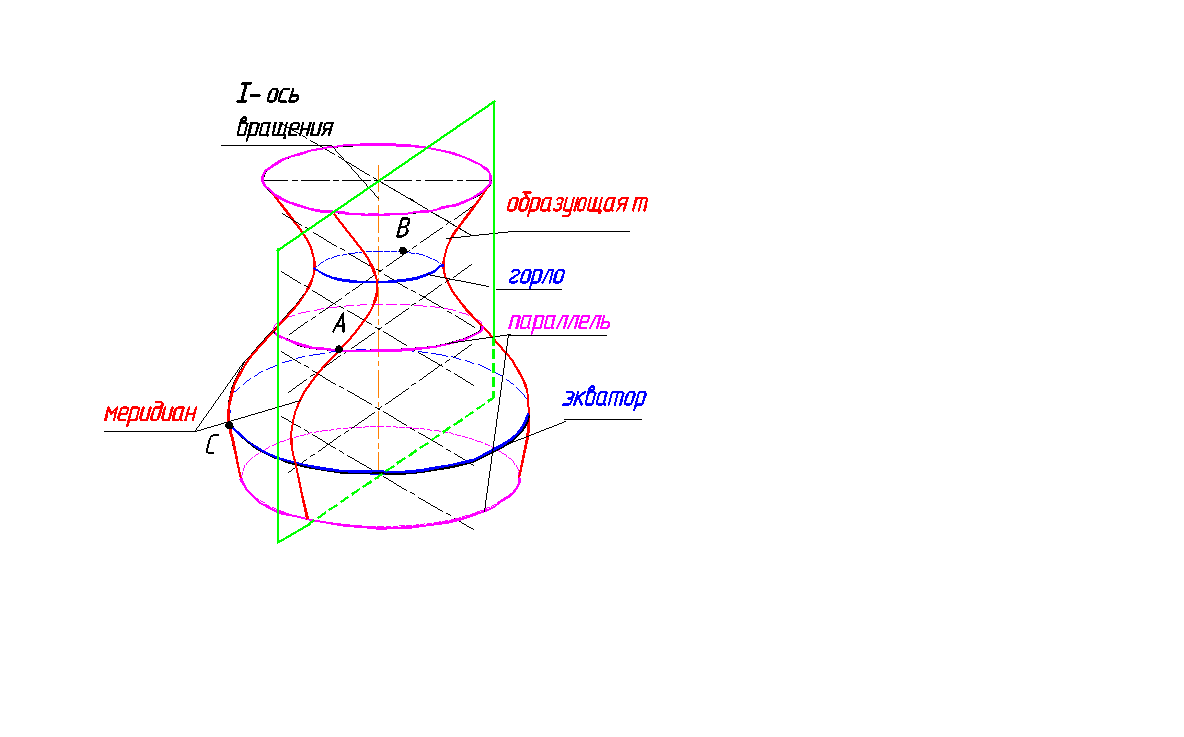
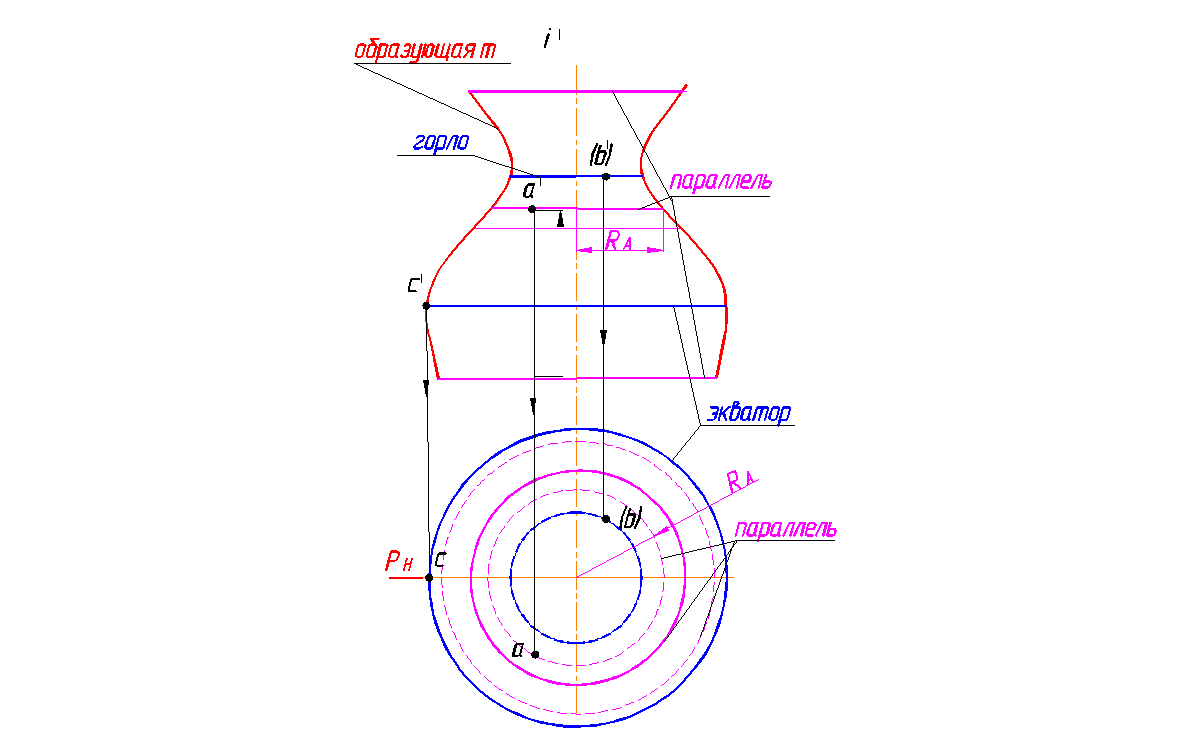
Рис. 136. Поверхность вращения
Наиболее удобными для выполнения изображений поверхностей вращения являются случаи, когда их оси перпендикулярны какой-либо плоскости проекций.
Наибольшее распространение получили поверхности вращения – алгебраические второго и четвертого порядка. Рассмотрим некоторые из них.
Тор – поверхность 4-го порядка, образованная вращением окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.
Разновидности тора: открытый или круговое кольцо (рис. 137, 138); самопересекающийся – окружность пересекает ось (рис. 139); закрытый – окружность касается оси (рис. 140); глобоид - образующей этой поверхности является дуга окружности, ось вращения которой располагается вне очерка окружности с наружной стороны (рис. 141).
Точки на поверхности тора, как и для всех поверхностей вращения, определяют по принадлежности их его параллелям. При этом надо иметь ввиду, что в плоскостях перпендикулярных оси тора, есть два семейства параллелей: линии пересечения плоскостей с наружной поверхностью (точки А и D лежат на такой параллели на рис. 138) и линии пересечения плоскостей с внутренней поверхностью тора (точки В и С).
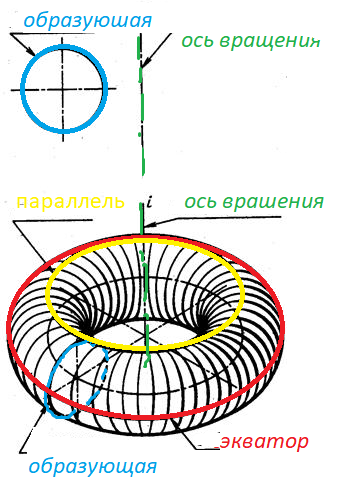
Рис. 137. Тор открытый – пространственная модель
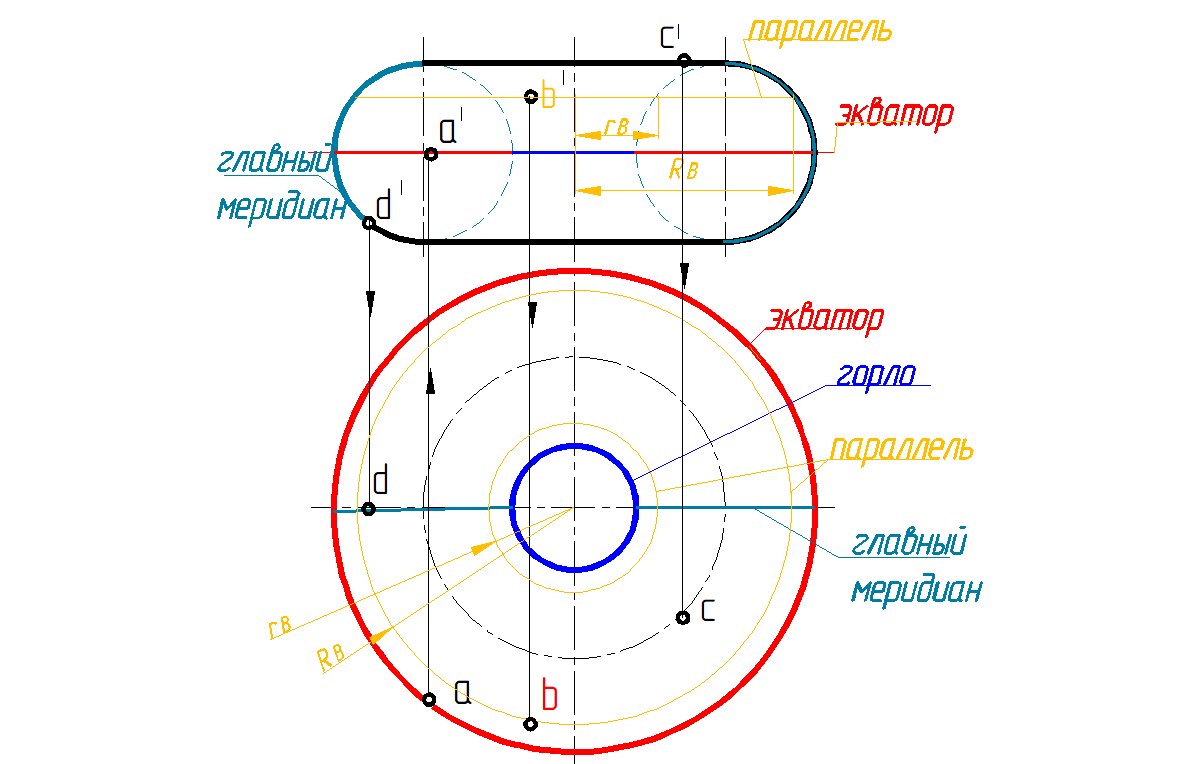
Рис. 138. Тор открытый на эпюре Монжа
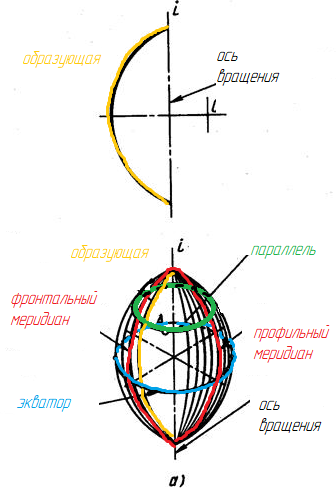
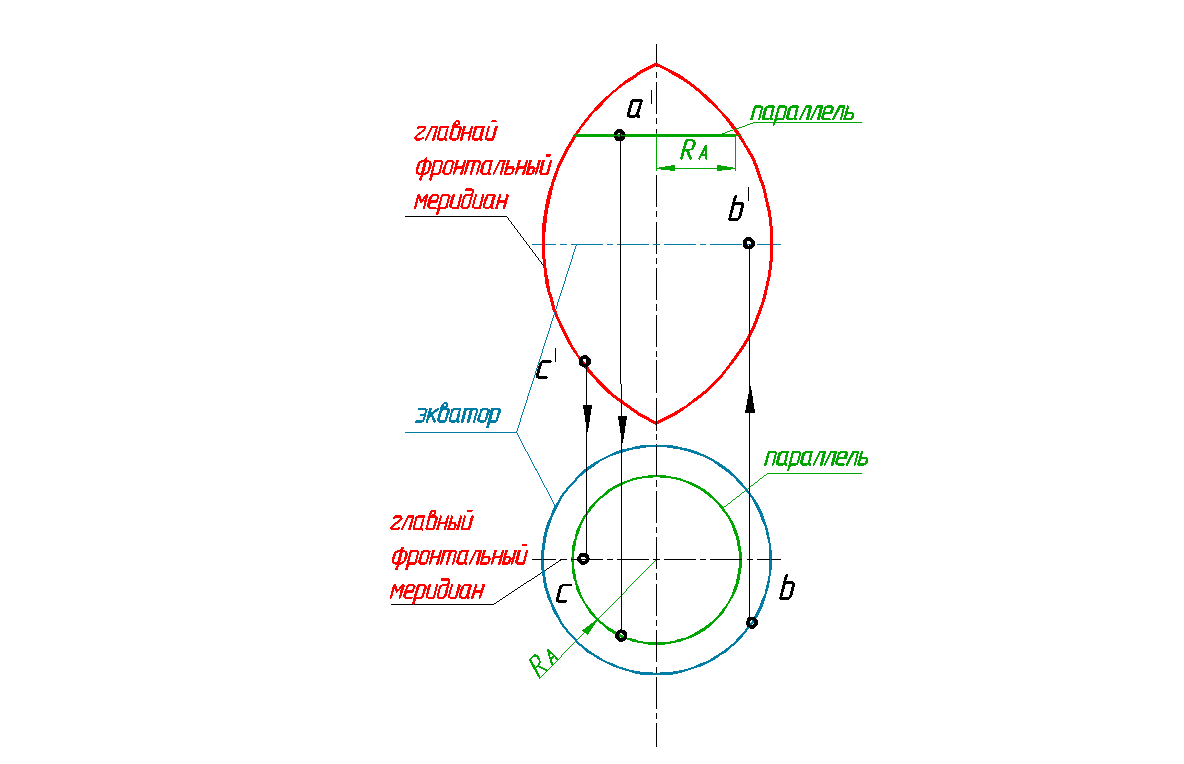
Рис. 139. Самопересекающийся тор
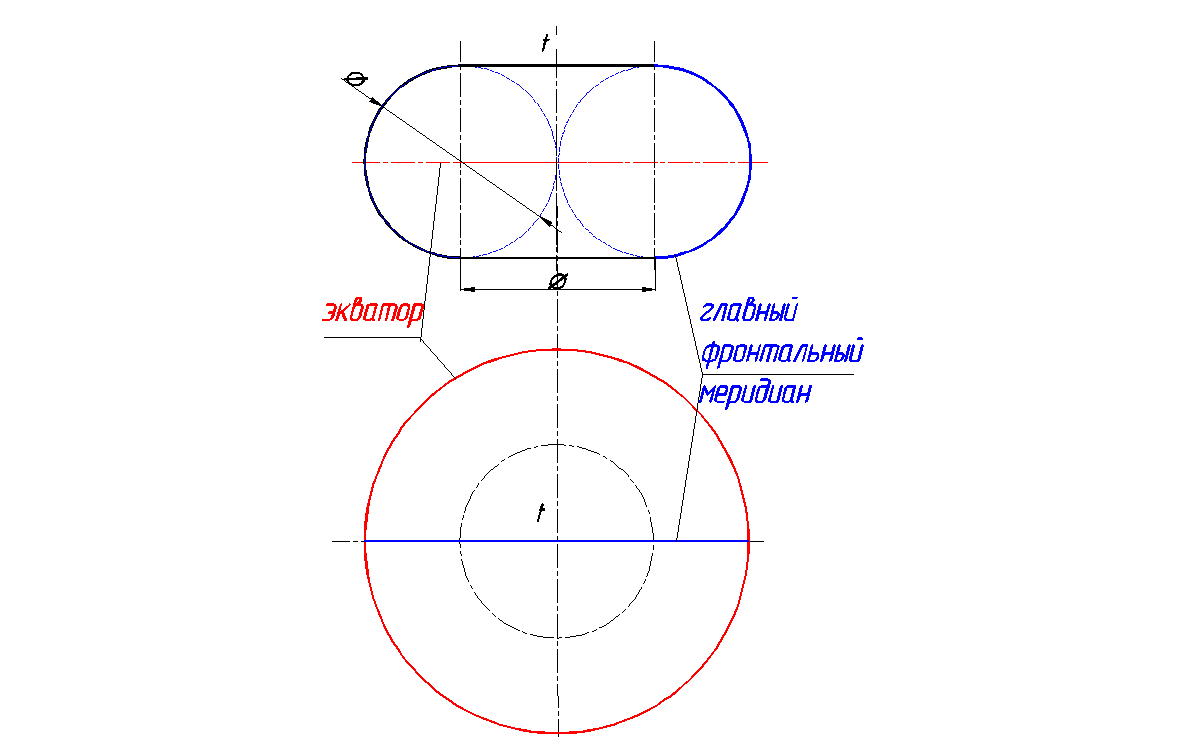
Рис. 140. Закрытый тор
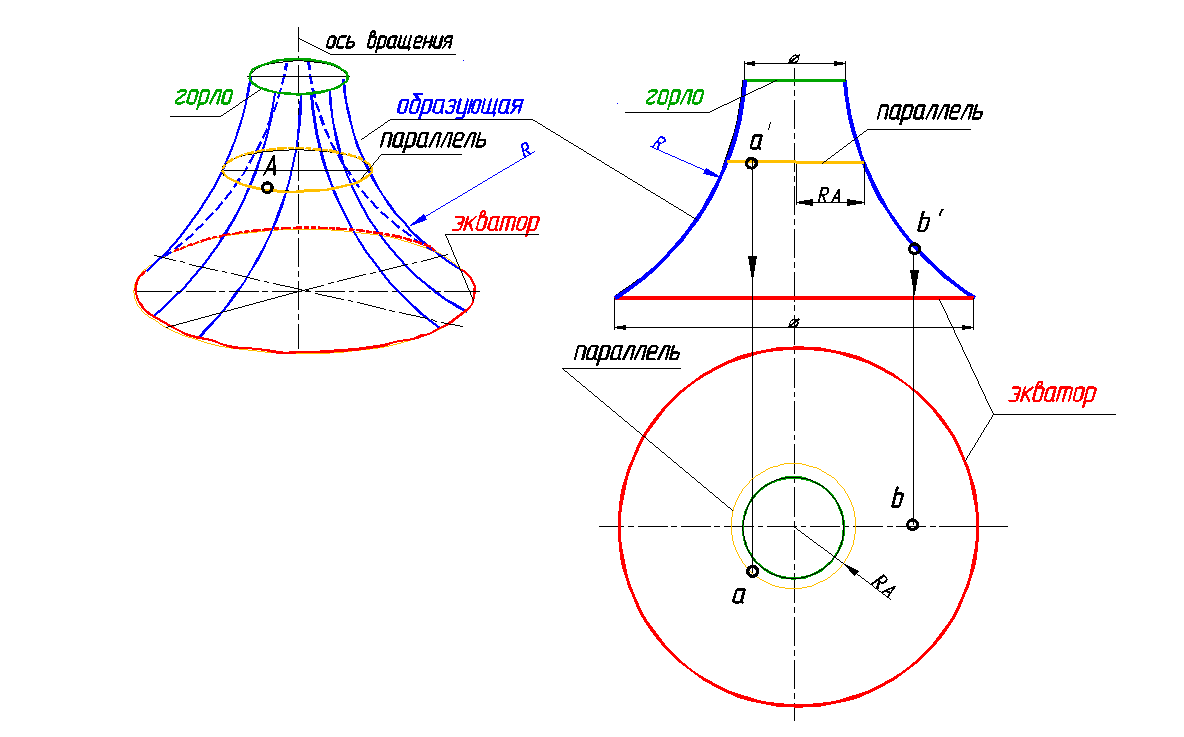
Рис. 141. Глобоид
Поверхности вращения 2-го порядка образуются вращением кривой 2-го порядка вокруг своей оси: сфера, эллипсоид, гиперболоид, параболоид.
Сфера
Сфера – поверхность, образующей которой является окружность с центром на оси вращения (рис. 142). Геометрическое тело, полученное вращением полукруга вокруг диаметра, который одновременно является осью вращения, называется шapом.
Каждая точка поверхности сферы удалена от ее центра на одинаковое расстояние. Если любую точку, принадлежащую поверхности, соединить с центром сферы, то этот отрезок будет радиусом сферы R.
Если через центр сферы прямой линией соединить две точки, принадлежащие поверхности, то этот отрезок будет диаметром сферы.
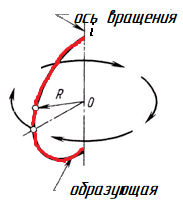
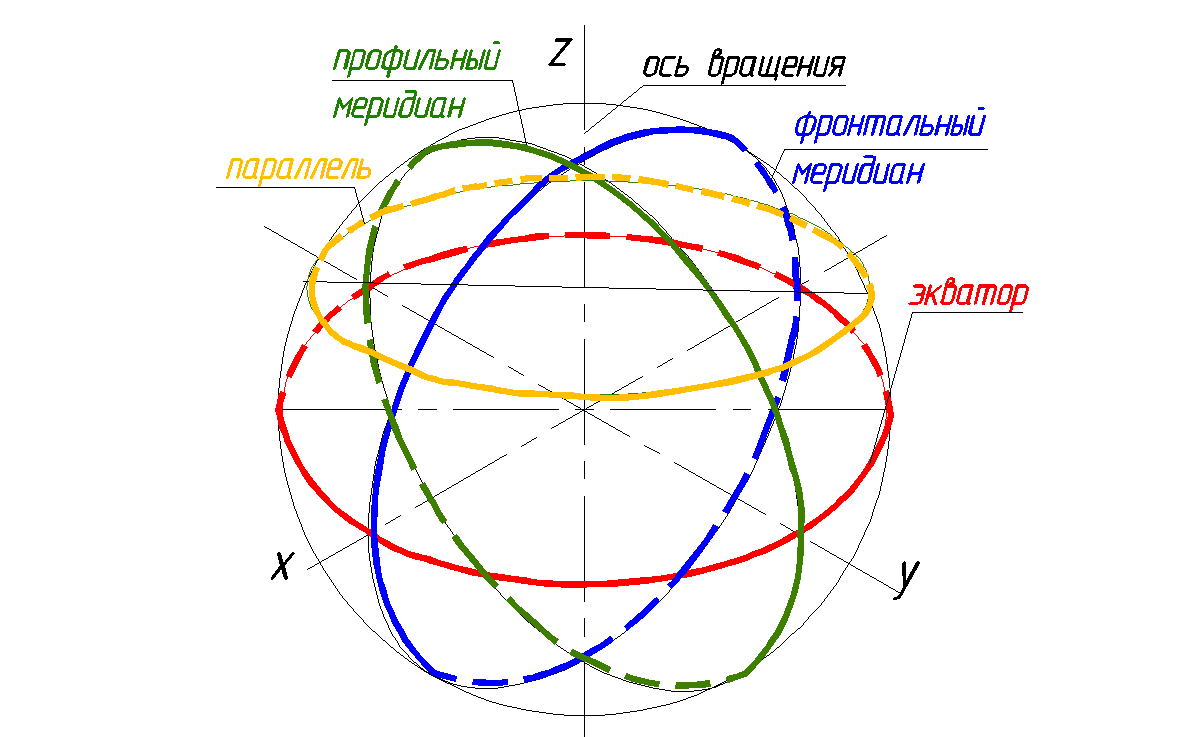
Рис. 142. Сфера
Дата: 2018-11-18, просмотров: 1549.