Поверхность прямого кругового конуса занимает особое место, т. к. служит носителем плоских кривых второго порядка – окружности, эллипса, параболы и гиперболы. Роль и область использования их в науке и технике огромна. Форма линии пересечения боковой поверхности прямого кругового конуса с плоскостью зависит от положения секущей плоскости и представляет собой:

1) две пересекающиеся прямые – образующие конуса (рис. 148а), если плоскость проходит через вершину конуса

2) окружность (рис. 148, б), если секущая плоскость перпендикулярна оси вращения конуса);

3) эллипс (рис. 148, в), если секущая плоскость не перпендикулярна к оси конуса и пересекает все его образующие;

4) параболу (рис. 148, г), если плоскость параллельна одной образующей конуса;

5) гиперболу (рис. 148, д), если плоскость параллельна оси конуса (или двум образующим)

                       а                                                   б

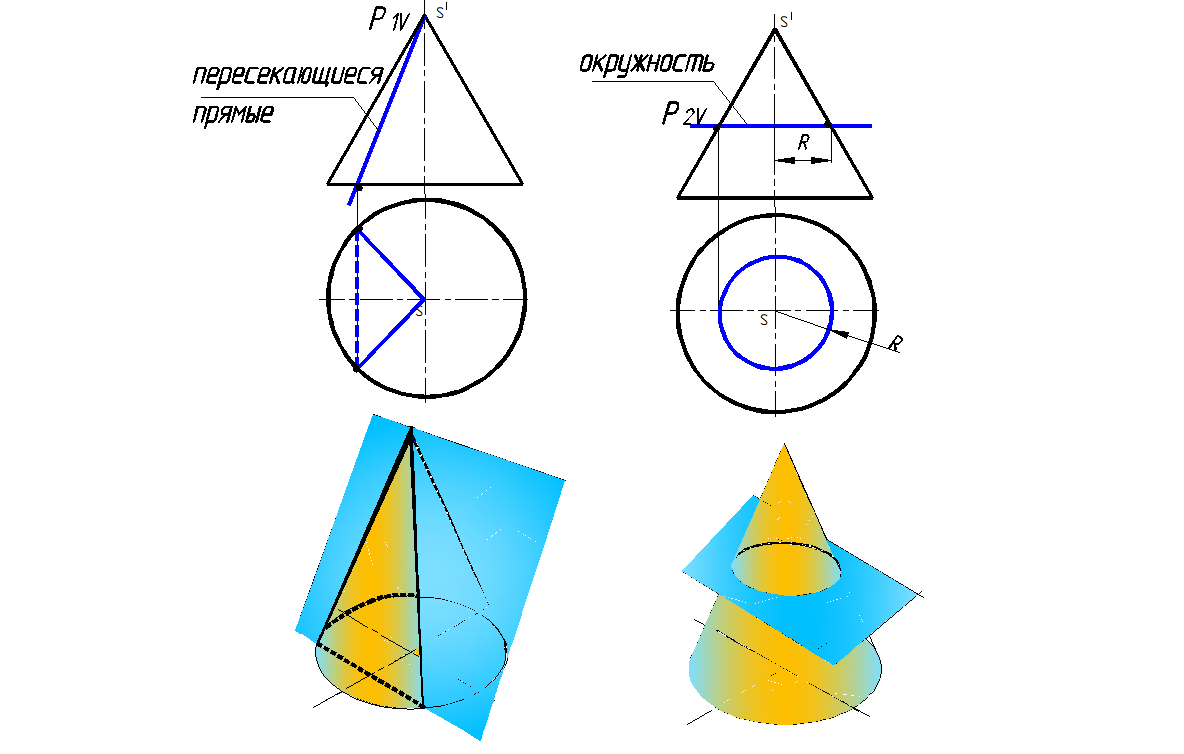
Рис.148. Конические сечения (окончание см. на с. 11)

            в                                      г                             д

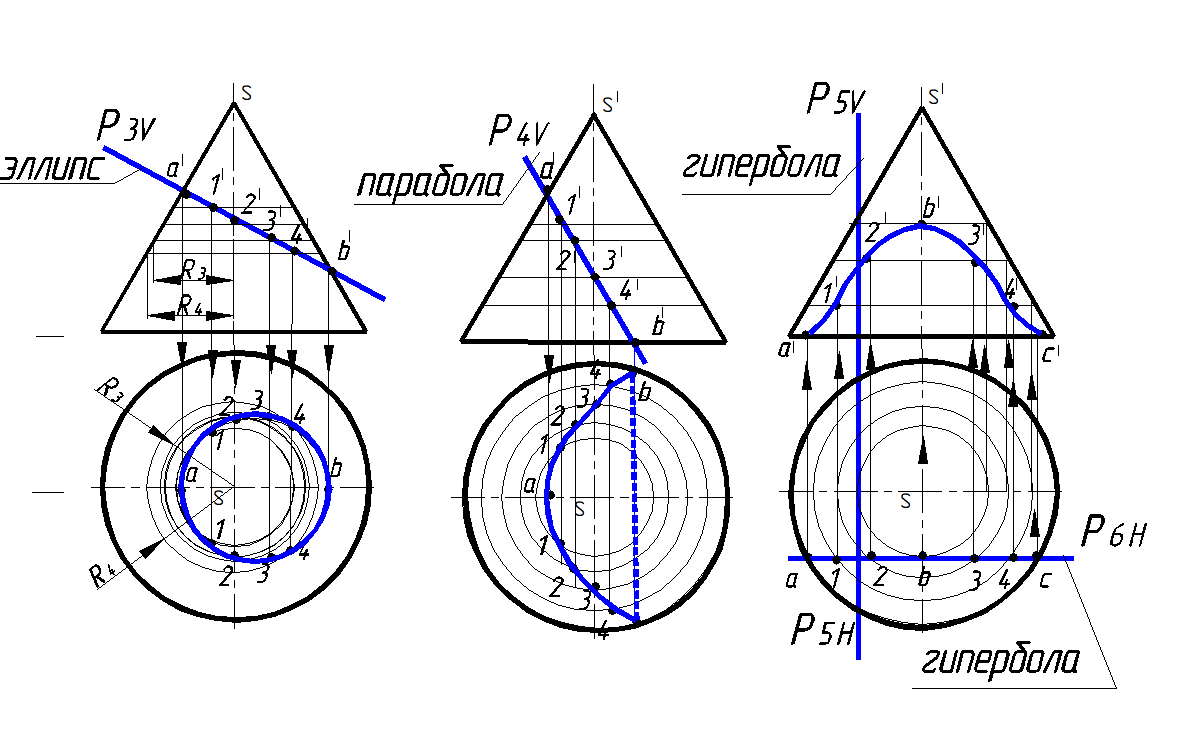
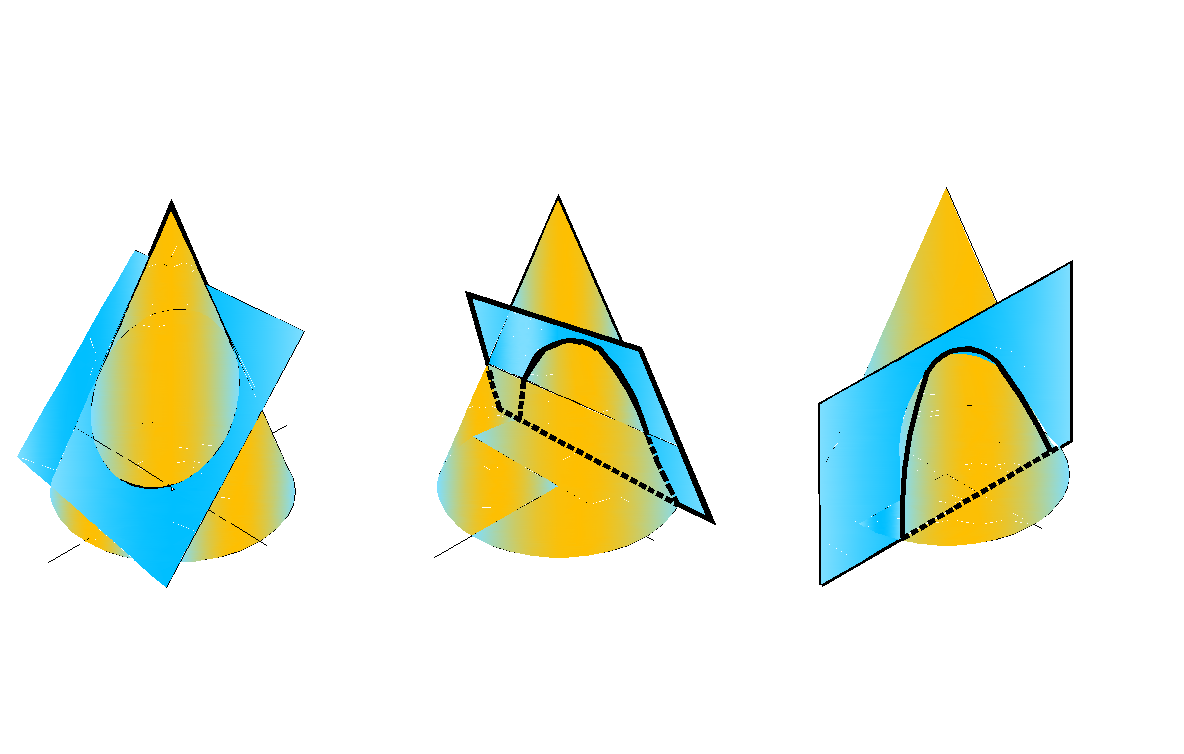
Рис.148. Окончание (начало на с. 10)

Пересечение сферы плоскостью

Как бы ни была направлена секущая плоскость, она всегда пересекает сферу по окружности, которая может проецироваться в виде отрезка прямой, в виде эллипса или окружности в зависимости от положения секущей плоскости.

Задача.

По заданной фронтальной проекции сферы с вырезом построить горизонтальную и профильную проекции (рис. 149).

Решение:

1.Анализ графического условия:

Вырез сферы выполнен плоскостями Р1 и Р2, которые пересекают сферу по окружности. Но эти плоскости перпендикулярными фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р1 пересекая сферу по окружности, отображается на горизонтальной и профильной проекции в виде эллипса Фронтально-проецирующая плоскость Р2 является еще и профильной плоскостью уровня, то есть параллельна профильной плоскости проекций. Поэтому отображается на профильной плоскости проекций без искажения – в виде окружности.

2.Строим характерные точки, лежащие на экваторе –точка В, главном фронтальном меридиане –точки А и Е и главном профильной меридиане- точка С.

3.Строим случайные точки, используя параллели сферы (например, точку N). Соединяем построенные точки, устанавливая при этом видимость линий.

4.Очерк сферы на горизонтальной проекции определяет линия экватора

от точки d до точки d и от точки b до точки b .

5.Очерк сферы на профильной проекции определяет линия главного профильного меридиана от точки с до точки с

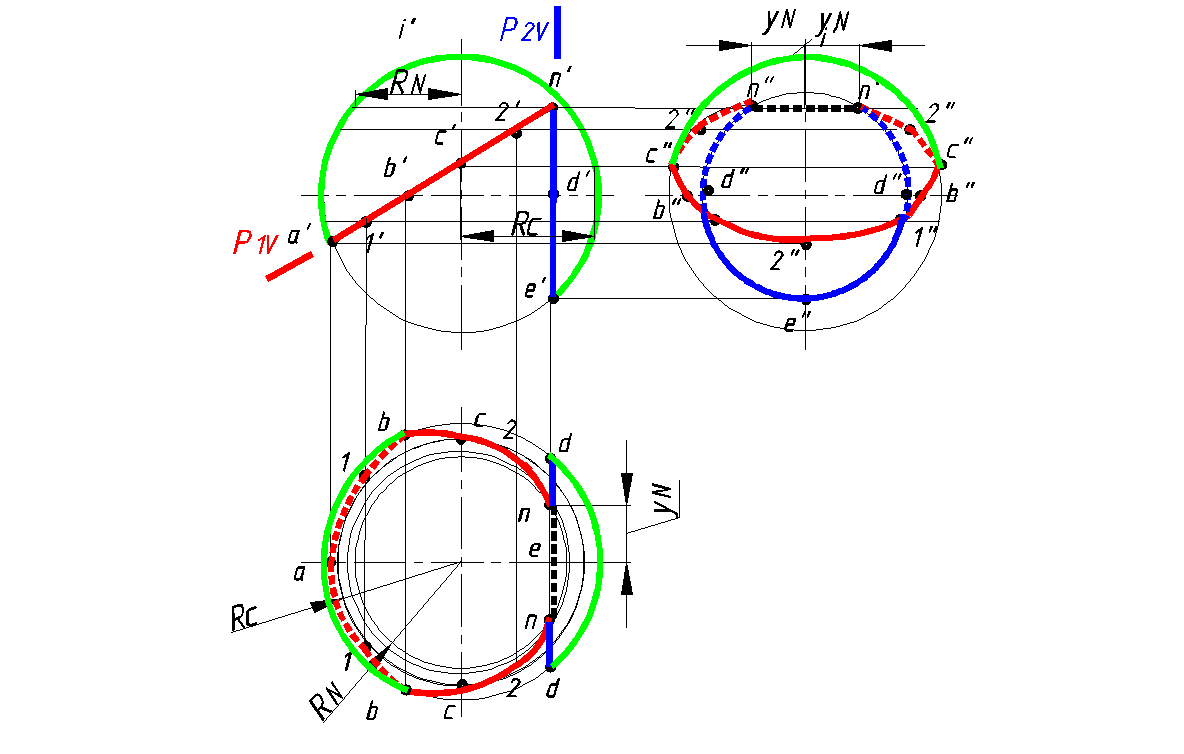
Рис. 149. Сфера с вырезом

 Пересечение тора плоскостью

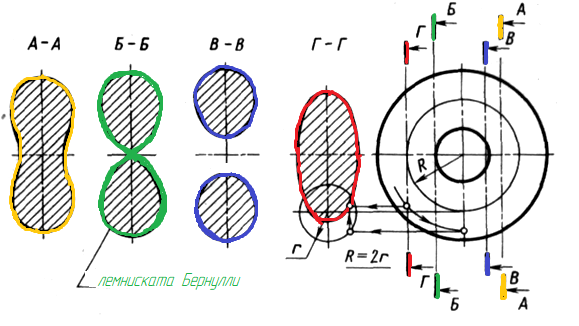
Тор- алгебраическая поверхность четвертого порядка. При пересечении тора плоскостью получаются плоские алгебраические кривые 4-го порядка, общее название которых – кривые Персея (в честь геометра Древней Греции). Вид кривых зависит от расстояния секущей плоскости до оси тора (рис. 150).

Кроме того, тор имеет три семейства окружностей:

Первое - секущие плоскости, проходят через ось тора. В сечении получаются две окружности – образующие тора (меридианы)

 Второе - секущие плоскости проходят перпендикулярно оси вращения. В сечении получаются две окружности – параллели.

 Третье –секущая плоскость качается двух окружностей главного меридиана смешанным образом. В сечении получаются две окружности –круги Вилларсо

Рис. 150. Сечения тора – кривые Персея

Задача.

По заданной фронтальной проекции тора с вырезом построить его горизонтальную проекцию (рис. 151).

Решение:

1.Анализ графического условия:

Вырез тора выполнен плоскостями Р 1 и Р 2. Плоскость Р1 пересекает тор по окружностям радиуса R A и R B .  Эта плоскость перпендикулярна фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р 1 пересекая тор по окружностям, отображается на горизонтальной в виде окружности, так как она является горизонтальной плоскостью уровня. Фронтально проецирующая плоскость Р 2 рассекает тор по кривой Персея, которая отображается на горизонтальной плоскости проекций с искажением

2.Строим характерные точки, лежащие на экваторе и на горле–точка D, главном фронтальном меридиане –точки А, В и N и главном профильной меридиане- точка С.

3.Строим случайные точки, используя параллели тора (например, точку 3). Соединяем построенные точки, устанавливая при этом видимость линий.

4. На горизонтальной проекции определяем очерк тора, оставшийся после выреза. Очерк тора на горизонтальной проекции определяется линией экватора. Линия экватора осталась после выреза от точки D с правой стороны оси вращения. Поэтому на горизонтальной проекции линия экватора определяется от точки d до точки d .

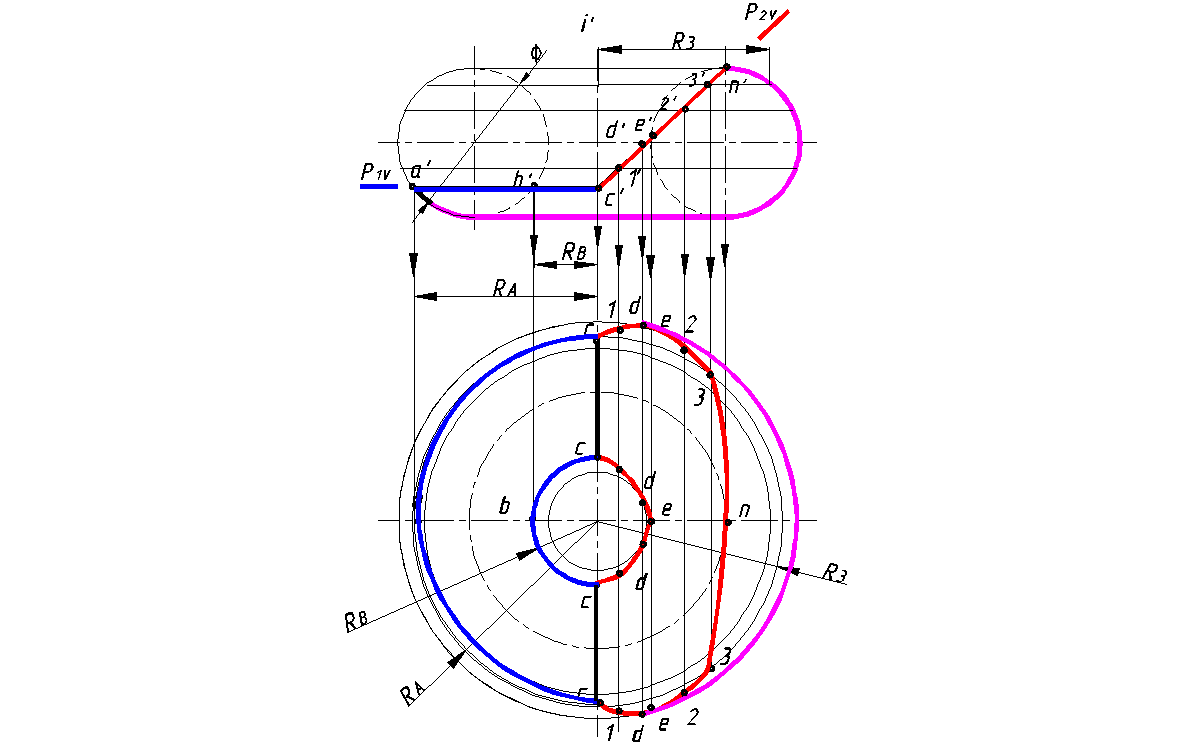
Рис. 151. Построение тора с вырезом