Суть преобразования плоскостей проекций:
1. Заданная геометрическая фигура не меняет своего положения в пространстве.
2. Вводится новая дополнительная плоскость перпендикулярно одной из основных плоскостей проекций. Таким образом возникает новая система плоскостей
3. Новая дополнительная плоскость проекций вводится так, чтобы эта же геометрическая фигура в новой системе плоскостей стала занимать частное положение.
4. Каждая новая система плоскостей должна представлять собой систему двух взаимно перпендикулярных плоскостей;
5. На новые плоскости геометрическая фигура проецируется ортогонально;
6.Расстояние от точки до незаменяемой плоскости сохраняется.
Рассмотрим на примере точки A, что происходит с её проекциями при перемене плоскостей проекции (рис. 95).
Вводим новую фронтальную плоскость проекции V1, перпендикулярно к горизонтальной плоскости проекции H. Плоскость V1 пересекается плоскость H по прямой X1, которая и будет новой осью проекций .
При этом Z А остается постоянной, т.е. |а′ a Х| =| A а| и |a ′1a х1|=|Aa|
Следовательно, |а′ a х| =|a ′1a х1| (рис. 23)
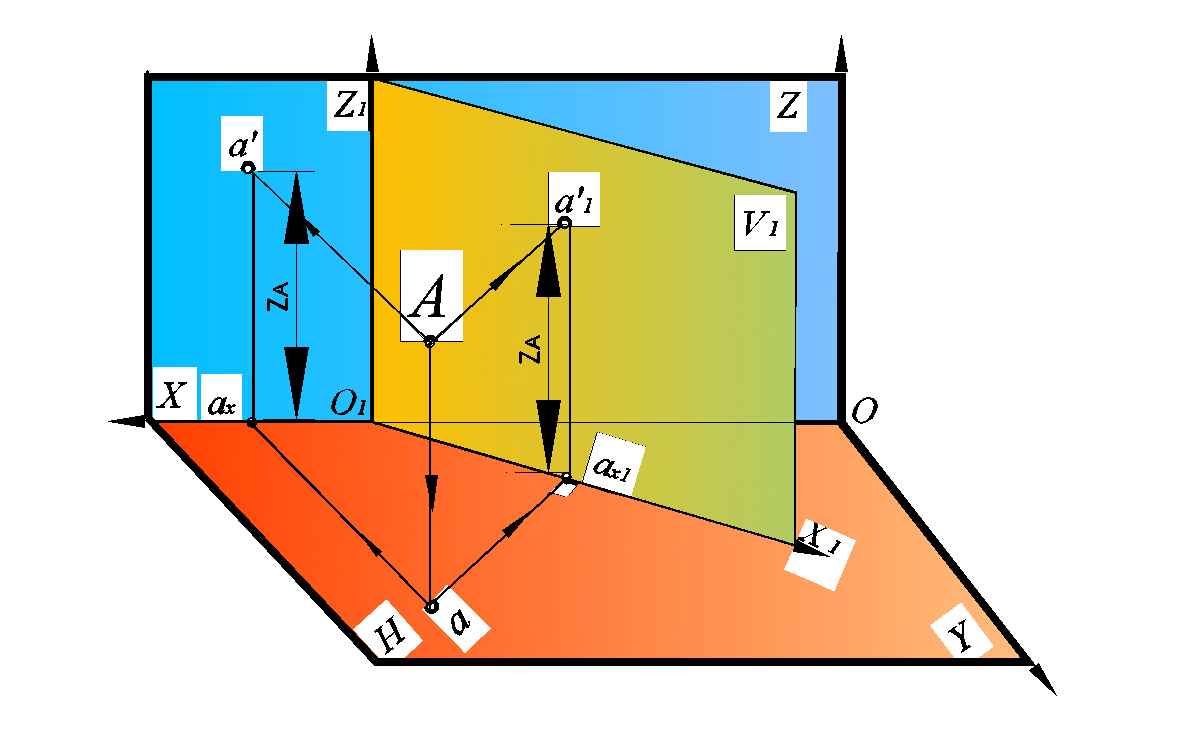
Рис. 95. Пространственная модель способа замены плоскостей точки А

Рис. 96. Чертеж способа замены плоскостей для точки А
Основные задачи по преобразованию комплексного чертежа
1. Преобразование отрезка прямой общего положения в отрезок прямой уровня.
Решение такой задачи позволяет не только найти натуральную величину отрезка прямой общего положения, но и определить угол наклона заданного отрезка прямой к основным плоскостям проекций в зависимости от конкретной поставленной задачи.
На рис. 97-98 показан отрезок прямой АВ, который в основной системе плоскостей V / H занимает общее положение.
В зависимости от того, какой угол наклона отрезка прямой, ∠ α или∠ β необходимо найти по условию задачи, решение может пойти двумя путями:
Определение угла наклона отрезка прямой АВ к горизонтальной плоскости проекций – ∠ α . Для определения угла α отрезка прямой необходимо преобразовать отрезок прямой АВ во фронтальную прямую уровня. Характерная проекция фронтальной прямой уровня является горизонтальная проекция. Она всегда параллельна оси ОХ. Следовательно, для преобразования отрезка прямой АВ во фронтальную прямую уровня, новую ось проекций ОХ1 проводим параллельно горизонтальной проекции прямой АВ.
Решение:
1. Вводим дополнительную плоскость проекций V1.
Условия ввода плоскости V1:
– перпендикулярно плоскости Н
– параллельно отрезку АВ
2. Порядок выполнения графической части задачи (рис. 97):
– на чертеже ось ОХ1 проводим параллельно горизонтальной проекции отрезка прямой АВ на любом расстоянии от нее.
– в новой системе плоскостей H / V1 из точек а и b проводим линии связи перпендикулярно новой оси ОХ1
– откладываем от оси ОХ1 аппликаты Z А и Z В на линиях связи одноименных точек.
– соединяем построенные точки а′1 и b ′1. Получаем новую фронтальную проекцию прямой АВ – |а′1 b ′1|
В результате преобразования отрезок прямой АВ стал фронтальной прямой уровня. Следовательно, на новой плоскости проекций V1 отрезок прямой АВ проецируется в натуральную величину и угол, образованный проекцией |а'1 b ′1| с осью ОХ1 равен углу наклона отрезка прямой АВ к горизонтальной плоскости проекций –∠ αАВ

Рис. 97. Построение ∠ βАВ отрезка АВ Рис.98. Построение ∠ αАВ отрезка АВ
Определение угла наклона отрезка прямой АВ к фронтальной плоскости проекций – ∠ β
Для определения угла β отрезка прямой общего положения необходимо преобразовать заданный отрезок прямой АВ в горизонтальную прямую уровня – горизонталь. Характерной проекцией горизонтали является фронтальная проекция, она всегда параллельна оси проекций. Следовательно, для преобразования отрезка прямой АВ в горизонталь, новую ось проекций ОХ1 проводим параллельно фронтальной проекции прямой АВ. (рис. 98)
Решение:
1. Вводим дополнительную плоскость проекций Н1.
Условия ввода:
– перпендикулярно плоскости V
– параллельно отрезку АВ
2. Порядок выполнения графической части задачи (рис. 98):
– на чертеже ось ОХ1 проводим параллельно фронтальной проекции отрезка прямой АВ на любом расстоянии от нее.
– в новой системе плоскостей V / H1 из точек а и b проводим линии связи перпендикулярно новой оси ОХ1
– откладываем от оси ОХ1 ординаты УА и УВ на линиях связи одноименных точек.
– соединяем построенные точки а1 и b1. Получаем новую горизонтальную проекцию прямой АВ – а1 b1.
В результате преобразования отрезок прямой АВ стал горизонтальной прямой уровня. Следовательно, на новой плоскости проекций Н1 отрезок прямой АВ проецируется в натуральную величину и угол, образованный проекций а1 b1 с осью ОХ1 равен углу наклона отрезка прямой АВ к фронтальной плоскости проекций – ∠ βАВ
2. Преобразование линии уровня в проецирующую прямую
Дано: прямая AB – горизонталь, AB || H .
Преобразовать комплексный чертеж так, чтобы прямая AB стала фронтально проецирующей прямой в новой системе плоскостей.
Вспомним чертеж проецирующей прямой (рис.26-27)
а) AB – горизонтально проецирующая прямая, АВ ⊥ H (рис. 99):
горизонтальная проекция - характерная (точка), а′ b ′`⊥ OX

Рис. 99. Отрезок АВ ⊥ H
б) AB – фронтально проецирующая прямая .AB⊥ V (рис. 100):
фронтальная проекция – характерная (точка), ab⊥ OX ,

Рис.100. Отрезок AB⊥ V
Преобразование горизонтали АВ во фронтально проецирующую прямую.
Решение :
1. Вводим новую плоскость проекции V 1 :
V 1⊥ H , V 1⊥ AB (рис. 101)

Рис.101.АВ- фронтально проецирующая прямая
2. Новая ось X 1 – горизонтальный след плоскости V 1. Ось X 1 проводим перпендикулярно а b на любом расстоянии от точки b. В новой системе плоскостей прямая AB стала фронтально проецирующей прямой.
Преобразование фронтали АВ в горизонтально проецирующую прямую.
Решение :
1. Вводим новую плоскость проекции Н1:
H 1 ⊥V , Н1⊥ AB (рис. 102)
2. Новая ось X 1 – фронтальный след плоскости Н1. Ось X 1 проводим перпендикулярно а′ b ′ на любом расстоянии от точки b ′. В новой системе плоскостей прямая AB стала горизонтально проецирующей прямой.

Рис. 102.АВ- горизонтально проецирующая прямая
Задача.
Дата: 2018-11-18, просмотров: 1095.