Решение:

   Для преобразования прямой общего положения в проецирующую прямую потребуется два этапа:

1. Прямая из общего положения преобразуется в прямую уровня

2. Прямая уровня преобразуется в проецирующую прямую

Прямая общего положения преобразована в горизонтально проецирующую прямую (рис. 103)

 Прямая общего положения преобразована во фронтально проецирующую прямую (рис. 104)

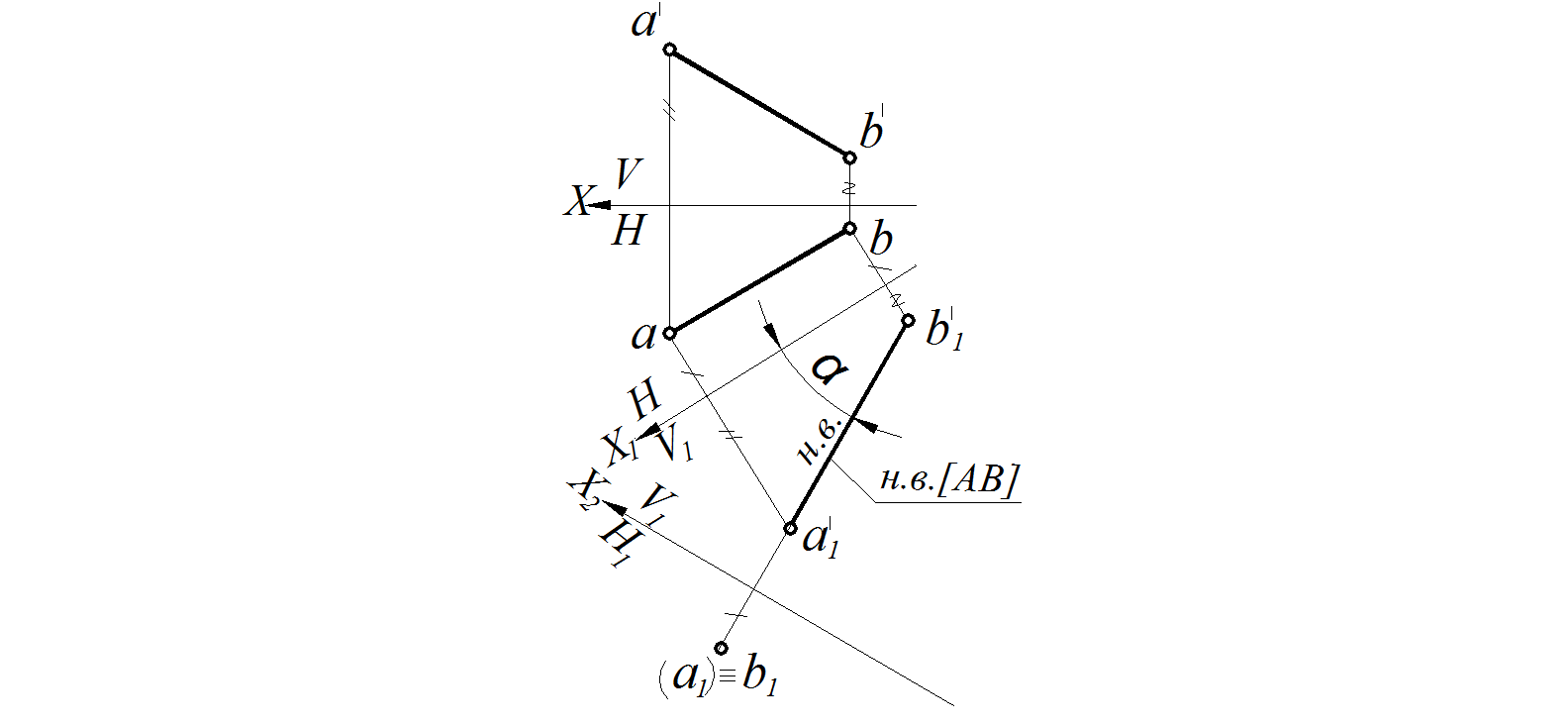
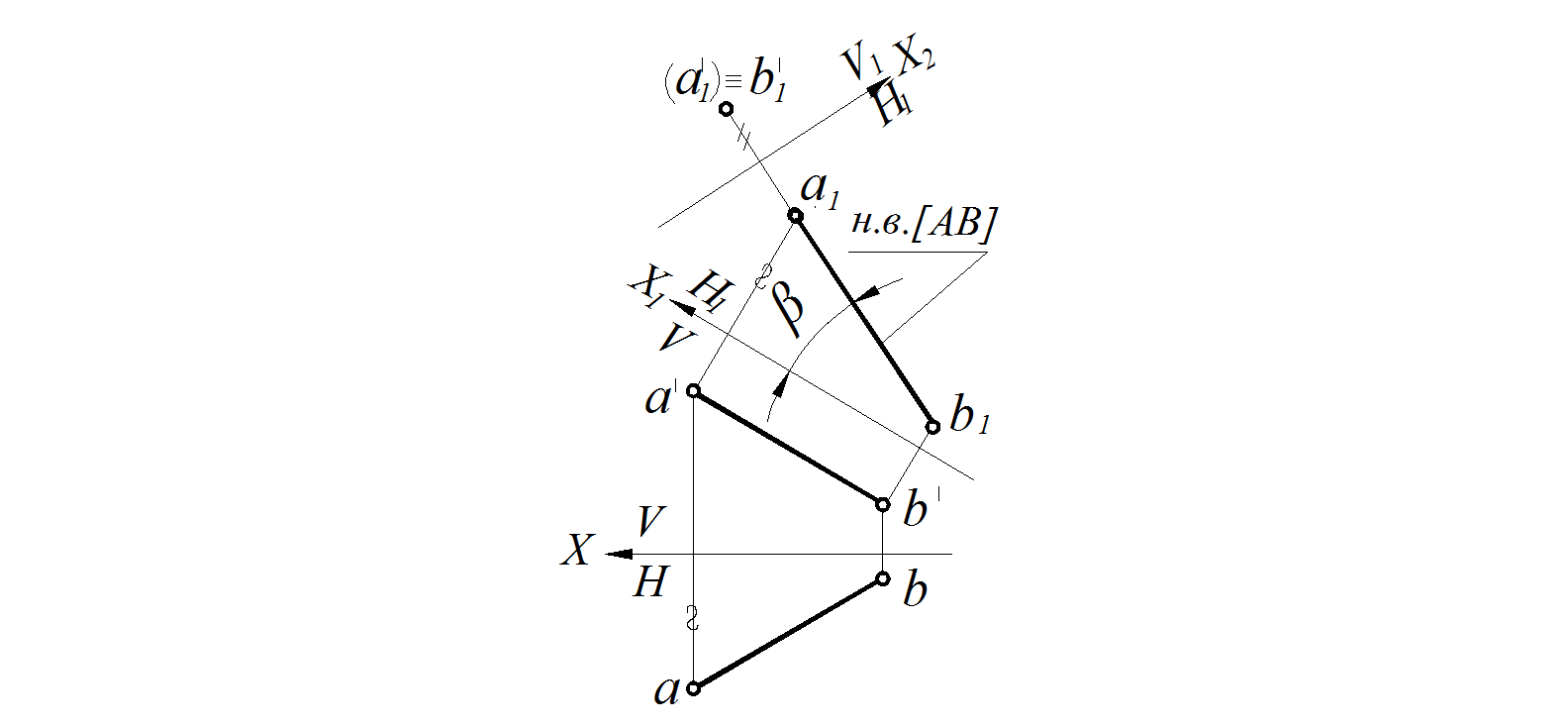
    Рис. 103. АВ ⊥ Н₁                                   Рис. 104. АВ ⊥ V₁

3. Преобразование плоскости общего положения в проецирующую плоскость (Определение углов наклона плоскости общего положения к плоскостям проекций)

Задача 1.

 Определить угла наклона плоскости общего положения к горизонтальной плоскости проекций-угла α

Решение

Анализируем графическое условие задачи: плоскость ΔABC – плоскость общего положения.

Для определения угла α заданной плоскости, необходимо преобразовать комплексный чертеж так, чтобы плоскость ΔABC стал фронтально проецирующей плоскостью в новой системе плоскостей.

Порядок выполнения графической части задачи:

1. Вводим новую плоскость проекции V₁: V₁ ⊥ H₁, V₁ ⊥ ΔABC.

2. Проводим в плоскости ΔABC горизонталь DC.

3. Ось проекции X₁ – горизонтальный след плоскости V₁ – проводим перпендикулярно прямой cd на любом расстоянии от точки d .

4. Проводим из точек a, b и d линии связи к новой оси X₁.

5. Откладываем от оси X₁ по линиям связи Z _С, Z _А, Z_В. Поскольку a ' принадлежит оси X, следовательно, a '₁ принадлежит OX₁.

   На новую плоскость проекций V₁ плоскость ΔABC отобразилась в впрямую линию, т. е. стала фронтально проецирующей плоскостью. На новой плоскости проекций V₁ угол наклона плоскости ΔABC к горизонтальной плоскости проекций α отображен без искажения (рис. 32).

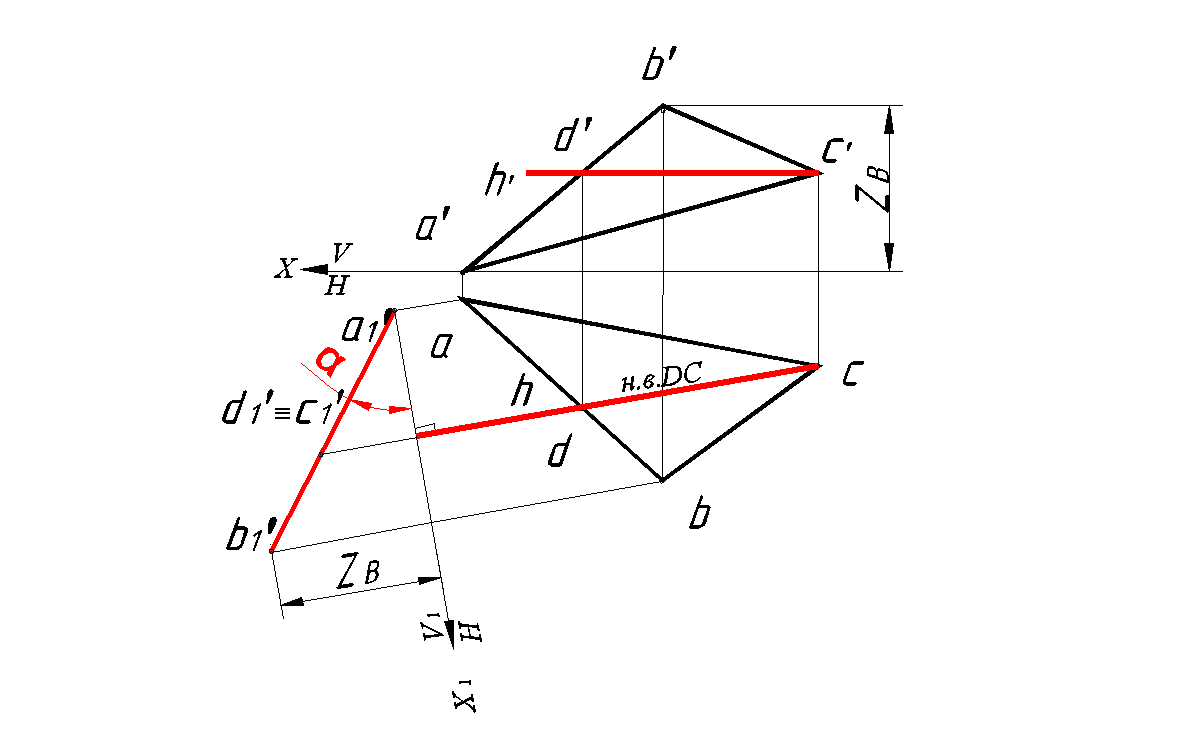
Рис. 105. Определение угла ∠α плоскости ∆АВС

Задача 2.

Определить угол наклона плоскости общего положения к фронтальной плоскости проекций – угол β

Решение:

Для определения угла β заданной плоскости необходимо преобразовать комплексный чертеж так, чтобы плоскость ΔABC стал горизонтально проецирующей плоскостью в новой системе плоскостей.

1. Вводим новую плоскость проекции Н₁: H₁ ⊥ V, Н₁ ⊥ ΔABC.

2. Проводим в плоскости ΔABC фронталь DC.

3. Ось проекции X₁ – фронтальный след плоскости Н₁, проводим перпендикулярно прямой c ′ d ′ на любом расстоянии от точки с ′.

4. Проводим из точек а ′,  b ′ , и d ′ линии связи к новой оси X₁.

5. Откладываем от оси X₁ по линиям связи У_С, У_А, У_В. Поскольку a ′ принадлежит оси X, a₁ принадлежит OX₁.

На новую плоскость проекций Н₁ плоскость ΔABC отобразилась в прямую линию, т. е. стала горизонтально проецирующей плоскостью. На новой плоскости проекций Н₁ угол наклона плоскости треугольника АВС к фронтальной плоскости проекций β отображен без искажения (рис. 106).

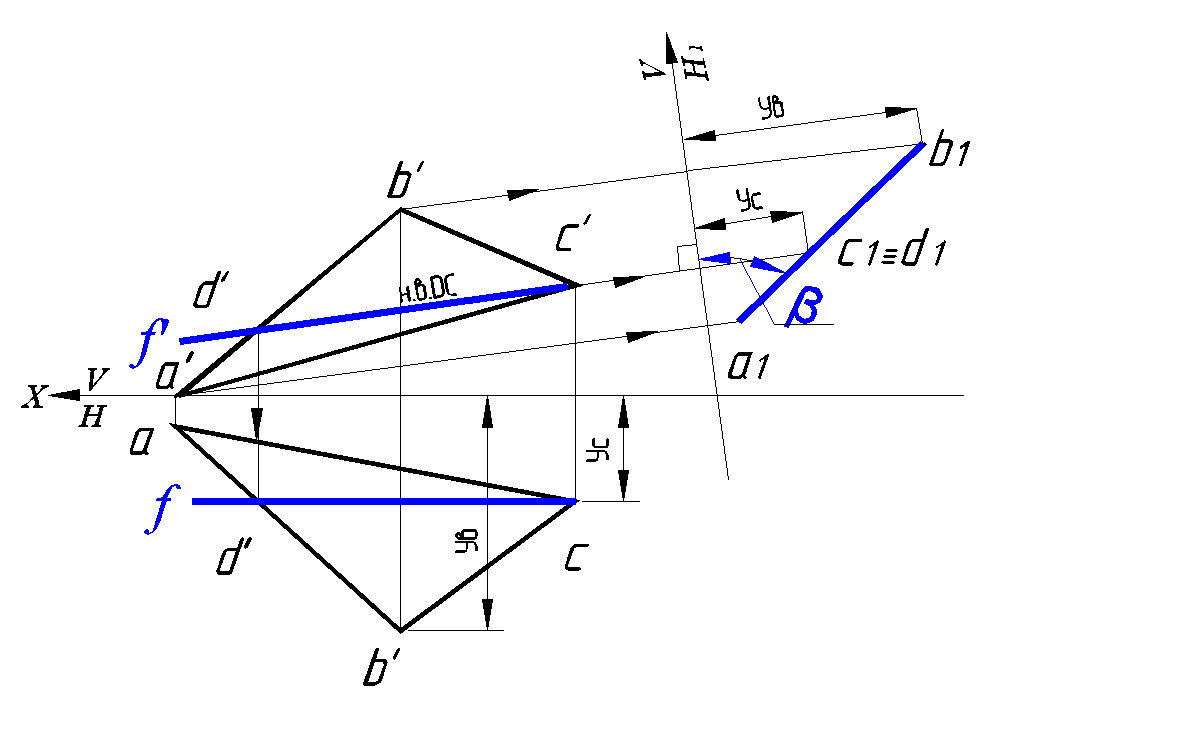
Рис. 106. Определение ∠β плоскости ∆АВС

4. Преобразование плоскости проецирующего положения в плоскость уровня (Определение натуральной величины плоской фигуры)

    Для определения натуральной величины плоской фигуры необходимо преобразовать комплексный чертеж так, чтобы проецирующая плоскость в новой системе плоскостей стала плоскостью уровня.

 Задача.

 Преобразовать комплексный чертеж так, чтобы плоскость Δ ABC стала фронтальной плоскостью уровня.

   Решение:

Анализируем графическое условие задачи: плоскость ΔABC – горизонтально проецирующая плоскость

1. Вводим новую плоскость проекции V₁. Условия ввода плоскости V₁: V₁ ⊥ H₁, V₁ ⊥ ΔABC .

2. Ось проекции X₁ – горизонтальный след плоскости V_1. Проводим ось X₁ параллельно горизонтальной проекции плоскости ΔABC на любом расстоянии от нее.

3. Проводим из точек a, b, и c линии связи (перпендикуляры к оси X₁).

4. Откладываем Z _С, Z _А, Z_В по линиям связи соответственно точкам A, B, C от оси X₁.

5. Получаем очки a₁′, b₁′, c₁′ . Соединяя полученные точки, получим новую проекцию плоскости ΔABC равную натуральной величине ΔABC .

 Следовательно, в новой системе плоскостей плоскость занимает положение фронтальной плоскости уровня (рис.107).

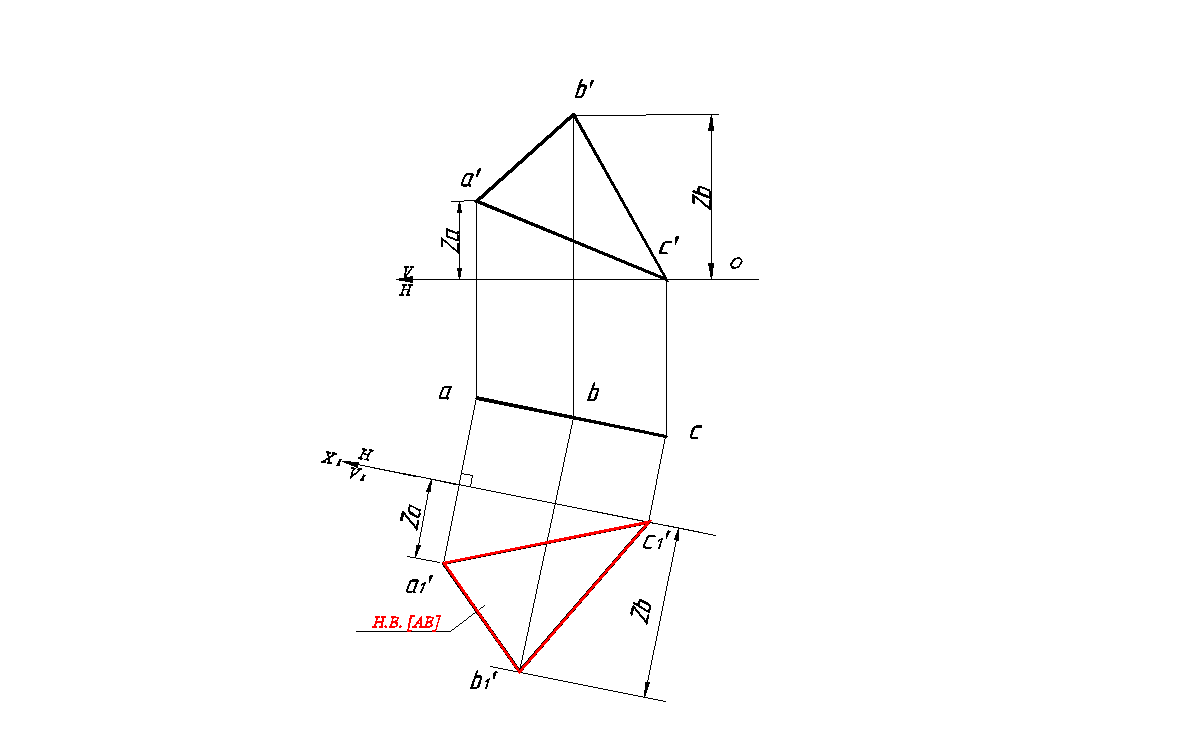
Рис. 107. Преобразование горизонтально проецирующей плоскости во фронтальную плоскость уровня

Задача.