(способ плоскопараллельного перемещения)

Геометрическая фигура перемещается в пространстве таким образом, что все ее точки двигаются в плоскостях, параллельных какой-либо плоскости проекций. При этом одна из проекций располагается в требуемое по ходу решения задачи положение, а другая проекция строится по правилам вращения – все точки этой проекции перемещаются по прямым, параллельным оси проекций. Например, для того чтобы перевести отрезок АВ прямой общего положения в проецирующее положение, необходимо последовательно выполнить два его перемещения (рис. 113). Сначала надо перевести его в положение, параллельное какой-либо плоскости проекций, например горизонтальной. Фронтальную проекцию, не меняющую своей величины, располагаем параллельно оси х:

а₁' b₁' = a ' b '; а₁' b₁' || x .

Горизонтальные проекции точек А и В перемещаются параллельно оси х и, построенная горизонтальная проекция а₁ b₁ выражает натуральную величину отрезка. Теперь можно отрезок перевести в положение перпендикулярное плоскости V. Располагаем проекцию а₂ b₂, равную а₁ b₁, перпендикулярно оси х:

а₂ b₂, = а₁ b₁; а₂ b_{2 ┴} х.

Фронтальная проекция выражается точкой.

Выполненные операции перемещения отрезка АВ можно представить и как вращение, но положение осей не указано. Их можно найти, но, как видно, необходимости в этом нет.

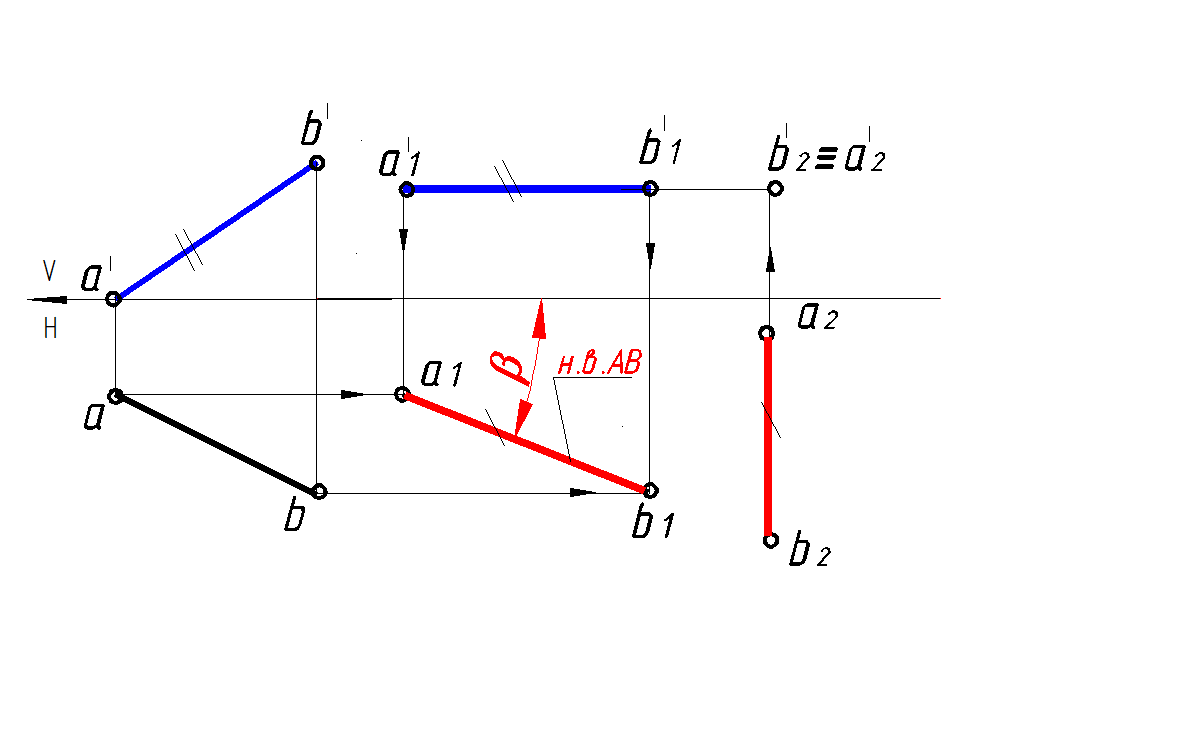
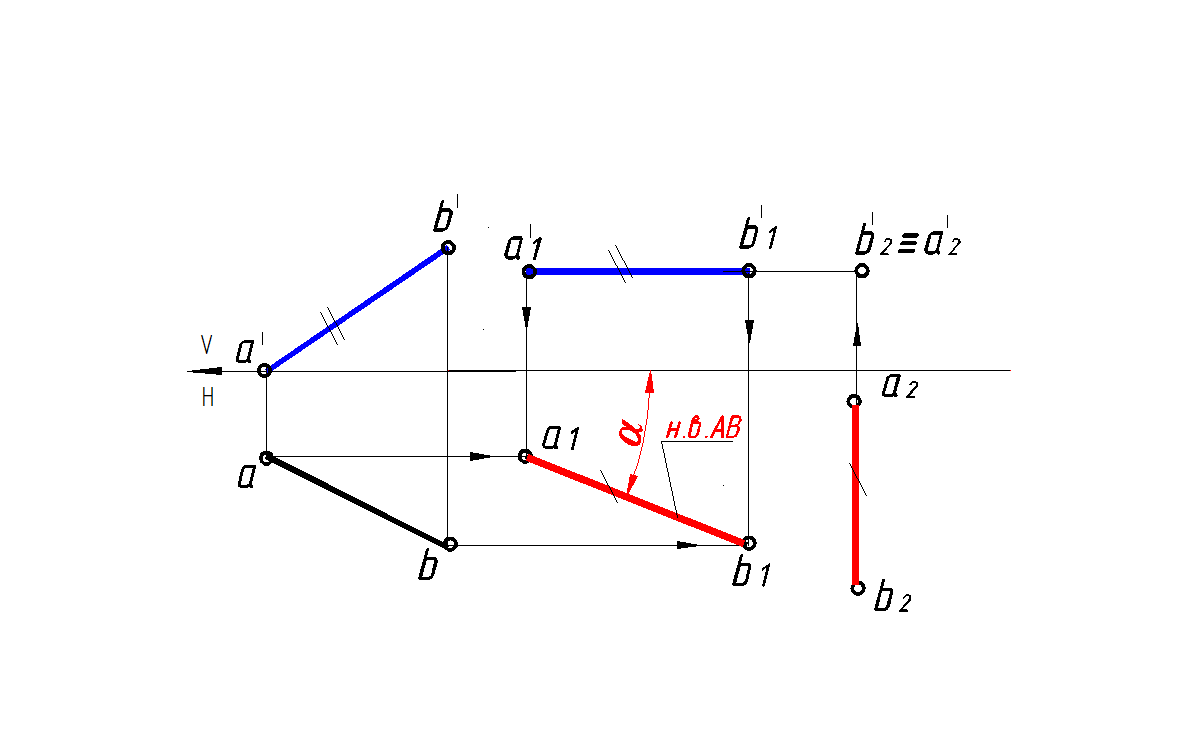
Рис. 113. Перевод отрезка из общего положения в проецирующее

                              способом плоскопараллельного перемещения

Рассмотрим другой пример – определение натуральной величины треугольника АВС общего положения (рис. 114).

Решение задачи состоит из двух последовательных перемещений треугольника в пространстве. Сначала треугольник (ABC) перемещается параллельно горизонтальной плоскости проекций так, что в конечном счете становится фронтально-проецирующей плоскостью. Для этого нужно его горизонтальную проекцию (a₁ b₁ c₁) на чертеже расположить так, чтобы горизонтальная проекция горизонтали а₁1₁ расположилась вертикально. Новая фронтальная проекция (а'₁b₁' c₁') вырождается в прямую линию.

Далее треугольник перемещается параллельно фронтальной плоскости, в результате чего будет параллелен горизонтальной плоскости проекций, а проекция ( a₂ b₂ c₂) определяет натуральную величину треугольника (ABC).

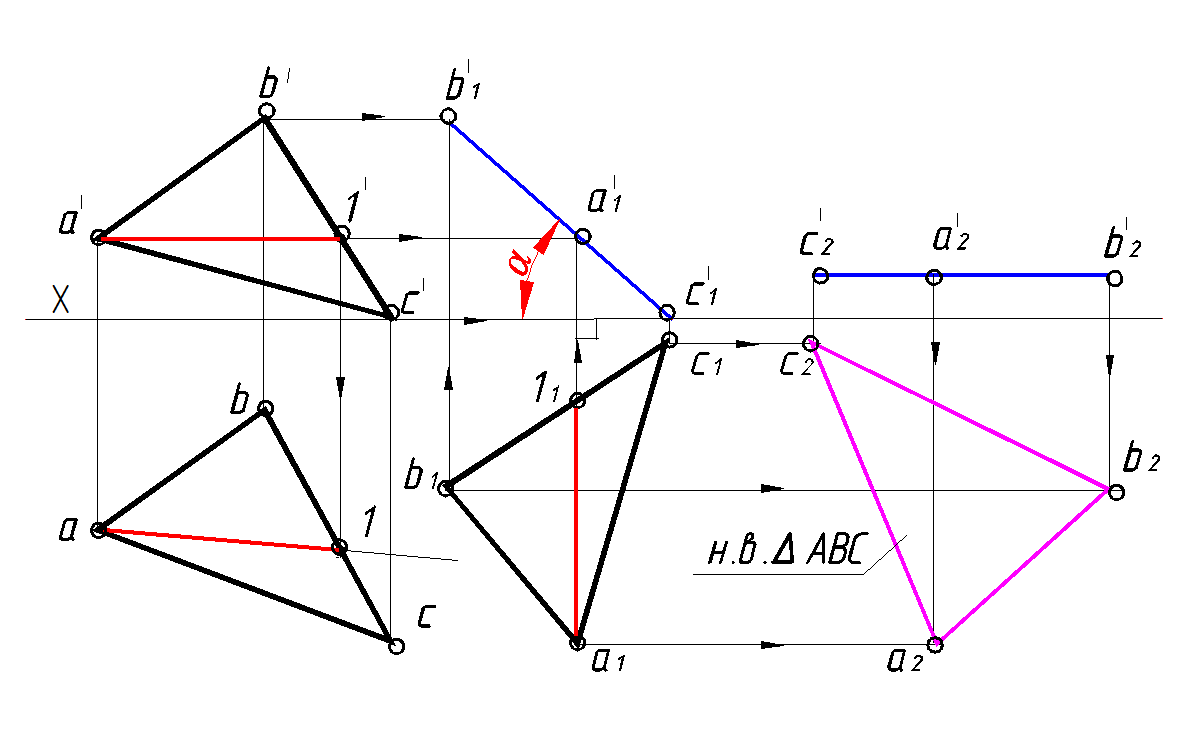
Рис. 114. Определение натуральной величины плоского треугольника

методом плоскопараллельного перемещения

Многогранники

Общие характеристики многогранников. Правильные многогранники (тела Платона). Изображение многогранников на чертеже. Пересечение многогранников плоскостью и прямой. Алгоритм решения задачи. Взаимное пересечение многогранников. Развертки: способ триангуляции, нормального сечения, раскатки.