Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней. Построение разверток – одна из интереснейших задач начертательной геометрии, имеющая большое значение в практике конструирования изделий из листового материала.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Существует три способа построения развертки многогранных поверхностей:
1) способ треугольников (триангуляция);
2) способ раскатки;
3) способ нормального сечения.
Рассмотрим построение разверток пирамид и призм, как наиболее распространенных в инженерной практике многогранников, этими способами.
1. Способ триангуляции
Это один из самых универсальных способов, при помощи которого можно построить развертку практически любой поверхности. Суть способа заключается в следующем. Вся поверхность разбивается на треугольники, определяется натуральная величина каждой стороны треугольника, и на плоскости строятся треугольники по трем сторонам один к другому. В результате этих построений получается развертка поверхности на плоскость.
Пример построения развертки треугольной пирамиды способом триангуляции показан на рис. 123. Основание пирамиды параллельно горизонтальной плоскости проекций и проецируется на нее без искажения (рис. 123, а). Ребро SA параллельно фронтальной плоскости проекций, и поэтому его фронтальная проекция выражает натуральную величину. Ребра SB и SC занимают общее положение. Их длину определяем методом вращения вокруг горизонтально-проецирующей оси, проходящей через вершину пирамиды S. После такого поворота эти ребра располагаются параллельно фронтальной плоскости проекций и проецируются на нее без искажения:
s ' b '1 = SB; s ' b '1 = SB .
Теперь известны величины всех ребер и сторон основания, и можно приступать к выполнению развертки (рис. 123, б). На плоскости чертежа по трем сторонам строится одна из граней, например, ASB. Затем к ней пристраиваются последовательно грани BSC , CSA и основание АВС.
Чтобы построить развертку поверхности призмы, надо ее боковые грани (четырехугольники) разбить диагоналями на треугольники, определить длины сторон этих треугольников, и построить последовательно треугольники в плоскости чертежа (рис. 124).
а б
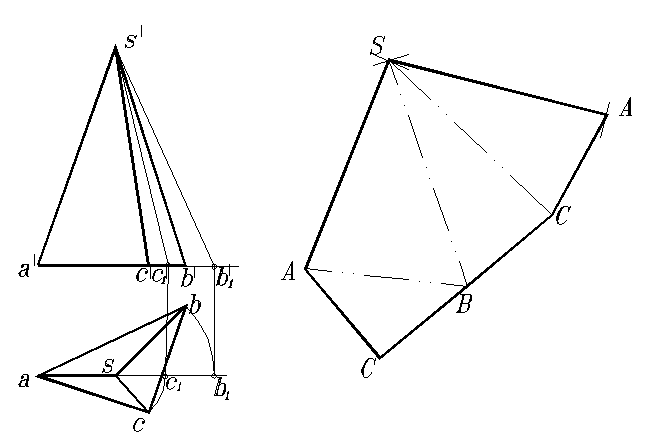
Рис. 123. Построение развертки пирамиды способом триангуляции
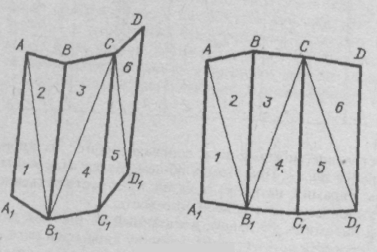
Рис. 124. Схема развертывания призматической поверхности
способом триангуляции
2. Способ раскатки
Этот способ целесообразно применять для построения развертки поверхностей призм – прямых или наклонных, когда основания призмы параллельны какой-либо плоскости проекций, а ребра параллельны другой плоскости проекций.
Суть способа заключается в следующем. Ребро призмы совмещается с плоскостью, и вращением вокруг него многогранник совмещается одной своей боковой гранью с плоскостью. Затем вращением вокруг второго ребра этой грани с плоскостью совмещается вторая грань, и так до полной развертки боковой поверхности.
Пример построения развертки наклонной треугольной призмы способом раскатки показан на рис. 125. Основания призмы параллельны горизонтальной плоскости проекций Н, ребра параллельны фронтальной плоскости проекций V.
Для построения развертки будем последовательно разворачивать грани призмы и совмещать их с фронтальной плоскостью проекций V. Все вершины призмы будут вращаться по окружностям в плоскостях, перпендикулярных плоскости V и ребрам призмы.
Осуществим поворот грани А DEB вокруг ребра AD. Зная натуральную величину сторон основания АВ и DE, устанавливаем натуральную величину этой грани, совмещенной с плоскостью V – a ' d ' E 0 B 0.
Затем принимаем совмещенное положение ребра В0 Е0 за ось, и вращаем вокруг нее следующую грань до совмещения ее с плоскостью развертки – E 0 B 0 C 0 F 0. Таким же образом совмещаем третью грань – A 0 D 0 C 0 F 0 .
Для получения полной развертки призмы достаточно к какому-либо из звеньев ломаной линии пристроить треугольники оснований А0 В0 С0 и D 0 E 0 F 0.
3. Способ нормального сечения
Этот способ применяется для построения разверток наклонных призм.
Сущность метода заключается в следующем. С помощью сечения призмы плоскостью, перпендикулярной боковым ребрам (нормального сечения), призма разделяется на две прямые призмы (рис. 126), основаниями которых является нормальное сечение. Определяется натуральная величина нормального сечения. Стороны этого сечения откладываются на горизонтальной прямой линии на плоскости развертки. Через концы сторон проводятся вертикальные прямые линии, на которых откладываются натуральные величины отрезков боковых ребер от нормального сечения до верхнего и нижнего оснований. Пристроенные верхнее и нижнее основания заканчивают построение полной развертки призмы.
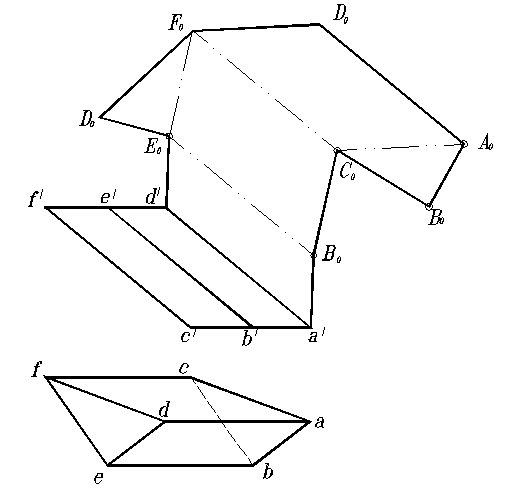
Рис. 125. Построение развертки призмы способом раскатки
а
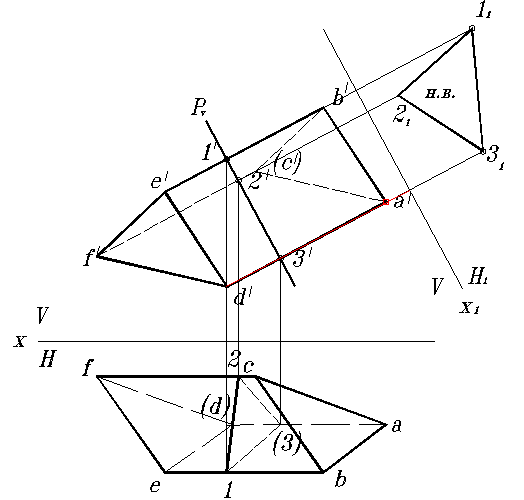
б
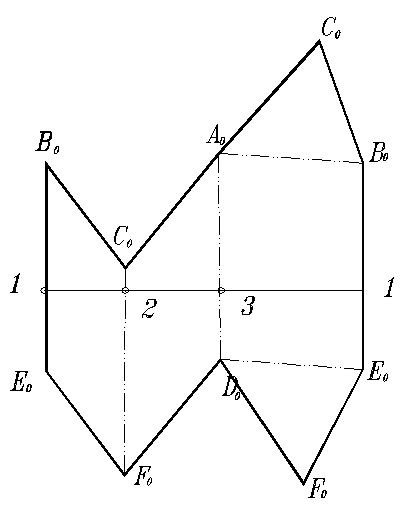
Рис. 126. Построение развертки призмы способом нормального сечения:
а- определение натуральной величины нормального сечения; б- развертка призмы
7. Кривые поверхности
Способы задания поверхностей. Понятие определителя поверхности. Классификация кривых поверхностей. Линейчатые поверхности. Нелинейчатые поверхности. Винтовые поверхности. Поверхности вращении. Особые линии на поверхностях вращения. Точка на поверхности. Поверхности вращения второго и четвертого порядка
Поверхности – это чрезвычайно обширный класс геометрических объектов. Исследования в области конструирования поверхностей привлекали внимание ученых древности, средневековья, и в наши дни актуальность этих исследований не уменьшилась. Г. Монж при исследовании кривых линий и поверхностей использовал дифференциальные уравнения.
В настоящее время для конструирования поверхностей и кривых линий применяется современный математический аппарат. Расчет и корректировка траекторий спутников и космических кораблей – сложнейшая геометрическая задача, решение которой без математического аппарата и вычислительной техники немыслимо.
Способы задания поверхностей
Определены три способа задания поверхностей: аналитический, каркасный, кинематический.
1. Аналитический способ применяют в математике.
Поверхность рассматривают как непрерывное множество точек, если между координатами точек этого множества может быть установлена зависимость, определяемая уравнением вида
F (x , y, z) = 0,
где F ( x , y, z) – многочлен п-й степени.
Если алгебраическая поверхность описывается уравнением п-й степени, то поверхность считается п-го порядка.
2. Кинематический способ.
Поверхность рассматривают как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии по определенному закону.
Для наглядности изображения поверхности закон перемещения целесообразно задавать графически семейством линий.
Линию, перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми. Кривые образующие могут быть постоянными и переменными.
Неподвижные линии называются направляющими.
Кроме того, должен быть указан характер движения образующей.
Например, при своем движении по направляющей l образующая а остается параллельной заданному направлению MN (рис. 127).
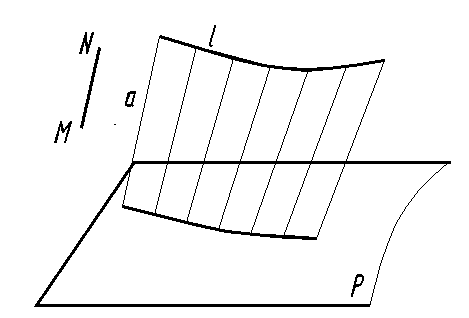
Рис. 127. Образование поверхности
3. Каркасный способ – поверхность рассматривают как множество точек или линий, принадлежащих ей.
Для того чтобы по каркасу можно было судить о форме поверхности, его следует задавать двумя семействами плоских сечений. Например, на рис. 128 показан каркас поверхности, состоящий из двух ортогонально расположенных семейств линий а1, а2, а3... ап и b1, b2, b3... bn . {b...}
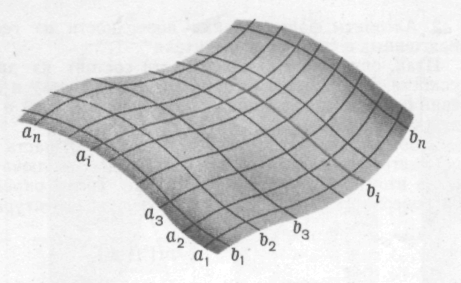
Рис. 128. Задание поверхности каркасом
При кинематическом способе задания поверхности необходимо прежде всего указать ее определитель – совокупность элементов, которые однозначно задают поверхность. Установив определитель, можно решать вопрос о принадлежности любой точки пространства к этой поверхности.
Определитель состоит из двух частей: геометрической (точки, линии, поверхности) и алгоритмической, устанавливающей связь между элементами поверхности.
Чтобы найти (установить) определитель поверхности, следует исходить из кинематического способа ее образования. Ввиду того, что поверхность может быть образована различным путем, то, очевидно, одна и та же поверхность может иметь различные определители.
Задать поверхность на чертеже – прежде всего, построить проекции определителя. Для придания изображению наглядности и выразительности вычерчивают еще очерк поверхности, наиболее важные линии и точки на поверхности.
Дата: 2018-11-18, просмотров: 1342.